Сопротивление проводников при поверхностном эффекте.

На поверхности возникает электрический ток:

Вследствие слабого проникновения поля в проводник, целесообразно ввести понятие поверхностной плотности тока как отношение всего тока, текущего по глубине, к единичной ширине проводника в направлении оси ОУ.

Поверхностная плотность тока

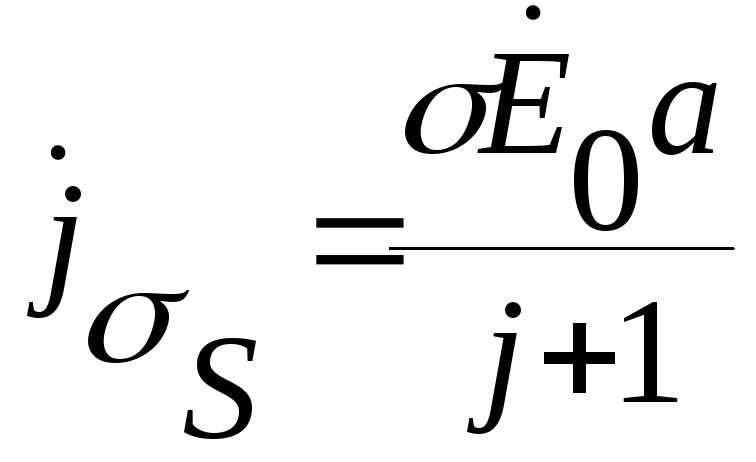
Удельное поверхностное сопротивление: ( оно комплексное, активная часть-реактивная, разность фаз ).

(индуктивный характер)

Найдём сопротивление проводника:

а мало, ,

(- сопротивление при постоянном токе)

При переменном токе сопротивление возрастает.

Иногда интересуются не глубиной проникновения, а величиной, при которой токи (поля) убывает в раз, (в условиях экранирования одной области от другой)

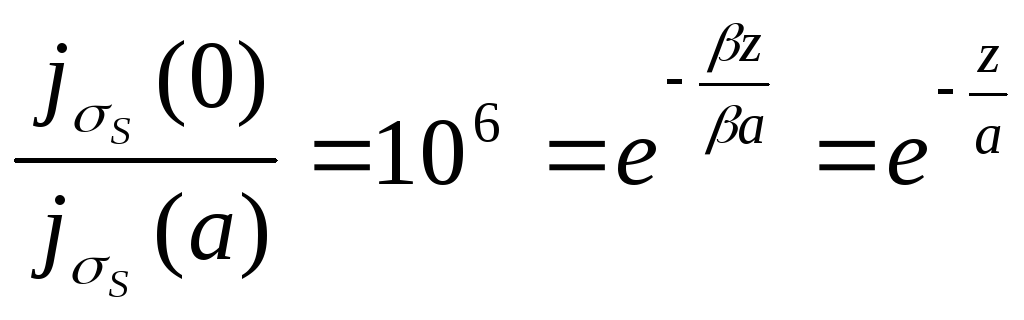
Явление слабого проникновения поля в проводнике существенно влияет на потери (при сверхвысоких частотах). Поэтому на них очень важна чистота обработки поверхности.

Если , то потери не увеличиваются по сравнению

с постоянным током

(их можно не учитывать)

Если , то существенно

возрастают потери (надо чистить до

зеркальной поверхности).

Вопрос 2.

Излучение:

С математической точки зрения необходимо найти векторный электродинамический потенциал.

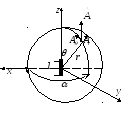
Для решения такой задачи нарисуем вибратор:

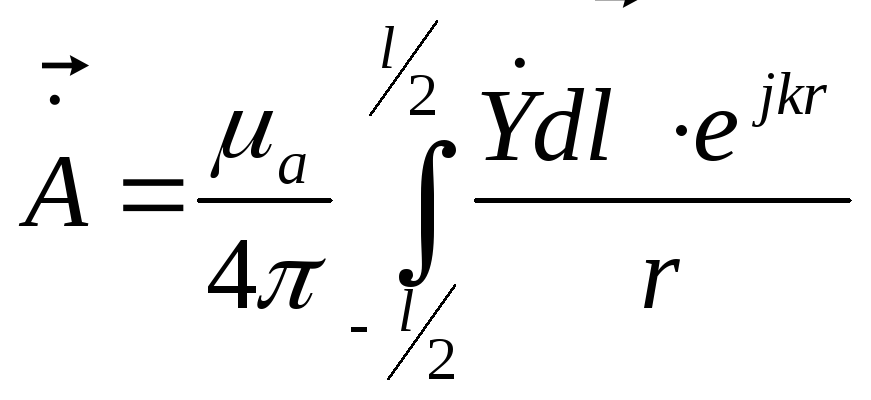
Потенциал будет иметь одну единственную составляющую по оси Z.

При условии под интегралом в знаменателе r практически меняться не будет.

Так как решаем в сферической системе координат, то целесообразно ввести сферические компоненты, составляющие векторного потенциала:

В полученных выражениях видно, что фаза поля одинакова на поверхности , следовательно, вибратор излучает сферические волны в окружающее пространство.

Зависимость поля от расстояния имеет сложный характер. На практике, в зависимости от интереса, где находиться поле, все окружающее пространство вокруг вибратора делят на зоны - ближнюю и дальнюю.

(В антенной технике – дальняя зона).

Выражения для поля в разных зонах существенно меняется.

• Поле в дальней зоне.

В общих выражениях для поля можно пренебречь слагаемыми, обратно пропорциональными высшим степеням r.

В дальней зоне поля синфазные.

СРЕДНЕЕ ЗА ПЕРИОД ЗНАЧЕНИЕ ВЕКТОРА УМОВА-ПОЙТИНГА.

Среднее за период значение вектора Умова-Пойтинга в течение всего времени направлено в сторону распространения энергии.

При фаза одинакова, следовательно, в дальней зоне электромагнитное поле имеет характер сферических волн.

Амплитуды поля этих волн убывают с расстоянием сравнительно слабо.

Амплитуды поля дальней зоны связаны между собой простым соотношением: .

В дальней зоне около наблюдателя поле имеет характер плоских волн.

Амплитуда поля обратно пропорционально длине волны, медленно меняющиеся во времени токи и заряды (с низкой частотой) непригодны для антенного излучения.

№34

1. Понятие поляризации электромагнитного поля

В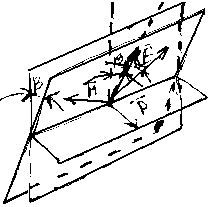ажным показателем э/м поля является поляризация – характеризует направление вектора электрического поля относительно плоскости распространения волн. Определяет закон изменения направления вектора Е в данной точке за период колебаний. Плоскость, в которой E,P называется плоскостью поляризации. Угол α между плоскостью поляризации и плоскостью распространения волн называется углом поляризации. Различают несколько видов поляризации э/м волн. В зависимости от ориентации векторов E,H. Если E лежит в плоскости распространения S (вертикальная плоскость, в которой лежит вектор умова-пойнтинга), a H перпендикулярен этой плоскости, то независимо от того есть ли наклон фронта волны или нет принято считать поляризацию вертикальной, при этом плоскость поляризации совпадает с плоскостью распространения. Если H лежит в плоскости распространения, а Е перпендикулярен этой плоскости, то поляризация называется горизонтальной. В случае, если Е занимает произвольное положение, то он может быть представлен в виде 2х составляющих. 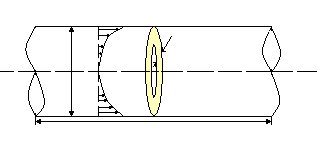Вертикальная составляющая Eв(вектор) лежит в плоскости распространения S, а Eг(в) в перпендикулярной плоскости к S и параллельно горизонту. На рисунке представлен случай одновременного наклона фронта волны (угол β) и поворота плоскости поляризации (угол α). β,α – в разных плоскостях. если вертикальные и горизонтальные составляющие вектора E равны по амплитуде, отличаются по фазе на 90°, то поляризация имеет круговой характер. Во всех других случаях поляризация будет элептической. На рисунке - поворот плоскости поляризации, когда фронт волны наклонен на угол β.

2. Излучение. Поле элементарного электрического вибратора.

Электромагнитное поле создаётся в виде электромагнитных волн, излучающих переменными во времени зарядами и электрическими токами. Для нахождения электромагнитного поля необходимо решать неоднородные уравнения электродинамики, т.е. при наличии сторонних токов и зарядов. При наличие сторонних токов и зарядов уравнение электродинамики сводятся к неоднородным волновым уравнениям.

Проще для задач записывать это уравнения для электродинамических потенциалов:

Решение этих уравнений (частные) для безграничного пространства.

Для нахождения электромагнитного поля необходимо решить эти волновые уравнения.

Через потенциал выразим поле:

Если поле находиться вне зарядов и токов, то Е:

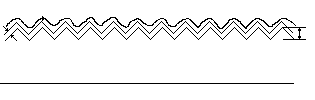
Элементарный электрический вибратор-отрезок проводника с электрическим током, размеры которого малы по сравнению с волной, а распределение тока по которому является равномерным.

Такое понятие идеализировано:

Такой вибратор можно создать физически:

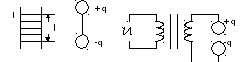
С математической точки зрения необходимо найти векторный электродинамический потенциал.

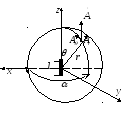
Для решения такой задачи нарисуем вибратор:

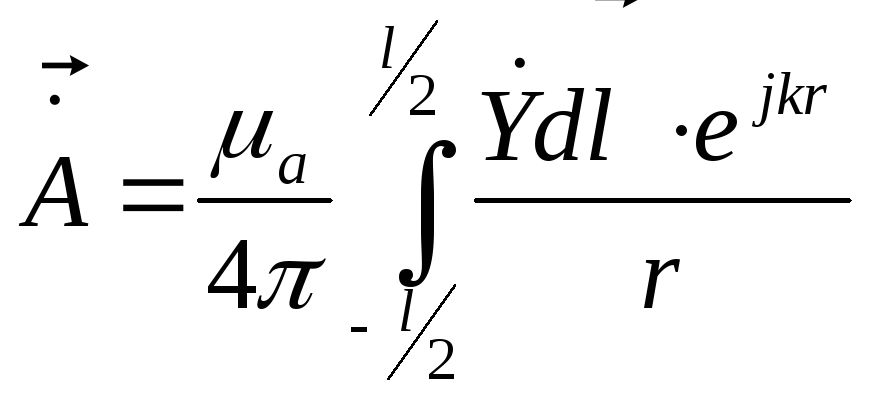
Потенциал будет иметь одну единственную составляющую по оси Z.

При условии под интегралом в знаменателе r практически меняться не будет.

Так как решаем в сферической системе координат, то целесообразно ввести сферические компоненты, составляющие векторного потенциала:

В полученных выражениях видно, что фаза поля одинакова на поверхности , следовательно, вибратор излучает сферические волны в окружающее пространство.

Зависимость поля от расстояния имеет сложный характер. На практике, в зависимости от интереса, где находиться поле, все окружающее пространство вокруг вибратора делят на зоны - ближнюю и дальнюю.

(В антенной технике – дальняя зона).

Выражения для поля в разных зонах существенно меняется.

№35

1. Плоская волна, распространяющаяся в произвольном направлении

Получим уравнение плоской волны, распространяющейся в направлении, образующем с осями координат х, у, z углы α,β, γ Пусть колебания в плоскости, проходящей через начало координат, имеют вид .

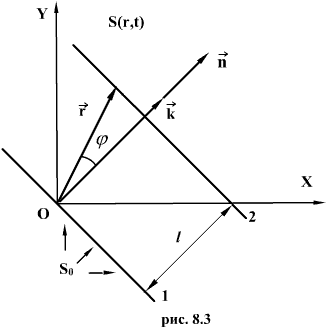
Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l. Колебания в этой плоскости будут отставать от колебаний в точке О (рис.8.3) на время тогда уравнение волны

(8.4)

Выразим расстояние l через радиус-вектор точек рассматриваемой поверхности. Для этого введем единичный вектор нормали к волновой поверхности. Скалярное произведение

Подставим значение l в уравнение (8.4) и внесем в скобки

Отношение равно волновому числу k. Вектор равный по модулю волновому числу и имеющий направление вдоль нормали к волновой поверхности называется волновым вектором. Введя вектор , получим

(8.5)

Чтобы перейти от радиуса - вектора точки к ее координатам х, у, z , выразим скалярное произведение через проекции векторов на координатные оси :

Тогда уравнение плоской волны принимает вид:

(8.6)

Где

2. Особенности поля элементарного вибратора в ближней зоне

В общих выражениях для поля можно пренебречь слагаемыми, обратно пропорциональными низшим степеням r.

Из них видно, что амплитуды поля чрезвычайно быстро убывают с расстоянием. Электрическое и магнитное поля сдвинуты относительно друг друга на 90⁰.