2.2. Дельта - функция - как пример пробного сигнала.

Для анализа прохождения сигналов через электрические цели широко используются пробные сигналы, обладающие какими - либо характерными свойствами. Такой функцией, в частности, является дельта-функция (t), обращающаяся в ноль при t0 и в бесконечность при t=0, так, что

(3).

Этому определению удовлетворяет, например, прямоугольный импульс длительностью t_u , амплитуда которого обратно пропорциональна его длительности 1/t_u . При t_u0 амплитуда импульса бесконечно растет, а площадь остается постоянной - равной единице. Действительно, если

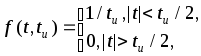
то дельта-функцию можно определить как (t)=

При этом

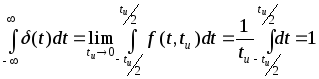
В более общем случае дельта-функцию можно записать в виде

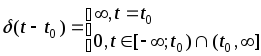(4)

Спектральную плотность дельта-импульса A(t) найдем с помощью прямого преобразования Фурье :

(5)

На основании определения дельта-функции интервал интегрирования в формуле (5) можно сделать сколь угодно малым, лишь бы он включал в себя момент t=0. В пределе он может быть устремлен к нулю и подъинтегральная функция e^jt примет значение, равное единице. Таким образом . Следовательно, спектральная плотность дельта-импульса имеет равномерный частотный спектр. ФЧХ дельта-импульса равна нулю для всех частот. Это означает, что все гармонические составляющие начинаются с одной фазы и образуют бесконечный пик при t=0.

По определению, дельта-функция обладает свойством, которое может быть выражено соотношением

(6)

Его называют фильтрующим свойством дельта-функции, согласно которому интеграл от произведения произвольной функции на (t-t₀) равен значению этой функции в точке t=t₀ .

На основании обратного преобразования Фурье выразим дельта-функцию через ее спектр :

(t)= (7)

По аналогии с (7) можно ввести дельта-функцию аргумента 

()= (8)

В (8) знак показателя экспоненты не влияет на значение интеграла, поскольку и независимо от знака интеграл от нечетной функции sin на симметричном интервале интегрирования равен нулю. Поэтому можно записать

()= (9)

2.3. Временной и спектральный методы анализа передачи сигналов через линейные цепи.

Пусть на вход линейной стационарной цепи подан сигнал S_вх(t). На основании определений дельта-функции и ее фильтрующего свойства входной сигнал может быть представлен в виде интеграла

S_вх(t)= (10)

поскольку он является предельным выражением суммы, которой входной сигнал представляется как бесконечная последовательность дельта- импульсов, смешенных друг относительно друга на время . Амплитуда импульсов равна значению сигнала в те же моменты времени  (см. рис.)

Такой метод аналитического моделирования сигналов называется ме- тодом интеграла наложения ( на последовательность пробных импульсов накладывается информац. сигнал).

Если установить реакцию цепи на отдельный дельта-импульс, то в силу линейности и стационарности цепи можно просуммировать отдельные реакции и получить выходной отклик на любое входное воздействие. Поэтому вводят импульсную характеристику цепи h(t), являющуюся выходным откликом на входной дельта-импульс. Таким образом, выходная реакция S_вых(t) на произвольное входное воздействие может быть представлена интегралом

S_вых(t)= (11)

Из (11) следует, что сигнал на выходе цепи S_вых(t) в момент t получается суммированием мгновенных значений входного сигнала S_вх(t) с весом h(t-) за все предыдущее время с начала сигнала. Импульсная характеристика и метод интеграла наложения являются основными понятиями при исследовании прохождения сигналов через линейные цепи методом интеграла наложения.

Соотношение (11) может быть записано также в виде

S_вых(t)= (12)

Представим входной сигнал в виде интеграла Фурье

S_вх(t)=

Если сделать подстановку t=t^’- (а потом отбросить штрих у t ), то можно записать, что

S_вх(t-)=

Подставив это выражение в (12) и изменив порядок интегрирования, получим

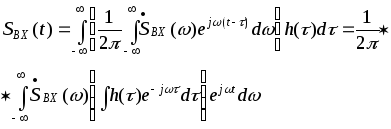(13)

Внутренний интеграл является комплексной функцией частоты. Обозначим его как

 (14)

является прямым преобразованием Фурье для импульсной функции цепи. Его функции называют частотным коэффициентом передачи цепи (или комплексной частотной характеристикой).

Частотному коэффициенту передачи можно дать и другие эквивалентные толкования. Одно из них получается в результате подстановки (14) в (13) :

S_вых(t)= (15)

Как видно, полученное выражение совпадает с обратным преобразованием Фурье для спектра выходного сигнала, поскольку

_ВЫХ(), (16)

или, другими словами, частотный коэффициент передачи есть множитель пропорциональности между спектральными плотностями входного и выходного сигналов. Отсюда возникло название метода анализа прохождения сигналов через линейные цепи, основанного на использовании частотного коэффициента передачи, как спектрального метода.

Практически частотный коэффициент передачи удобнее вычислять пользуясь другим его определением. Для этого рассмотрим в качестве входного сигнала гармоническое колебание в комплексной форме : S_ВХ(t)=. Гармоническое колебание, сдвинутое во времени S_BX(t-)=. Подставив это выражение в (12), выносят из под интеграла функции, не зависящие от переменной интегрирования и перегруппировав члены, получим :

S_ВХ(t)=.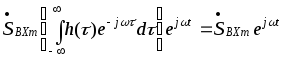

Здесь интеграл есть частотный коэффициент передачи. Таким образом, _ВЫХm , откуда

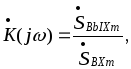(17)

и, следовательно, коэффициент передачи равен отношению комплексных амплитуд гармонических колебаний на выходе и входе линейной цепи. Частотный коэффициент передачи обычно записывают в показательной форме

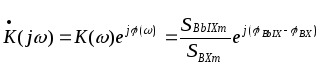(18)

где K()=|| - амплитудно-частотная характеристика цепи (АЧХ) ()=_вых-_вх - фазочастотная характеристика цепи (ФЧХ).

Из соотношения (12) следует еще один метод практического определения импульсной характеристики h() :

(19)

где  - время анализа, - скорость изменения выходного сигнала в течении времени анализа , - значения входного сигнала в течении времени анализа .

Таким образом, импульсная характеристика характеризует скорость изменения выходного сигнала за время анализа по отношению к мгновенным значениям входного сигнала в течении этого же интервала времени. Для ее определения достаточно знать форму входного и выходного сигналов за время действия пробного сигнала. Отсюда понятно и введение понятия пробного сигнала.

Л 13.