
- •1.Производная функции. Ее физический и геометрический смысл.
- •2.Описание скорости протекания биологических процессов с помощью производной. Градиенты.
- •3.Производные высших порядков. Частные производные.
- •4.Применение производных для исследования функций на экстремум.
- •5.Дифференциал функции, его геометрический и физический смысл.
- •7.Состояние организма как функция многих переменных. Приближенные значения.
- •8.Нахождение частных производных и полного дифференциала.
- •9.Первообразная функции и неопределенный интеграл. Интегрирование.
- •10.Методы нахождения неопределенных интегралов: Приведение к табличному виду и метод замены переменной (интегрирование по частям).
- •Используя формулу (1), получаем
- •11.Определенный интеграл, его применение для вычисления площадей фигур и работы переменной силы.
- •12.Вычисление определенных интегралов, правило Ньютона – Лейбница.
- •14.Дифференциальные уравнения. Простейшие приемы составления и решения дифференциальных уравнений.
- •15.Понятие об обыкновенных дифференциальных уравнениях. Решение дифференциальных уравнений с разделяющимися переменными.
- •16.Решение дифференциальных уравнений. Общие и частные решения.
- •18.Вероятностный характер медико – биологических процессов. Элементы теории вероятностей.
- •19.Вероятность случайного события. Закон сложения вероятностей.
- •20.Вероятность случайного события. Закон умножения вероятностей.
- •22.Элементы математической статистики. Случайная величина.
- •23. Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение. (часть 1)
- •23. Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение. (часть2).
- •24.Примеры различных законов распределения. Нормальный закон распределения.(часть 1).
- •24.Примеры различных законов распределения. Нормальный закон распределения.(часть 2)
- •24.Примеры различных законов распределения. Нормальный закон распределения.(часть 3)
- •25. Генеральная совокупность и выборка. Гистограмма.
- •30.Понятие о корреляционном анализе.
- •31.Упругие, вязкие и вязкоупругие среды, их механические характеристики и модели.
- •32.Механические свойства костной ткани, мыщц, сухожилий и сосудов.
- •33.Механические колебания: гармонические.
- •Дифференциальное уравнение гармонического колебания.
- •34. Механические колебания: затухающие (часть 1).
- •34. Механические колебания: затухающие.(часть 2)
- •35.Механические колебания: вынужденные.
- •36.Резонанс. Автоколебания.
- •37. Энергия гармонических колебаний.
- •38.Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных. (часть1).
- •38.Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных.(часть 2).
- •Сложение взаимно-перпендикулярных колебаний.
- •39. Механические волны, их виды и скорость распространения. Уравнение волны. Энергетические характеристики волны. (часть1).
- •Уравнение волны.
- •39. Механические волны, их виды и скорость распространения. Уравнение волны. Энергетические характеристики волны.(часть 2)
- •40.Эффект Доплера и его применение для неинвазивного измерения скорости кровотока.
- •41.Акустика.Физические характеристики звука..Характеристика слухового ощущения и их связь с физическими характеристиками звука.
- •42.Вебера-Фехнера. Уровни интенсивности и уровни громкости звука. Единицы их измерения - децибелы и фоны.
- •43.Аудиометрия. Фонокардиогра фия.
- •44. Поглощение и отражение акустических волн. Акустический импеданс.
- •45. Ультразвук. Методы получения и регистрации. Действие ультразвука на вещество.
- •46. Биофизические основы действия ультразвука на клетки и ткани организма.
- •47. Ультразвуковая диагностика. Принципы ультразвуковой томографии.
- •48. Инфразвук. Биофизические основы действия инфразвука на биологические объекты.
- •49. Сущность физического явления поверхностного натяжения. Коэффициент поверхностного натяжения и методы его определения.
- •50. Капиллярные явления, их значение в биологических системах. Газовая эмболия.
- •51. Основные понятия гидродинамики. Условие неразрывности струи. Уравнение Бернулли.
- •1. Схема трубки тока жидкости для вывода формулы Бернулли.
- •1)Наклонная трубка тока постоянного сечения.
- •2)Горизонтальная трубка тока переменного сечения.
- •52. Внутреннее трение (вязкость) жидкости. Ньютоновские и неньютоновские жидкости Реологические свойства крови, плазмы, сыворотки. Факторы, влияющие на вязкость крови в живом организме.
- •53. Течение вязкой жидкости. Формула Пуазейля.
- •54. Гидравлическое сопротивление. Распределение давления и скорости крови в сосудистой системе.
- •55. Применение уравнения Бернулли для исследования кровотока в крупных артериях и аорте (закупорка артерии, артериальный шум, поведение аневризмы).
- •5) Разрыв аневризмы.
- •56. Распределение скорости кровотока и кровяного давления в большом круге кровообращения. Особенности течения крови по крупным и мелким кровеносным сосудам.
- •57. Методы определения давления и скорости крови. Физичес кие принципы определения давления и скорости движения крови.
- •58. Ламинарное и турбулентное течение. Число Рейнольдса. Условия проявления турбулентности в системе кровообращения.
- •59. Роль эластичности кровеносных сосудов в системе кровообращения. Пульсовая волна. Скорость распространения пульсовой волны.
- •9.2. Пульсовая волна
- •60. Работа и мощность сердца, их количественная оценка.
- •61. Методы определения вязкости: Стокса, Оствальда, ротационный метод.
- •2.Метод падающего шарика (метод Стокса).
- •62. Устройство вискозиметра Оствальда. Определение с его помощью вязкости исследуемой жидкости.
- •63. Физические вопросы строения и функционирования мембран. Транспорт веществ через мембраны.
- •64. Пассивный транспорт. Простая и облегченная диффузия. Математическое описание пассивного транспорта.
- •65. Активный транспорт ионов. Механизм активного транспорта на примере натрий-калиевого насоса.
- •66. Мембранные потенциалы и их ионная природа. Потенциал покоя.
- •67. Мембранные потенциалы и их ионная природа. Уравнение Нернста. Уравнение Гольдмана-Ходжкина-Катца.
- •68. Механизм генерации потенциала действия. Распространение потенциала действия по миелиновым и безмиелиновым нервным волокнам.
- •69. Общие характеристики датчиков температуры. Зависимость сопротивления металлов и полупроводников от температуры.
- •70. Контактная разность потенциалов. Градуировка термопары, термистора и проволочного терморезистора.
- •71. Усилители. Коэффициент усиления усилителя. Требования к усилителям. Многокаскадное усиление. Классификация усилителей.
- •72. Амплитудная характеристика усилителя. Амплитудные искажения. Предупреждение амплитудных искажений.
- •73. Частотная характеристика усилителя. Частотные искажения. Полоса пропускания усилителя. Предупреждение частотных искажений.
- •74. Усилительный каскад на транзисторе. Обратная связь в усилителях. Виды обратной связи.
- •75. Повторители. Назначение и типы повторителей.Дифференциальный усилитель.
- •75. Повторители. Назначение и типы повторителей.Дифференциальный усилитель.
- •77. Первичные механизмы воздействия электростатических полей на биологические объекты. Применение постоянных электрических полей в физиотерапии.
- •78. Физические основы электрографии тканей и органов. Электрокардиография. Диполь ный эквивалентный электрический генератор сердца. Теория отведений Эйнтховена.
- •79. Понятие о мультипольном эквивалентном электрическом генераторе сердца. Электрокардиограф.
- •80. Электропроводность биологических тканей и жидкостей для постоянного тока.
- •81. Первичные механизмы действия постоянного тока на жи вую ткань. Гальванизация. Лечебный электрофорез.
- •82. Переменный ток. Различные виды электрических сопротивлений в цепи переменного тока. Импеданс.
- •83. Сопротивление живой ткани переменному току, его зависимость от частоты тока.
- •14.2. Переменный ток
- •84. Эквивалентная электрическая схема живой ткани. Электрические фильтры.
- •85.Основные характеристики магнитного поля. Магнитные свойства веществ. Магнитные свойства биологических тканей.
- •86.Первичные механизмы воздействия магнитных полей на организм. Терапевтическое использование магнитных полей. Аппарат терапии переменным магнитным полем
- •87.Электростимуляция тканей и органов. Параметры импульсного сигнала и их физиологическое значение.
- •88. Связь амплитуды, формы импульса, частоты следования импульсов, длительности импульсного сигнала с раздражающим действием импульсного тока. Закон Дюбуа-Реймона.
- •89. Связь амплитуды, формы импульса, частоты следования импульсов, длительности импульсного сигнала с раздражающим действием импульсного тока. Уравнение Вейса-Лапика.
- •90.Аппаратура для электростимуляции. Примеры использования электростимуляции в клинике. Электростимуляция сердца и ее виды.
- •91.Воздействие переменными токами.
- •92. К физиотерапевтическим аппаратам высокочастотной терапии относятся аппараты электрохирургии, диатермии, местной дарсонвализации, индуктотермии, увч-терапии, микроволновой терапии.
- •Аппарат электрохирургии высокочастотный
- •Терапевтический контур
- •1. Явление рефракции
- •2. Отражение и преломление света.
- •3.Понятие о предельном угле падения и предельном угле преломления
- •4.Удельная рефракция вещества
- •5.Молекулярная рефракция вещества
- •94.Устройство и принцип действия рефрактометра.
- •95. Волоконная оптика и ее использование в оптических устройствах
- •96. Ход лучей в микроскопе. Увеличение и предел разрешения оптических микроскопов.
- •1. Микроскоп. Формула для увеличения
- •97. Формула Аббе. Значение апертурного угла. Ультрафиолетовый микроскоп. Иммерсионные системы. Полезное увеличение. Специальные приемы микроскопии.
- •98. Основы электронной микроскопии.
- •100. Тепловое излучение тел. Законы Кирхгофа.
- •101. Тепловое излучение тел. Стефана-Больцмана.
- •102. Тепловое излучение тел. Вина.
- •103. Тепловое излучение тел. Формула Планка.
- •104. Законы теплового излучения, область их применения. Использование тепловидения и термографии в медицине.
- •105. Электромагнитные волны, шкала электромагнитных волн. Интерференция света.
- •Вся шкала условно подразделена на шесть диапазонов: радиоволны (длинные, средние и короткие), инфракрасные, видимые, ультрафиолетовые, рентгеновские волны и гамма-излучение.
- •106. Электромагнитные волны, шкала электромагнитных волн. Дифракция света.
- •Вся шкала условно подразделена на шесть диапазонов: радиоволны (длинные, средние и короткие), инфракрасные, видимые, ультрафиолетовые, рентгеновские волны и гамма-излучение.
- •107. Интерференционные и дифракционные прибо ры. Принцип рентгеноструктурного анализа.
- •108. Понятие о голографии.
- •109. Поляризация света. Поляризационные методы исследования биологи ческих объектов.
- •110. Поляриметрия и спектрополяриметрия. Поляризационные приборы.
- •111. Излучение и поглощение энергии атомами. Структура энергети ческих уровней атомов. Оптические спектры атома водорода и спектры сложных атомов.
- •112. Структура энергетических уровней сложных молекул. Молекулярные спектры.
- •113. Эмиссионный и абсорбционный спектральный анализ, его медицинс кое применение.
- •114. Спектроскопы, спектрографы, монохроматоры, спектро фотометры и их применение в медицине.
- •115. Люминесценция, ее виды. Характеристики люминесценции (спектр, длительность, квантовый выход). Законы Вавилова и Стокса.
- •116. Люминесцентный анализ. Люминесцентные метки и зонды. Медицинское применение люминесцентных методов исследования.
- •117. Поглощение света и его законы. Показатель поглощения, коэффи циент пропускания, оптическая плотность.
- •118. Регистрация спектров поглоще ния биологических объектов. Фотоколориметрия и спектрофотометрия.
- •119. Рассеяние света. Нефелометрия.
- •120. Вынужденное излучение, его особенности. Условия усиления света.
- •121. Оптические квантовые генераторы (лазеры). Характеристики лазерного излучения.
- •122. Воздействие низкоинтенсивного и высокоинтенсивного лазерного излучения на биологические ткани. Физические основы лазерной терапии и хирургии.
- •123. Электронный парамагнитный резонанс (эпр). Идентификация и определение концентрации свободных радикалов методами эпр.
- •124. Ядерный магнитный резонанс (ямр). Принципы и диагностические возможности магнито-резонансной томографии (мрт).
- •125. Рентгеновское излучение, его природа. Тормозное рентгеновское излучение.
- •126. Рентгеновское излучение, его природа. Характерис тическое рентгеновское излучение.
- •127. Взаимодействие рентгеновского излучения с веществом. Слой половинного ослабления. Защита от рентгеновского излучения.
- •128. Физические принципы рентгенодиагностики и рент генотерапии. Понятие о рентгеновской компьютерной томографии.
- •129. Основные характеристики ядер атомов. Радиоактивный распад. Виды распада.
- •130. Спектры альфа-, бета- и гам ма-излучений. Основной закон радиоактивного распада.
- •131. Период полураспада. Активность и единицы активности. Методы получения радионуклидов.
- •132. Взаимодействие ионизирующего излучения с веществом. Линейная плотность ионизации, линейная передача энергии, средний пробег ионизирующей частицы.
- •Величина лпэ в кэВ/мкм зависит от плотности вещества.
- •133. Особенности взаимодействия с веществом альфа-, бета-, гамма-излучений и нейтронов.
- •134. Физические принципы защиты от ионизирующих из лучений. Понятие об основных биологических эффектах ионизирующих из лучений.
- •135. Физические основы радионуклидных методов диагностики и лучевой терапии.
- •135/1. Использование радионуклидов и нейтронов в медицине
- •136. Дозиметрия ионизирующего излучения. Поглощенная, экспозицион ная и эквивалентная дозы. Единицы их измерения.
- •137. Мощность дозы. Связь мощности дозы с активностью. Эффективная эквивалентная доза. Коллек тивная доза.
- •138. Связь между активностью и эквивалентной дозой внутреннего облу чения. Принципы расчета эквивалентной дозы внутреннего облучения.
- •139. Методы регистрации ионизирующих излучений, дозиметрические и радио метрические приборы. Естественный радиационный фон. Техногенный фон.
- •139/1. Методы регистрации излучений. Приборы. Естеств. И техног. Радиац. Фон
15.Понятие об обыкновенных дифференциальных уравнениях. Решение дифференциальных уравнений с разделяющимися переменными.
Дифференциальным называют уравнение, связывающее аргумент х, искомую функцию у = f(x), ее производные f(x), f(x), …, f(п)(x) или дифференциалы df, d2f, …, dпf.
Дифференциальное уравнение в общем виде можно записать так:
F(x, f(x), f(x), f(x), …, f(п)(x)) = 0
Если искомая функция y = f(x) есть функция одного аргумента, то дифференциальное уравнение называют обыкновенным.
Уравнение вида f1(x)1(y)dx + f2(x)2(y)dx =0
называется уравнением с разделяющимися переменными. Оно может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на 1(y) f2(x):
![]()
при условии, что 1(y) f2(x) 0. После сокращения получаем
![]() (1)
(1)
Интегрируя равенство (1), получаем
![]() (2)
(2)
где С – произвольная постоянная.
Выражение (2) является общим решением уравнения (1).
Пример. Найти общее и частное решения уравнения dy/dx = - y/x при x = 1, y = 2.
Решение.
В уравнении
dy/dx
= - y/x
путем
умножения обеих частей на dx
разделим (отделим) дифференциалы:
dy
= -( y/x)dx.
Разделив
обе части последнего уравнения на у,
получим уравнение с разделенными
переменными: dy/у
= -dx/x.
Проинтегрируем
его:
![]() откуда
откуда
![]()
Потенцируя
последнее равенство, получаем
![]() -
общее решение уравнения. Из
условия, что при х
= 1 у = 2, найдем
значение С:
2 = С/1,
откуда С = 2.
Частное решение будет иметь вид у
= 2/х.
-
общее решение уравнения. Из
условия, что при х
= 1 у = 2, найдем
значение С:
2 = С/1,
откуда С = 2.
Частное решение будет иметь вид у
= 2/х.
16.Решение дифференциальных уравнений. Общие и частные решения.
Дифференциальным называют уравнение, связывающее аргумент х, искомую функцию у = f(x), ее производные f(x), f(x), …, f(п)(x) или дифференциалы df, d2f, …, dпf.
Дифференциальное уравнение в общем виде можно записать так:
F(x, f(x), f(x), f(x), …, f(п)(x)) = 0
Если искомая функция y = f(x) есть функция одного аргумента, то дифференциальное уравнение называют обыкновенным.
Если
функция u
= f(x,
y,
z,
…, t)
зависит от
двух и большего числа аргументов, то
уравнение будет содержать частные
производные
![]() и
т.д. Такое уравнение носит названиедифференциального
уравнения в частных производных.
и
т.д. Такое уравнение носит названиедифференциального
уравнения в частных производных.
Порядком дифференциального уравнения называется порядок наивысшей производной или дифференциала, входящих в уравнение.
Например, у = 2ху2 + 5 – уравнение первого порядка, а у + у =0 – второго.
Общим решением дифференциального уравнения порядка r называется функция y = f(x,C1, C2, …, Cr) от х с произвольными постоянными C1, C2, …, Cr,обращающая это уравнение в тождество. Общее решение, записанное в неявном виде Ф(x, у,C1, …, Cr) = 0, называется общим интегралом.
Так, решением дифференциального уравнения у + у =0 является функция у = С1 sin x + C2 cos x, где C1 и C2 – произвольные постоянные. При подстановке функции у = С1 sin x + C2 cos x в уравнение у + у =0 оно превращается в тождество. Действительно, ух = C1 cos x – С2 sin x; ухх = - С1 sin x - C2 cos x;
- С1 sin x - C2 cos x + С1 sin x + C2 cos x =0.
При любом наборе конкретных постоянных получаются частные решения. На практике частное решение получают из общего не прямым заданием значений произвольных постоянных, а с учетом тех условий, которым должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий и записывается кратко так:
f(x0) = y0; f(x0) = y0;…; f(r-1)(x0) = y0(r-1). Задача нахождения частного решения, удовлетворяющего начальным условиям, называется задачей Коши.
17. Моделирование медико-биологических процессов с помощью дифференциальных уравнений (развитие эпидемий, изменение со временем концентрации лекарственных веществ в организме, накопление и выведение радионуклидов и др.).
Общие замечания. Дифференциальные уравнения занимают важное место в решении задач физико-химического, фармацевтического и медико-биологического содержания. Пользуясь ими, мы устанавливаем связь между переменными величинами, характеризующими данный процесс или явление.
Решение любой задачи с помощью математического анализа можно разбить на три этапа:
1.перевод условий задачи на язык математики;
2.решение задачи;
3.оценка результатов.
Первая часть работы обычно заключается в составлении дифференциального уравнения и является наиболее трудной, так как общих методов составления дифференциальных уравнений нет и навыки в этой области могут быть приобретены лишь в результате изучения конкретных примеров.
Закон охлаждения тела. Согласно закону Ньютона, скорость охлаждения тела пропорциональна разности между температурами тела и окружающей среды. Пусть тело нагрето до температуры То, температуру окружающей среды будем считать постоянной и равной Тс, Тс < То. В момент времени t температура тела равна Т. Скорость изменения температуры dT/dt пропорциональна разности Т – Тс, то есть
dT/dt = - r(Т – Тс).
Минус означает, что с возрастанием времени t температура Т тела уменьшается. Производная убывающей функции отрицательна, а скорость по смыслу – положительная величина. Коэффициент пропорциональности r зависит от физических свойств тела, так и от его геометрической формы.
Разделим переменные в уравнении и проинтегрируем его:
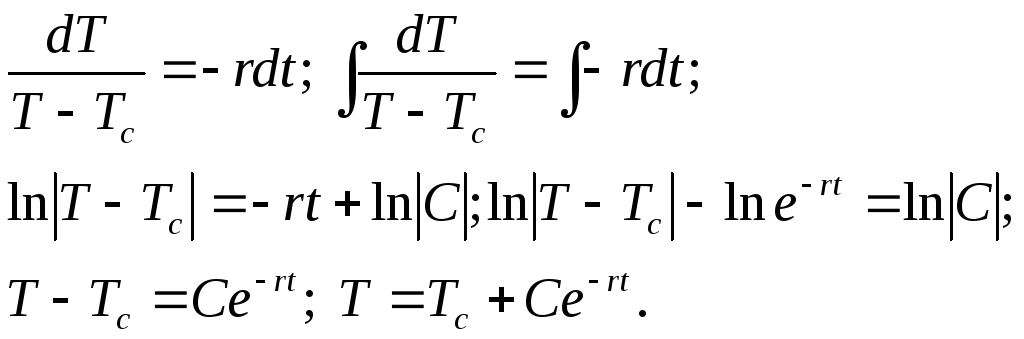
Подставив начальные условия t=0, Т=То, найдем значение С и подставим в последнее уравнение:
Т0=Тс+Се-r0; С=Т0-Тс;
Т=Тс+(Т0-Тс)е-rt.
Это закон охлаждения тела с течением времени.
