23. Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение. (часть2).

Распределение и характеристики непрерывной случай­ной величины. Непрерывную случайную величину нельзя за­дать тем же законом распределения, что и дискретную. В этом случае поступают следующим образом.

Пусть dP — вероятность того, что непрерывная случайная ве­личина X принимает значения между х и х + dx. Очевидно, что чем больше интервал dx, тем больше и вероятность dP: dP  dx. Кроме того, вероятность должна зависеть и от самой случайной величины, вблизи которой расположен интервал, поэтому

dP = f(x)dx, (2.15)

где f(x) — плотность вероятности, или функция распределе­ния вероятностей. Она показывает, как изменяется вероят­ность, отнесенная к интервалу dx случайной величины, в зависи­мости от значения самой этой величины:

f(x) = dP/dx.

Интегрируя выражение (2.15) в соответствующих пределах, находим вероятность того, что случайная величина принимает ка­кое-либо значение в интервале (ab):

(2.17)

Условие нормировки для непрерывной случайной величины имеет вид

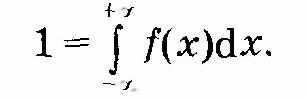(2.18)

Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной вели­чины:

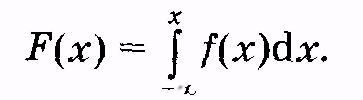(2.19)

Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:

Для непрерывной случайной величины математическое ожидание и дисперсия записываются соответственно в виде

(2.20)

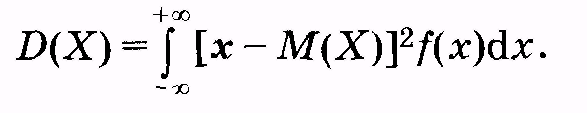
24.Примеры различных законов распределения. Нормальный закон распределения.(часть 1).

В теории вероятностей и математической статистике, в различ­ных приложениях важную роль играет портальный закон рас­пределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность вероятности ее имеет вид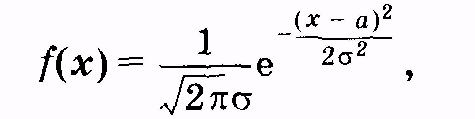

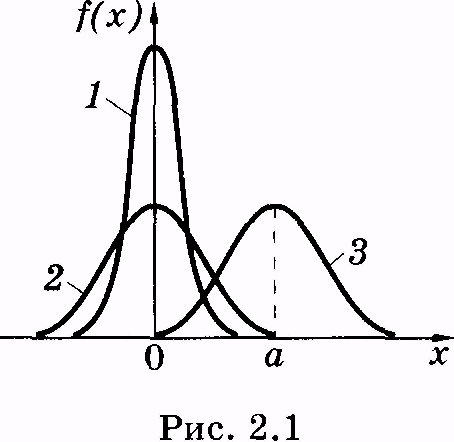
где а = М(Х) — математическое ожидание случайной величины; а — среднее квадратическое отклонение; следовательно, ² — дисперсия случайной величины.

Кривая нормального закона распределения имеет колоколообразную форму (рис. 2.1), симметричную относительно прямой х = а (центр рассеивания). В точке х = а функция достигает максимума:Для кривых1 и 2 а = 0, эти кривые отличаются зна­чением  (₁ < ₂); кривая 3 имеет а  0 ( = ₂).

Вычислим функцию распределения для этого случая:

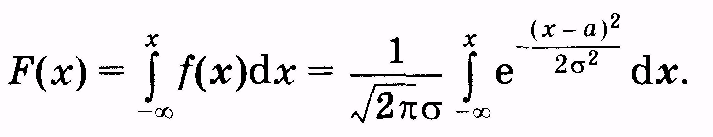
(2.23)

Обычно используют иное выражение функции нормальногораспределения. Введем новую переменную , следовательно, dx = dt. Подставив эти значения в (2,23), получим

(2.24)

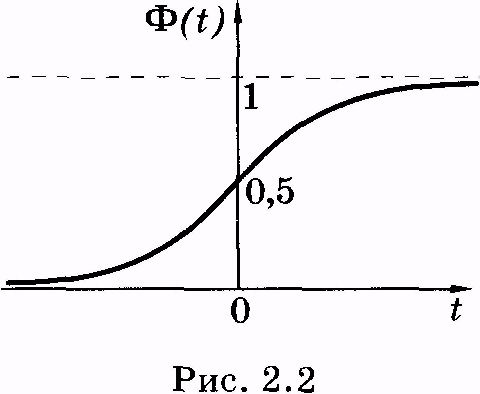
Значения функции Ф(t) обычно находят в специально состав­ленных таблицах так как интеграл (2.24) через элемен­тарные функции не выражается. График функции Ф(t) изображен на рисунке 2.2.

На основании можно вычислить вероятность того, что случайная величина при нормальном распределении находится в интервале (х₁, х₂). Без вывода, по аналогии с (2.24), укажем, что эта вероятность равна

(2.25)