30. Свободные затухающие колебания. Период колебаний.

Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. При достаточно большом сопротивлении контура колебания в нем вообще не возникают, а происходит апериодический разряд конденсатора.

Получаем дифференциальное уравнение затухающих колебаний: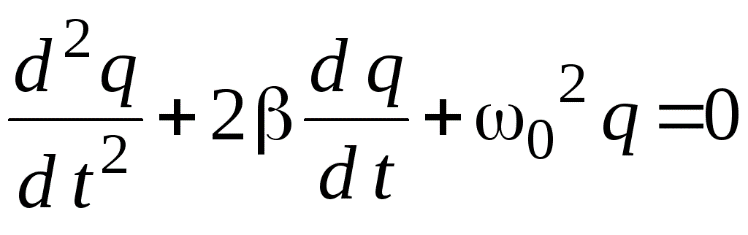

где β – коэффициент затухания.

При условии, что β² < ω₀², то есть <, решение уравнения имеет вид

где ω – частота затухающих колебаний, равная

.

Период колебаний в контуре определяется формулой Томсона:

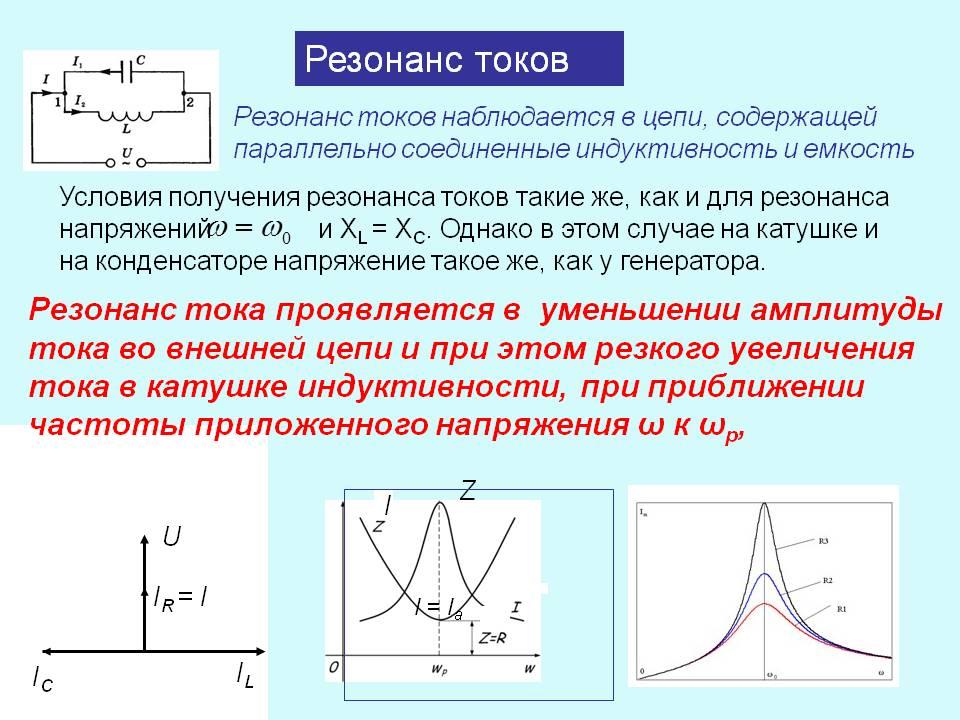
31. Вынужденные электрические колебания. Резонанс.

Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой , включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω₀.

Если частота ω₀ свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте  внешнего источника.

Для установления стационарных вынужденных колебаний необходимо некоторое время Δt после включения в цепь внешнего источника. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.

Электрические цепи, в которых происходят установившиеся вынуж­денные колебания под действием периодического источника тока, назы­ваются цепями переменного тока

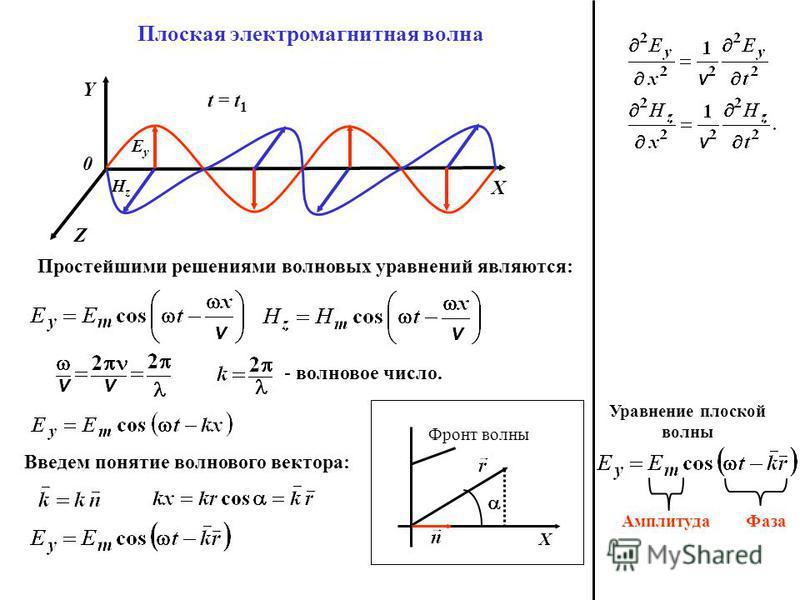
32. Возникновение электромагнитной волны. Волновое уравнение для электромагнитного поля. Плоская электромагнитная волна.

Существование электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью, следовало из уравнений Максвелла. В однородной и изотропной среде, не поглощающей энергию, вдали от зарядов и токов, создающих электромагнитное поле, векторы напряженностей и переменного электромагнитного поля удовлетворяют так называемому волновому уравнению:

Символ  означает дифференцирование по координатам.

Всякая функция, удовлетворяющая уравнениям, описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением

Где с- скорость электромагнитных волн в вакууме.

Электромагнитную волну называют плоской, если векторы и зависят только от времени и одной декартовой координаты.

Для плоской электромагнитной волны, распространяющейся вдоль положительного направления оси Ox правовинтовой системы координат, уравнения электромагнитной волны запишутся в следующем виде:

где n– единичный вектор, проведенный в направлении распространении волны. Мы видим, что плоская электромагнитная волна может быть полностью определена с помощью одного лишь векторного потенциала A.

В вакууме: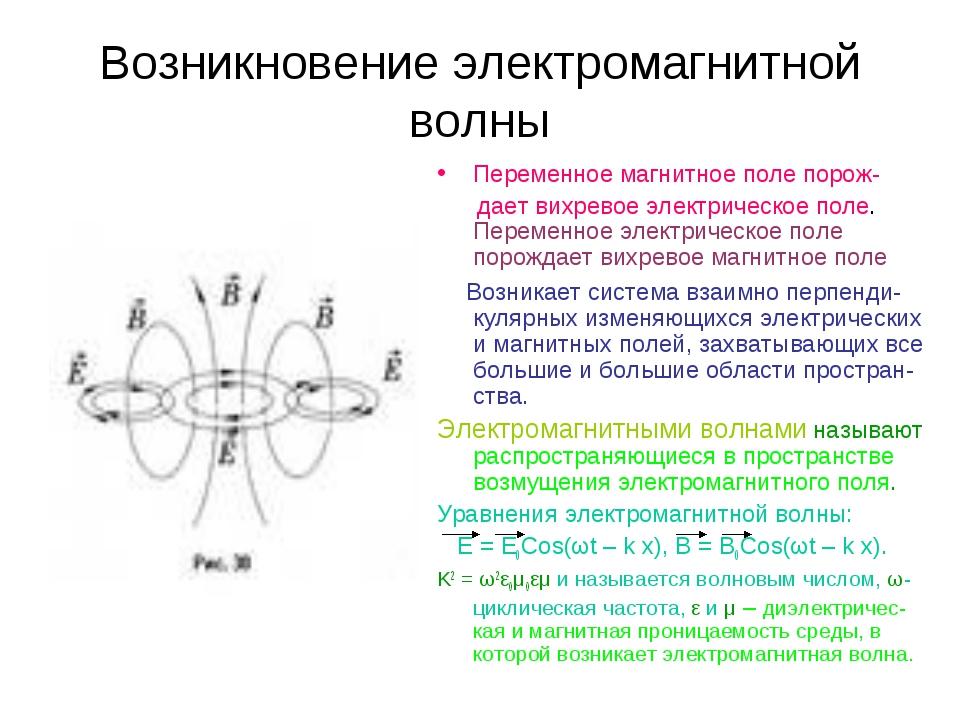

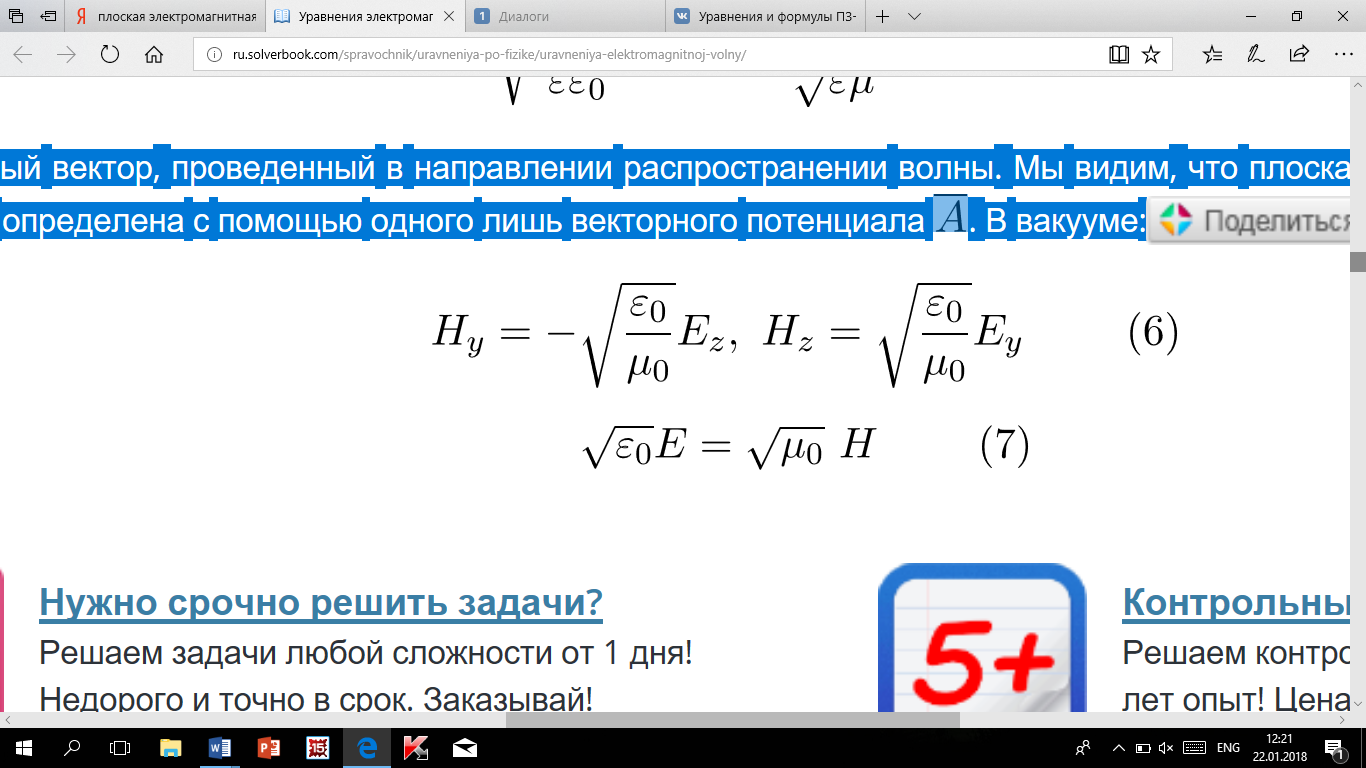
33. Плоская электромагнитная волна. Монохроматическая волна. Связь векторов В и Е.

Электромагнитную волну называют плоской, если векторы E и H зависят только от времени и одной декартовой координаты.

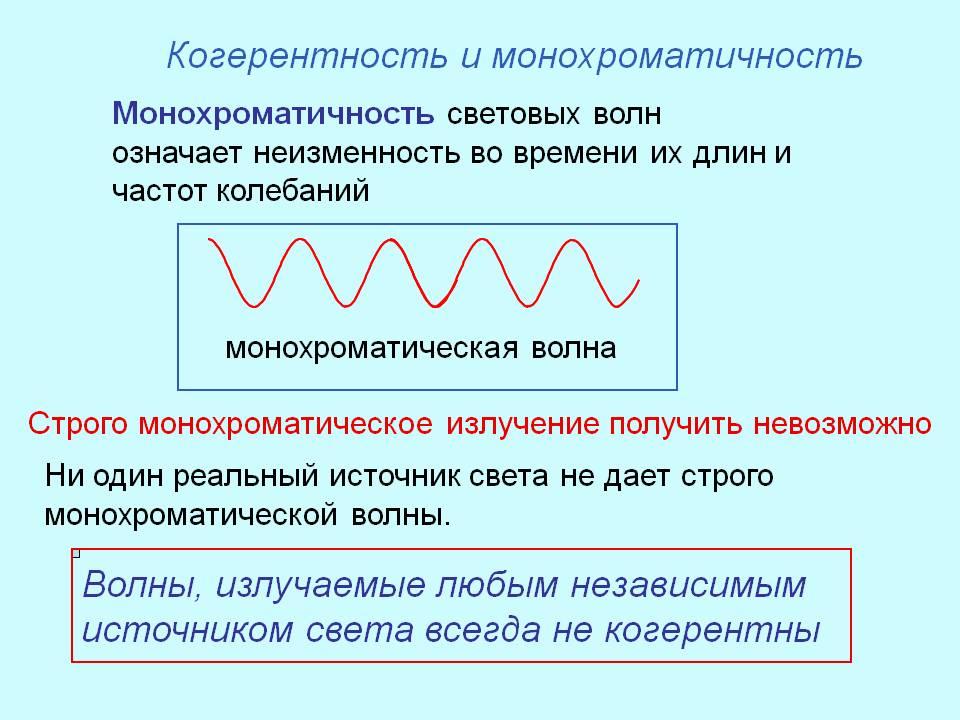
Электромагнитную волну называют монохроматической, если компоненты векторов E и H электромагнитного поля волны совершают гармонические колебания одинаковой частоты, называемой частотой волны.

Связь векторов B и Е

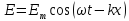
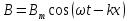
(где: 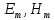- амплитуда,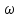-циклическая частота,k-волновое число).

В вакууме: B , ,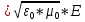

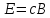
В веществе: 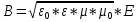, , 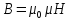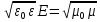H

34. Энергия электромагнитных волн. Вектор Пойнтинга.

35. Световая волна. Световой вектор. Интенсивность света.

Световая волна- электромагнитная волна видимого диапазона длин волн.

(где: А- амплитуда световой волны)

Частота световых волн очень велика, поэтому приемник света или глаз фиксирует усредненный по времени поток. Интенсивностью света называется модуль среднего по времени значения плотности энергии в данной точке пространства. Для световой волны, как и для любой электромагнитной волны, интенсивность равна: I=<EH>

36. Поляризация света. Получение и свойства поляризованного света.

Поляризацией света называется выделение из пучка естественного света лучей с определенной ориентацией электрического вектора.

37. Интерференция когерентных волн: интенсивность суммарной волны, условия максимума и минимума.

Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при определенных условиях при наложении двух или нескольких световых пучков.Интерференция волн – сложение в пространстве двух (или нескольких) волн, при котором в разных его точках получается усиление или ослабление результирующей волны. Для образования устойчивой интерференционной картины необходимы когерентные (согласованные) источники волн.Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз.Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.

Условия максимума и минимума