
- •Механика
- •1. Система отсчета. Радиус-вектор материальной точки. Закон движения материальной точки (мт).
- •2. Вектор перемещения (мт). Путь. Скорость. Ускорение.
- •3. Угловая скорость. Угловое ускорение.
- •4. Нормальное и тангенциальное ускорения.
- •5. Пространство и время в движущихся системах отсчета. Закон инерции Галилея. Инерциальные системы отсчета (исо). Преобразования Галилея и следствия из них.
- •Пример преобразования Галилея:
- •15. Уравнение Ньютона-Эйнштейна. 2-й закон Ньютона.
- •16. Момент силы. Момент импульса частицы. Момент инерции.
- •Электромагнетизм и электромагнитные волны
- •Фундаментальные свойства зарядов
- •2. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции.
- •3. Потенциал электрического поля. Эквипотенциали. Связь потенциала и напряженности электрического поля.
- •Где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей у и z, можем найти вектор ё:
- •4. Проводник в электрическом поле. Электростатическая индукция.
- •5. Атомы и молекулы в электрическом поле.
- •6. Поляризация диэлектриков. Вектор поляризации. Диэлектрическая проницаемость вещества. Электрическое смещение.
- •7. Сегнетоэлектрики. Пьезоэлектрический эффект. Обратный пьезоэлектрический эффект.
- •8. Электрическое поле заряженного проводника. Электроемкость проводника.
- •9. Конденсаторы. Поле внутри плоского конденсатора.
- •10. Энергия системы зарядов. Энергия электрического поля.
- •11. Классическая теория электропроводности. Закон Ома в дифференциальной (локальной) форме. Закон Ома для однородного проводника.
- •12. Закон Джоуля – Ленца в дифференциальной форме. Закон Джоуля-Ленца для однородного проводника.
- •18. Контур с током в магнитном поле.
- •19. Атомы и молекулы в магнитном поле. Парамагнетики.
- •20. Диамагнетики. Природа диамагнетизма.
- •21. Вектор намагниченности. Магнитная проницаемость вещества. Напряженность магнитного поля.
- •22. Ферромагнетики. Домены. Петля гистерезиса.
- •26. Явление самоиндукции. Индуктивность.
- •27. Энергия магнитного поля. Объемная плотность энергии.
- •28. Гипотеза Максвелла: магнитоэлектрическая индукция.
- •30. Свободные затухающие колебания. Период колебаний.
- •31. Вынужденные электрические колебания. Резонанс.
- •32. Возникновение электромагнитной волны. Волновое уравнение для электромагнитного поля. Плоская электромагнитная волна.
- •38. Методы получения когерентных источников (методы наблюдения интерференции).
- •Квантовая механика
- •1. Фотоэффект. Квантовый характер электромагнитного излучения. Формула Эйнштейна для фотоэффекта.
- •2. Фотоны. Энергия, масса и импульс фотона. Корпускулярно-волновой дуализм света.
- •3. Гипотеза де Бройля. Волна де Бройля. Экспериментальное подтверждение волновых свойств частиц.
- •А)Опыт к. Дэвиссона и л. Джермера (1927 г.)
- •B) Опыт Томсона и Тартаковского.
- •4. Особенности описания движения микрочастиц. Соотношения неопределенностей.
- •5. Уравнение Шрёдингера. Волновая функция.
- •6. Частица в одномерной бесконечно глубокой потенциальной яме.
- •7. Квантовый гармонический осциллятор. Энергия нулевых колебаний.
- •10. Уравнение Шредингера для атома водорода. Квантовые числа.
- •Основные квантовые числа
- •13. Строение многоэлектронного атома. Периодическая система элементов Менделеева.
- •Термодинамика и статистическая физика
- •1. Макросистема и методы ее описания. Контакты систем. Температура.
- •2. Тепловое равновесие. Уравнение состояния. Модель идеального газа.
- •3. Равновесные процессы. Изопроцессы.
- •6. Теплота. 1-е начало термодинамики.
- •7. Теплоемкость идеального газа. Соотношение Майера.
- •8. Зависимость теплоемкости многоатомного газа от температуры.
- •38. Лазеры. Процесс генерации.
- •39. Лазеры. Создание инверсной населенности.
- •40. Фермионы. Распределение Ферми-Дирака. Заполнение электронами разрешенных уровней в кристалле.
- •41. Энергетические уровни в атоме и энергетические зоны в кристалле.
- •42. Распределение электронов по квантовым состояниям в кристалле. Проводники и диэлектрики.
- •51. Деление ядер. Цепная реакция деления. Ядерные реакторы.
- •54. Квантовые числа элементарных частиц. Частицы и античастицы.
Механика
1. Система отсчета. Радиус-вектор материальной точки. Закон движения материальной точки (мт).
Система отсчета — это совокупность тела отсчета, связанной с ним системы координат и системы отсчета времени, по отношению к которой рассматривается движение каких-либо тел.
(Вот поставил на себе жирную белую точку мелом - всё, теперь считаешь себя точкой с координатами (0;0;0). А когда поставил точку - это считаешь, что пошло время (с 0 секунд и до бесконечности... плюс бесконечности - для особых умников). Всё, теперь ты - система отсчёта! Относительно тебя, например, крутятся Земля и другие планеты. Ну прямо центр Вселенной! Вкратце и поумнее: для положения тела необходимо определить систему отсчёта (это "отправная" точка с координатами (0;0;0) и начало отсчёта времени), относительно которой будет считаться всё, что связано с тем, как оно движется. Если относительно данной системы отсчёта тело меняет своё положение, то считаем, что оно двигается.)
Радиус-вектор — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.
Материальной точкой называется физическое тело, размерами которого можно пренебречь.
Закон движения мт: математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
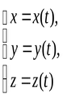 ,
а
при координатном способе он может быть
записан в виде
,
а
при координатном способе он может быть
записан в виде![]()
2. Вектор перемещения (мт). Путь. Скорость. Ускорение.
Перемещением
называется векторная физическая
величина, равная вектору, соединяющему
начальное положение материальной точки
с ее текущим положением. Перемещение
материальной точки равно разности
радиус-векторов этой точки, соответствующих
текущему ее положению и ее начальному
положению. (Тело
переместилось из точки А в точку Б. При
этом перемещение тела – отрезок,
соединяющий данные точки напрямую –
векторная величина.)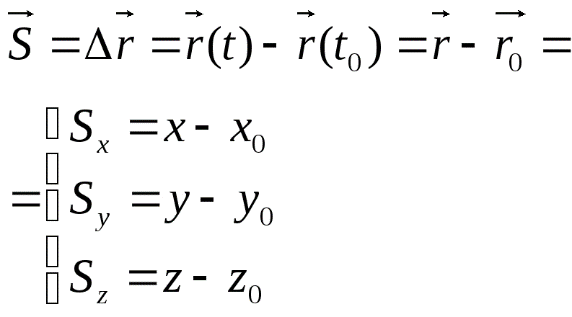
Траекторией данной точки тела называется множество точек пространства, проходимых этой точкой во время движения тела.
Для описания движения м. точки необходимо задавать кинематический закон движения, т.е. уравнение или систему уравнения, определяющих положение тела в любой момент времени относительно выбранной с. отсчета.
Путем называется скалярная физическая величина, равная длине траектории, пройденной телом за заданное время. ( Путь, пройденный телом – длина его траектории.)
Мгновенная скорость-скорость в данный момент времени. Мгновенная скорость тела, есть величина равная пределу отношению перемещения вектора r к промежутку времени t в течении которого это перемещение произошло при стремлении промежутка t к 0.
Средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь.
Ускорение характеризует быстроту изменения вектора скорости и определяется как производная скорости по времени:
Тангенциальное
ускорение
отвечает за изменение скорости по
величине: ![]()
Нормальное
ускорение
отвечает за изменение вектора скорости
по направлению:
![]()
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих.
Средним
ускорением называется
отношение изменения скорости к промежутку
времени, за который это изменении
произошло. Вычисляют среднее ускорение
при помощи формулы:
![]()
Мгновенное
ускорение тела
(материальной точки) в
данный момент времени – это физическая
величина, которая равна пределу, к
которому стремится среднее ускорение
при стремлении промежутка времени к 0.
Другими словами – это ускорение,
развиваемое телом за очень маленький
отрезок времени:
![]()
