6. Частица в одномерной бесконечно глубокой потенциальной яме.

Рассмотрим поведение частицы в бесконечно глубокой одномерной прямоугольной потенциальной яме.

Предположим, что частица движется вдоль оси Движение частицы ограничено областью 0 ≤ ≤ , в которой потенциальная энергия частицы (потенциальная энергия отсчитывается от дна ямы). За пределами ямы при < 0 и > потенциальная энергия В пределах ямы частица движется свободно. Сталкиваясь со стенками ямы, она отражается от них и изменяет направление своего движения. За пределы потенциальной ямы частица выйти не может. Волновую функцию, зависящую только от одной координаты обозначим Тогда уравнение Шредингера (7.44.10) примет вид:

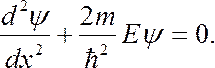(7.44.15)

За пределы ямы частица выйти не может, поэтому вероятность обнаружить ее, а следовательно и волновая функция , за пределами ямы равна нулю. Из условия непрерывности следует, что и на границах ямы должна быть равна нулю, т.е.:

(7.44.16)

Этим граничным условиям должны удовлетворять решения уравнения (7.44.15). Обозначим Тогда уравнение (7.44.15) примет вид:

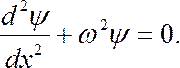(7.44.17)

Решение уравнения (7.44.17) имеет вид:

(7.44.18)

Значения и найдем, используя граничные условия (7.44.16). Из условия получим:

откуда следует, что Выполнение условия

возможно в том случае, если

. (7.44.19)

Откуда

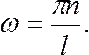(7.44.20)

Из (7.44.19) следует, что решения уравнения будут иметь физический смысл лишь при значениях энергии, удовлетворяющих соотношению:

( 1, 2, 3, …).

Отсюда найдем собственные значения энергии:

( 1, 2, 3, … ) (7.44.21)

Условие квантования энергии получено непосредственно из решения уравнения Шредингера без дополнительных предположений. Подставив (7.44.20) в (7.44.18), получим собственные функции для данной задачи:

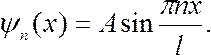(7.44.22)

Коэффициент найдем из условия нормирования волновой функции:

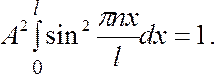(7.44.23)

Откуда

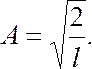(7.44.24)

С учетом (7.44.24) собственные функции принимают вид:

( 1, 2, 3, …). (7.44.25)

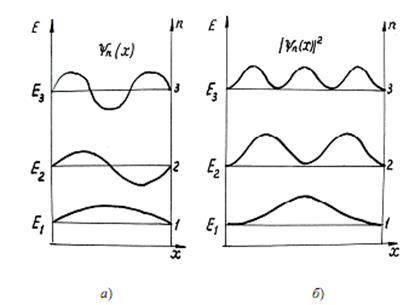
Графики функций изображены на рисунке для различных значений

7. Квантовый гармонический осциллятор. Энергия нулевых колебаний.

Классическим осциллятором в классической механике называли частицу массой m, колеблющуюся с частотой w₀=Ök/m под действием упругой силы F=-kx.

Потенциальная энергия такой частицы U=kx²/2=mx²/2; в точках с координатами ±х_max она равна полной энергии Е. Т.о., энергия частицы могла принимать любые значения, т.е. изменяться непрерывно (рис.6).

В квантовой механике понятие силы не используется, поэтому квантовый осциллятор следует определить как частицу с потенциальной энергией U=kx²/2=mx²/2. (34)

Подставляя (34) в (22) и учитывая, что частица движется только вдоль одной прямой (вдоль оси х), получим

. (35)

Решая уравнение (35), можно получить, что энергия (энергетический уровень) частицы принимает только дискретные значения (квантуется).

(36)

n=0, 1, 2... – квантовые числа.

Наименьшее значение энергии E₀=w₀/2 определяется только собственной частотой w₀ и ее невозможно отнять у частицы никаким охлаждением, она сохранилась бы и при Т=0К.

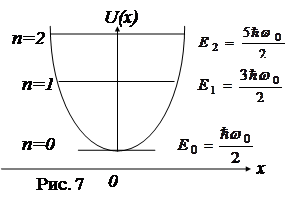Из (36) следует, что уровни находятся на равных расстояниях друг от друга

(37)

т.е. уровни эквидистантны [см. рис. 7, где на границе с потенциальной кривой U(±х_max)=Е_n]. При больших квантовых числах n DЕ/Е_n=1/(n+1/2)®0, т.е. происходит относительное сближение энергетических уровней и получаются результаты, близкие к результатам классического рассмотрения, когда энергия частицы может изменяться непрерывно, и, следовательно, может иметь любые значения. В этом заключается принцип соответствия, сформулированный Бором в 1923 г.:

При больших квантовых числах выводы и результаты квантовой механики должны соответствовать выводам и результатам классической механики.

Более общая трактовка принципа соответствия заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения. Причем в определенных, предельных случаях, новая теория переходит в старую.

8. Спектр излучения атома водорода. Постулаты Бора.

Постулаты Бора: 1)Существует стационарные орбиты электрона, при движении по которым излучения энергии не происходит. E=E_n n=1, 2, 3…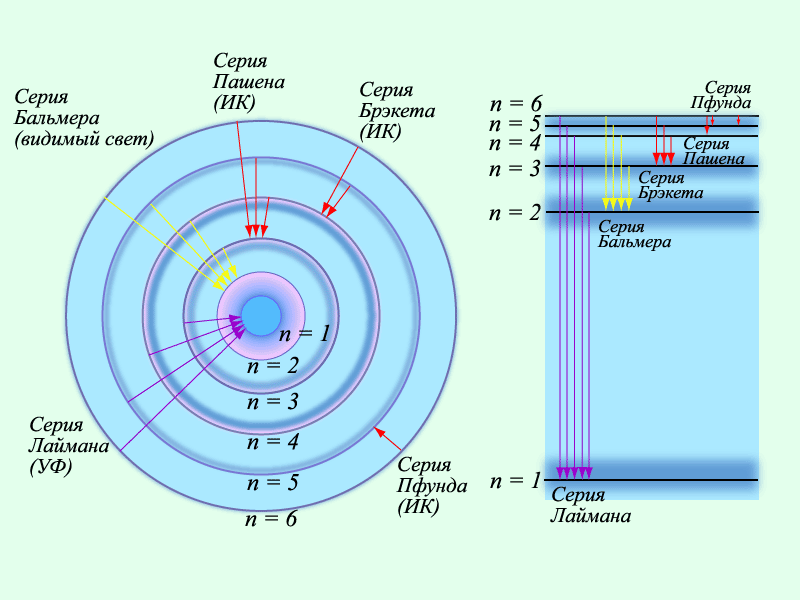

2)При переходе электрона с орбиты на орбиту поглощается или испускается фотон.

E_n-E_m=hν, ν-частота

3)Орбитальный момент импульса электрона квантуется. L=mvr = nh

9. Боровская теория атома водорода. Квантование энергии электрона.

Боровская теория атома водорода позволяет объяснить происхождение линейчатых спектров испускания, связывая их появление с наличием дискретного ряда энергетических состояний атомов и переходами между ними. Согласно представлениям Бора, движение электронов вокруг ядра в стационарных состояниях определяется законами обыч­ной механики, для описания же процессов перехода атома из одного стационарного состояния в другое эти законы не примени­мы, и следует воспользоваться квантовыми представлениями.

Первая квантовая теория строения атома была предложена Н. Бором. Он считал, что в изолированном атоме электроны двигаются по круговым стационарным орбитам, находясь на которых, они не излучают и не поглощают энергию. Каждой такой орбите отвечает дискретное значение энергии. Переход электрона из одного стационарного состояния в другое сопровождается излучением кванта электромагнитного излучения, частота которого равна: ν = ΔE / h, (где ΔE - разность энергий начального и конечного состояний электрона, h - постоянная Планка). Прерывистость энергии электрона является важнейшим принципом квантовой механики. Электроны в атоме могут иметь лишь строго определенные значения энергии. Им разрешен переход с одного уровня энергии на другой, а промежуточные состояния запрещены.