Юзвишин И.И. - Основы информациологии - 2000

сi периферийных терминалов, матрица которой представлена выражением (17.119). Если считать, что каждая задача а пользователей может быть решена одним из Zα способов, заключающихся в использовании соответствующего количества β модулей xij матрицы (17.119) МИСМО, то время решения этой задачи обозначим через tγ αβ (γ - способ решения задачи α). Зададим сроки решения задачи α из множества задач Ai терминала: время начала решения - Тнαp и время конца

431

решения - ТKαp. За начало работы МИСМО примем момент времени H0=0, а момент времени, когда освобождается i-й терминал от решения задачи α, обозначим через tα. Время эксплуатации МИСМО примем в пределах 0 ≤ tэ≤Тνэ. При H0=0 все моменты t'j для С терминалов тоже будут равны нулю, т.е. t1=t2=t3=...=tc=0.

Приняв приведенные обозначения, приступим к синтезу алгоритма модели эффективного функционирования МИСМО для структурной модели (17.106), блок-схема которого представлена на рис. 17.3.

1. Исходные данные: H0=0;tj= С=1, где С- число терминалов. В момент H1=0, t0=0 на одном из С терминалов работает один пользователь. Общее количество просчетов алгоритма с целью оптимальных параметров МИСМО равно N, следовательно, первый просчет и их группу запишем как

1 N1≤N.

2.tj <Тνэ, j,ν = 1,n.Это означает, что терминалами можно пользоваться только в момент времени tj

<Тνэ;.

3.Если A>0, следует перейти к блоку, формирующему портфель задач (А - число задач, поступающих в портфель заказов).

4.Если i<C, т.е. номер i занятого терминала должен ,быть меньше максимального значения С номера эксплуатируемого терминала, то в счетчик числа занятых терминалов записывается единица i:=i+1. Если условие i<C не соблюдается, то переходим к блоку свободных терминалов Ссв>0.

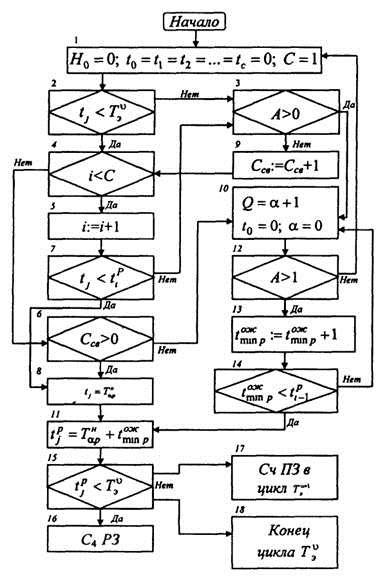
Рис 17. 3 Блок-схема алгоритма ИСМО

5.i:=i+1 - счетчик числа занятых терминалов.

6.Если Ссв>0, переходим к формированию момента ТНαp начала решения задачи на одном из Ссв свободных терминалов.

7.Если tj момент времени поступления j-й задачи меньше момента времени решения предыдущей (j- 1)-й задачи на i-м терминале, переходим к блоку 8. Если условие tj <tpi не соблюдается, переходим к блоку 3.

432

8.Формирование момента ТНαp начала решения α-й задачи.

9.Если условие А>0 не соблюдается, переходим к блоку 9, реализующему операции счетчика свободных терминалов.

10.Формирование портфеля заказов Q=α+1. В момент времени t0=0, α=0, а при t1>0 и А>0,α>0 и, следовательно, Q= α+1≥2.

11.Определение общего времени пребывания задачи в МИСМО, равному сумме времени начала решения и времени ожидания по критерию минимального времени решения tpj = Тнαp + Тожmin p.

12.Если число задач в очереди А>1, то из них выбирается тот номер задачи, время решения которой наименьшее. Если условие А>1 не соблюдается, управление передается на блок 1.

13.tожmin p:=tожmin p+1.

14.Если tожmin p < tpi+1, т.е., если минимальное время решения задачи, ожидающей в очереди, меньше времени решения задачи на (i-1)-м терминале, переходим к блоку 11. Если условие не

выполняется, из блока 10 выбираем новое значение t''cmin p, удовлетворяющее условию и, таким образом, критерию минимального времени решения задачи.

15.Если tpj < tvэ , переходим к блоку 16, реализующему счетчик решенных задач. Если условие не соблюдается, переходим к блоку 17, реализующему счетчик переходящих задач во второй цикл расчета Tv+1э.

Таким образом, рассмотрен алгоритм модели решения задач многотерминальной ИСМО, с помощью которого можно осуществить несколько просчетов и по полученным результатам отдельных параметров во всех просчетах найти их математические ожидания, которые и будут являться основой определения оптимальных значений этих параметров для данного алгоритма функционирования МИСМО.

433

430 :: 431 :: 432 :: 433 :: Содержание 433 :: 434 :: 435 :: 436 :: 437 :: 438 :: 439 :: 440 :: Содержание

17.9. Методика исследования системы в переходном режиме

С целью изучения работы ИСМО и определения вероятностных характеристик, позволяющих оценивать ее состояния в любой момент времени, разработана методика решения системы дифференциальных уравнений, описывающей поведение ИСМО в переходных режимах, которая в общем виде может быть записана следующим образом:

Xi=

n

∑

j=1

aijx j, i,j =1,n(17,123)

Систему дифференциальных уравнений (17.123) запишем в векторной форме:

Х=АХ, (17.124)

433

где X =

dPi

dt

- вероятность того, что ИСМО в момент времени Δt находится в i-м состоянии; А - матрица коэффициентов при неизвестных вероятностях состояний системы; коэффициенты представляют собой значения потоков (λ, μ), переводящих систему из одного состояния в другое.

Согласно теореме Понтрягина о решении однородной системы дифференциальных уравнений частные решения уравнения (17.124) можно представить в следующем виде:

x1=h1e S1t,...;

x m1=(

tm1-1

(m1-1)!

h1+...+h m1)eS1t;

xm1+1 =h m1+1 e S2t ,...,x m1+m2 = (17.125) =(

tm2-1

(m2-1)!

m1+1 +...+ h m1+m2 )eS2t ,

...................................

где S1, S2, S3, ..., Sn - корни характеристического уравнения |A-SE|=0 (A - матрица коэффициентов; Е - единичная матрица); m1 m2, m3... - кратности соответствующих корней характеристического многочлена; h1,..., h m1 - собственные векторы матрицы A.

Общим решением системы уравнений (17.124) является линейная комбинация всех частных решений (17.125), т.е.

х = C11 + С2х2 +C3x3 + + Cnx n,(17.126)

где С1, С2,..., Сn - произвольные постоянные (константы).

Используя матричный анализ, определим корни характеристического многочлена |A-SE|для семи состояний ИСМО:

S12 = -λ; S34= -2λ; S67 = λ(-3 ± √2i) (17.127)

Анализ характеристического многочлена и значений пяти характеристических корней позволил определить их кратности: кратность первого корня S 12-m1 = 2; кратность второго S 34-m2= 2 третьего S 5-m3=1 ; четвертого S 6-m4 = 1 ; пятого S 7-m5 = 1

Дальнейшее исследование математической модели ИСМО в переходном режиме заключается в определении: серии собственных векторов h матрицы А;частных решений приведенной к векторной форме (17.124) системы дифуравнений состояний ИСМО; серии произвольных постоянных СI частных решений. Поставленные задачи решены на основании использования матричного анализа и теории обыкновенных дифференциальных уравнений. Каждому собственному значению

характеристического корня согласно установленным кратностям получены собственные значения следующих векторов матрицы А:

434

h1={0,0,0;0,-(b6+b7),b6,b7}; h2={0,0,0,0,-(a6+a7),a6,a7}; h3={0,0,0,0,-(α6+α),-(α6+α7),α6α7}; h4={0,β7,β6,-(β6+β7),-(β6+β7 ),β6 ,β7}; h5={l1;0,5l1;0,5l1;0,5l1;l1,l1,l1};

h6={n1,n1(- 1

3

-

√2

3

i), n1(- 1

3

-

√2

3

i), (17.128)

n1(- 1

3

-

√2

3

),n1

√2

3

i, n1

√2

3

i, n1

√2

3 i};

t m1-1

(m1-1)!

h1+h m1)e S12t=

=h1te -λt+h2e -λt={0,0,0,0,-a6e -λt,0};

x4=x m1+m2=( tm2-1

(m2-1)!

h m1++h m1+m2)e S34t=

(

t2-1

(2-1)!

h 2+1+h 2+2)e S34t=h3te -2λ+h4e -2λt=

={0,β7e -2λt ,β6e -2λt ,-(β6+β7)e -2λ ,- -(β6+β)e -2λt ,α6e -2λt ,α7e -2λt }.

435

Используя формулу Эйлера комплексной переменной, найдем шестое и седьмое решения:

x6=h 6e S6t =h6eλ(-3+√2i)t=

=h6e -3λ+λt√2i=h6e -3λt∙(cos√2λt+isin√2λt);

(17.131)

x7=h7 e S7t =h7e λ(-3-√2i)t = =h7e -3λt∙(cos√2λt-isin√2λt).

Умножим числовые значения n1 векторов h6 и h7 на формулу Эйлера соответственно комплексными числами, равными четвертому корню S6 = λ(-3 + √2i) и пятому корню S7= λ(-3 - √2i)

для h6:

1)(-

1

3 - (17.132)

√2

3

i)e λ(-3+√2i)t=e -3λt(-