Юзвишин И.И. - Основы информациологии - 2000
.pdf
on - line при n = 2,3,4,..., G|G|m|n{ off-line при n=0 (17.9)
399
1 Феллер В. Введение в теорию вероятностей и ее приложения. М., 1964. Т.1.
386 :: 387 :: 388 :: 389 :: 390 :: 391 :: 392 :: 393 :: 394 :: 395 :: 396 :: 397 :: 398 :: 399 ::
Содержание
399 :: 400 :: 401 :: 402 :: 403 :: 404 :: 405 :: 406 :: Содержание
17.2. Теорема о генерализационном потоке информации
При проектировании локальных многотерминальных информационно-справочных систем массового обслуживания, информационно-биологических или информационно-космических систем необходимо знать, каким генерализационным (обобщенным) законом можно аппроксимировать распределение очень большого числа входящих потоков информации при заданной суммарной их интенсивности. На этот вопрос можно ответить, доказав следующую теорему.
Теорема. Если имеется бесконечное (счетное) число однородных независимых потоков информации (не разнесенных во времени), каждый из которых описывается не обязательно одинаковым законом распределения и соответствующей интенсивностью λi (t), то при совмещении начальных моментов t0 возникновения источников потоков информации на некоторой регламентированной по времени вещественной оси 0t распределение генерализационного потока информации с интенсивностью λ =
n
∑
i=1
λi (t) будет близкое к пуассоновскому.
Доказательство. Обозначим через Δt1i случайную величину, заданную законом распределения:
399
Δt11Δt12Δt13 ... Δt1n p11 p12 p13 ... p1n
(17.10)
Обозначим через Δt2i случайную величину, значение которой тоже заданы указанным законом распределения. Запишем законы распределения вероятностей для других аналогичных случайных величин:
Δt21 Δt22 Δt32 ... Δt2n p21 p22 p32 ... p2n
Δt31 Δt32 Δt33 ... t3n p31 p32 p33 ... p3n
........................
Δtm1 Δtm2 Δtm3 ... Δtmn pm1 pm2 pm3 ... pmn
(17.11)
Заметим, что для законов распределения (17.10) и (17.11) приняты следующие ограничения:
Δtji < Δtj+αi+k при: i = 1,n; j = 1,m; k =1,n-1;α = 1,m-1.
Запишем случайные величины моментов возникновения источников информации и их вероятности в виде матрицы случайных величин и матрицы вероятностей:
|
t1 |
t2 |
t3 |
... tn |
|
П1 |
Δt11 |
Δt21 |
Δt31 |
... Δtn1 |
λ1 |
П2 |
Δt21 |
Δt22 |
Δt32 |
... Δtn2 |
λ2 |
П3 |
Δt31 |
Δt32 |
Δt33 |
... Δtn3 |
λ3 |
... |
... ... ... ... ... |
... |
|
T = Пm(Δtm1Δtm2Δtm3 ... Δtmn)λm |
|||
|
Δp11 Δp21 Δp31 |
... Δpn1 |
|
|
Δp21 Δp22 Δp32 |
... Δpn2 |
|
|
Δp31 Δp32 Δp33 |
... Δpn3 |
|
|
... ... ... ... ... |
|
|
P = (Δpm1Δpm2Δpm3 |
... Δpmn) |
|
|
Из матрицы (17.12) для каждого из потоков Пi определим математическое ожидание:
400
n M i=1
(Δt11)=a1n
n M i=1
(Δt21)=a2n
................
n M
i=1
( tmi)=amn
(17.14)
А так как математическое ожидание суммы нескольких случайных величин равно сумме слагаемых, то получим:
an=
n,m
∑
i,j=1
aji. (17.15)
Следует отметить, что в матрице (17.13)
p=
n,m
∑
i,j=1
pji=1.
Аналогично определим среднее квадратичное отклонение случайной величины:
σ2(Δt1i)=(σ1n)2 σ2(Δt2i)=(σ2 n)2 σ2(Δtmi)=(σmn)2.
(17.16)
Запишем сумму квадратов средних квадратических отклонений
σ2 n=
n,m
∑
i,j=1
(σj i)2 или σn=√
n,m
∑
i,j
(σj i)2.(17.17)
Конечное число взаимно независимых случайных величин также представим в виде суммы
tn=
n,m
∑
i,j
Δtji. (17.18)
Интенсивность генерализационного суммарного потока информации, очевидно, равна сумме интенсивностей конечного числа частных потоков
λ=
m
∑
i=1
λi(t). (17.19)
401
Рассмотрим в качестве новой случайной величины разность между суммарной случайной величиной tn и ее суммарным математическим ожиданием аn,называемой отклонением или центрированной случайной величиной
K° n=tn-an. (17.20)
Разделив центрированную величину на суммарное значение среднего квадратичного отклонения и записав функцию распределения новой суммарной величины, получим,
Pn =(T<t) = Pn [(tn-an)/<t]=Pn (K° n <tσn).(17.21)
Преобразуем выражение под знаков вероятности следующим образом
(-t <
K° n
σn
) < t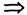 
(-σnt <K° n < σnt (17.22)
Ввиду того, что суммарная случайная величина может принять значение, принадлежащее интервалу (- σn t,σnt), функция распределения вероятностей (17.21), переписанная с учетом (17.22), будет равна определенному интегралу от плотности распределения суммарной случайной величины К° n с пределами интегрирования от - σn t до σnt :
Pn(-σn t < K° n<σnt=
σnt
∫
-σnt
f(K° n) dK° n (17.23)
Пусть суммарная случайная величина К° n распределена по нормальному закону с плотностью распределения
f(K° n) =
1
σn(2π)1/2
e-(tn-an)2/2σ2n. (17.24)
Тогда, заменяя в (17.23) f(K° n) на выражение (17.24), получим вероятность того, что случайная величина К° n попадает в интервал (-σnt,σnt):
Pn(-σn t <K° n<σn t ) =
1
σn√2π
σnt
∫
-σn t
e -(tn-an)2/2σ2 n K° n (17.25)
402
Произведем некоторые преобразования. Пусть λ = (tn -аn)/σ , тогда tn = λσn +an и dtn ≈d K° n = σndσ. Найдем новые пределы интегрирования. Положим tn= –tσn, тогда λ = (-tσn, -аn)/σn = = -
(tσn, + an)/σn и tn = tσn , следовательно, λ = (tσn - an)/σn.
Перепишем функцию общего (суммарного) нормального распределения случайной величины с учетом преобразований
Pn=(-σnt <K° n< σnt) =
1
σn√2π
(tσn-an)/σn
∫
-(tσ +a )/σ n n n
e -λ2/2σndλ. (17.26)
Заменим f(K° n) асимптотически ей приближенной функцией φ(K° n) согласно предельному отношению
lim n→∞
=
f(K° n)
φ(K° n)
= 1 , φ(K° n), т.е. φ(K° n) =f(Kn) при n→∞ . Поскольку асимптотическая функция φ(K° n) при an = 0 и σm =1 является еще и нормированной, то (17.26) можно записать в следующем виде:
Рn = (-t <K° n<t} =
1
√2π t
∫
-t
е-λ2/2dλ.(17.27)
Следовательно, функция распределения центрированной случайной величины (суммарного потока) при п-→∞ стремится к функции нормального распределения.
Можно показать, что кривая нормального распределения (17.27) приближается к пуассоновскому распределению, производя расчеты двумя способами. Необходимо извлечь неопределенный интеграл правой части выражения (17.27). В результате чего получим асимптотическую функцию. Предварительно в (17.27) сделаем замену: – λ2/2 = z и продифференцируем обе части равенства: d(-λ2/2)= dz = (dλ2/2) = -dλ. Вычислим неопределенный интеграл путем извлечения дифференциала из функции распределения:
1
√2π
∫
е-λ2/2dλ =
1
√2π
∫
(-1)еzdz =
-
1
√2π
еz = -
1
√2π
е-λ2/2 = P1n(K° n) = φ(K° n)
Так как плотность нормированного распределения является четной и табулированной функцией, то
403
φ(K° n) =
1
√2π
е-λ2/2.
(17.29)
1
√2π
∞
∫
-∞
е-λ2/2dλ =
1
√2π
∞
∫
-∞
(-1)еzdz =
=
1
√2π
0
∫
-∞
(-1)еzdz +
1
√2π
∞
∫
-∞
(-1)еzdz
(17.30)
Поменяем, пределы интегрирования на реальные вещественные числа пределов распределения числовой оси
lim a→-∞
-
1
√2π
0
∫
a ezdz +
lim b→∞
-
1
√2π b
∫
0 ezdz =
=- 1
√2π
e-λ2/2
0
I
a
-
1
√2π
e-λ2/2
b
I
0
=
=
1
√2π
e-a2/2 -
1
√2π
e-b2/2 =
=
1
√2π
e-λ2t1/2 -
1
√2π
e-λ2t2/2 =
=
1
√2π eλ2t1/2
-
1
√2π eλ2t2/2
=
=
1
√2π e-λ2t1/2-0(Δ)≈
1
√2π
e-λ2t/2=φ(K° n).
(17.31)
Плотность распределения (17.29, 17.30) суммарной центрированной случайной величины имеет нормированную кривую, являющуюся асимптотическим приближением плотности нормального распределения.
Определим теперь плотность суммарной случайной величины входного потока информации, распределенную по закону Пуассона. Запишем функцию пуассоновского распределения через плотность распределения
F(k) = P(K <k)=
∞
∫
0
f(k)dk.(17.32)
Найдем по функции распределения ее плотность, взяв от нее производную
404
f(k) =
d
dk
P t (K<k). (17.33)
Если считать, что суммарная интенсивность в основном является постоянной, то вероятность появления E входящих потоков информации за интервал длительностью t является функцией распределения и зависит от К и t. Так как функция е -λ не зависит от К и от t, а только от λ=const, то ее можно вынести за знак производной. В результате дифференцирования выражения (17.32) получим аналитическую модель закона Пуассона:
d
dk
Pt(K<k) =
d
dk
(λt)k
k!
e -λt =
k(λt)k-1
k!
e-λt. (17.34)
Нормальный и пуассоновский законы, а также закон Эрланга аппроксимируются на положительной вещественной оси распределением Пуассона (при λ≥10), нормальным распределением (при λ = λ , σ = √λ, ) и параметрами Эрланга λ и k → ∞ , если число входящих потоков Пвх=4÷5≤П∑≤∞. С учетом указанных ограничений можно записать аппроксимированные тождества для следующих законов:
а) нормальный и пуассоновский
1
√2π
e-(λt)2/2 ≈
(λt)k-1
(k-1)!