
Юзвишин И.И. - Основы информациологии - 2000
.pdfn
∑
i=1
P ij = 1, т.е. сумма переходов вероятностей каждой строки матрицы перехода всегда равна единице.
Сделав соответствующие преобразования выражений (17.65) и (17.66), получим матрицу перехода стационарной системы за Z шагов:
M(Z) = [M(1)] z.(17.67)
Пример. Задана матрица перехода системы за один шаг
P11(1) P12(1) |
)= ( |
0,5 0,5 |
). |
M(2) = ( P21(1) P22(1)= |
0,6 0,4 |
Требуется определить матрицу перехода ИСМО из i-го в j-е состояние за три шага (Z=3).
Запишем матрицу перехода за три шага в соответствии с выражением (17.67):
( 0,545 0,455 ) M(3)=[M(1)]3= 0,546 0,454 .
Определим вероятности перехода системы за три шага: из 1-го в 1-е состояние Р11=(3)=0,545; из 1-
го во 2-е состояние P12 (3)=0,455; из 2-го в 1-е состояние P21 (3)=0,546; из 2-го во 2-е состояние P22
(3)=0,454.
С учетом того, что
n
∑
j=1
P ij= 1, проверим правильность вычислений:
2
∑
j=1
P 1j =
2
∑
j=1
P 2j=0,545+0,455=0,546+0,454=1. Следовательно, вероятность и матрица перехода определены верно.
Таким образом, изложенный метод анализа ИСМО с использованием цепей Маркова позволяет определять вероятности ее переходов из одних состояний в другие (за конечное число шагов), зная которые можно рассчитывать другие характеристики эффективности и качества функционирования ИСМО.
413
410 :: 411 :: 412 :: 413 :: Содержание 413 :: 414 :: 415 :: 416 :: 417 :: 418 :: 419 :: 420 :: Содержание
17.5. Методика расчета однотерминальной ИСМО
Рассмотрим однокомпьютерную или многокомпьютерную (одноили многопроцессорную) информационную систему, решающую задачи или отвечающую на вопросы многих пользователей в режиме непосредственного доступа, пакетном режиме, в режиме разделения времени или в реальном масштабе времени. Выделим из указанных ИСМО однотерминальные и многотерминальные системы.
413
Однотерминальной ИСМО назовем одноили многокомпьютерную систему, работающую в одном из указанных выше режимов, состоящую из одного или нескольких скомплексированных или нескомплексированных ПК, одного терминала, связанного с ЦЯ системы только по удаленному или только по локальному каналу связи. Многотерминальная ИСМО - это однокомпьютерная, многопроцессорная или многокомпьютерная система, соединенная через мультиплексоры передачи данных, каналообразующую аппаратуру, каналы связи и удаленные терминалы со многими пользователями и работающая в режиме разделения времени или в реальном масштабе времени.
В связи с тем, что однотерминальные и многотерминальные ИСМО - это системы настоящего и будущего Интернет, дадим методику расчета именно этих систем. В соответствии с классификацией, приведенной в табл. 3.1, рассчитаем основные вероятностные характеристики ИСМО класса:
on - line при п = 1, 2, ... |
}. (17.68) |
P|M|m|n={ off-line при и =0 |
В соответствии с условием (17.68) на вход такой системы поступает пуассоновский поток информации с плотностью λ, а на ее выходе имеется экспоненциальное распределение времени обслуживания с плотностью μ. Система может состоять из одного или нескольких ПК; она работает по принципу off-line при =0, т.е. локальные терминал и канал связи (ЛТКС) или по принципу on-line, при п=1. Обработка вводов (вопросов) является многофазовой.
Примем следующее символьно-логическое обозначение состояний ИСМО с целью облегчения исследований и расчета ее основных вероятностных характеристик.
Пусть С0 - ИСМО исправна и свободна (не загружена), т.е. ни по одной задаче информация не введена в систему; С1 - ИСМО загружена, решается (обрабатывается один вопрос) одна задача; С2 - ИСМО загружена, информация одной задачи подготовлена и сформирована для запуска на решение; С3 - ИСМО загружена, информация двух задач подготовлена и сформирована для запуска на решение и т. д.; Сn - ИСМО загружена, информация (n-1) задач подготовлена и сформирована для запуска на решение.
Схема размеченного графа указанных состояний однотерминальной ИВСМО приведена на рис. 17.1. Каждому состоянию поставим в соответствие вероятность того, что система будет в данный (фиксированный) момент времени именно в указанном состоянии, т. е.
C0 (t)→P0 (t),
C1 (t)→ P1 (t);...; Cn(t)→Pn (t). (17.69)
Переход из состояния Сi в Сj (i≤j) вызывается входным потоком информации с интенсивностью λij,
С0→ C1→λ01
C1→C2→λ12;...;Cn-1→Cn→λn-1,n.
(17.70)
414
Соответственно, переход ИСМО из состояния Сi в Сj (i>j) происходит с интенсивностью μij моментов времени завершения (обслуживания) решения задач:
C1→C0→μ10;
С2→С1 μ21;...; Сn →Cn-1 →μn,n-1.
(17.71)
Предположим, что в определенный момент времени t0 в ИСМО находится п запросов, что соответствует принятому обозначению Cn (t0). Пусть в фиксированный момент времени Δt в ИСМО поступил еще один запрос. Этому состоянию будет соответствовать обозначение Cn+1 (t0+Δt). Если за такой же момент времени Δt завершено решение одной из задач (вопросов), то состояние ИСМО примет обозначение Cn-1 (t0+Δt). Следовательно, марковскую последовательность процессов изменения состояний ИСМО, определяемых увеличением числа задач путем поступления информации по соответствующему закону распределения и уменьшения количества задач в системе путем выдачи пользователям результатов (ответов) решения, можно записать в виде марковских цепей соответственно увеличения и уменьшения вопросов (задач) в ИСМО:
Сn → (t0 )→Cn+1 (t0 +Δt); Δt→0; (17.72) Cn(t0)→Cn-1(t0+Δt); Δt→0.
Для марковских последовательностей состояний увеличения и уменьшения (17.72) запишем вероятность перехода ИСМО соответственно в состояние увеличения и уменьшения:
Pn{Cn(t0)→Cn+1(t0+Δt)}=μn,n+1Δt+0(Δt);
Pn+1{Cn+1(t0)→Cn(t0+Δt)}=μn+1,nΔt+0(Δt). (17.73)
Вероятность того, что в момент Δt в ИСМО не поступит ни одной задачи, примет вид
Pn{Cn(t0)-/→Cn+1(t0+Δt)}=1-μn,n+1Δt+0(Δt). (17.74)
Таким образом, в процессе функционирования ИСМО может находиться в (n+i)-м состоянии с соответствующими ему вероятностями P0 (t), P1 (t), P2 (t), ..., Pn (t) Pn+1 (t), i =1,k, сумма которых всегда равна единице и которые можно определить, задавая интенсивности входных потоков информации λij и выходных потоков обслуженных вопросов (задач) μij. Подробный вывод дифференциальных уравнений Колмогорова-Эрланга, по которым легко определяются все вероятности любых состояний, изложен в специальной литературе. Однако для стационарного состояния можно предложить более простой способ расчета вероятностей состояний ИСМО на основе использования
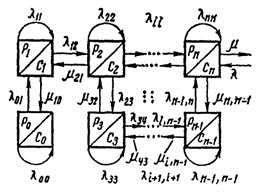
Рис.17.1.Схема размеченного марковcкого графа состояний однотерминальной ИСМО
415
теории размеченных графов. С этой целью вернемся к рис. 17.1, на котором представлена марковская цепь последовательностей состояний ИСМО в виде размеченного графа, квадраты которого представляют состояния и их вероятности в соответствии с системой (17.69), а стрелки - соответственно входные и выходные потоки, переводящие ИСМО в состояние увеличения или уменьшения номеров последовательности марковской цепи в соответствии с системами (17.70) и (17.71). Исключив зависимости состояний и вероятностей от времени, примем установившееся состояние функционирования ИСМО, которое можно описать линейными однородными алгебраическими уравнениями на основе использования размеченного графа. В соответствии с системой (17.69) и графом марковской цепи установившегося режима ИСМО запишем линейное алгебраическое уравнение, сбалансированное по нулю, для состояния С0:
Р0λ00 + P1μ10 - P0λ00 - P0λ01 = 0.(17.75)
Аналогично запишем сбалансированные уравнения соответственно для состояний С1, С2, С3, ..., Сn-1, Сn размеченного графа ИСМО:
Р0λ01 + P1λ11+P2μ21-P1μ10-P1λ11-P1λ12=0;
P1λ12+P2λ22+P3μ32-P2μ21-P2λ22-P2λ23=0;
P2λ23+P3λ33+P4μ43-P3μ32-P3λ33-P3λ34=0; (17.76)
.................
Pn-1λn-2,n-1+Pn-1λn-1,n-1+Pnμn,n-1-Pn-1μn-1,n-2-
-Pn-1λn-1,n-1-Pn-1λn-1,n=0.
Так как в стационарном режиме работы ИСМО λii всех состояний равны нулю, сделав соответствующие преобразования, выражения (17.75) и (17.76) перепишем в виде одной системы из n+1 уравнений с п неизвестными Рi, коэффициентами которых являются λij и μij:
|
λ01 P0+0-μ10 |
P1-0=0; |
λ01 |
P0+μ21 P2-μ10 |
P1-λ12 P1=0; |
λ12 |
P1+μ32 P3-μ21 |
P2-λ23 P2=0; (17.77) |
λ23 |
P2+μ43 P4-μ32 |
P3-λ34 P3=0; |
........................
λn-2,n-1 Pn-2+μn,n-1 Pn-μn-1,n-2Pn-1-
-λn-1,n Pn-1= 0.
Решив систему (17.77) и учитывая, что
n
∑
i=0
Pi = 1, определим вероятность первоначального состояния ИСМО:
P0=1/
n
∑
k=0 k
∏
j=1
(λj-1,j/μj,j-1).(17.78)
Зная вероятность Р0 и подставляя ее в каждое из уравнений (17.77), находим все остальные вероятности состояний ИСМО, представленных в виде размеченного
416
графа на рис. 17.1. Если интенсивности λij, переводящие ИСМО в состояния увеличения (i<j), и интенсивности обслуживания (решения) задач μij, переводящие систему в состояния уменьшения (i>j) при стационарном режиме работы последней, принять постоянными, то общую формулу для вычисления всех Pi можно записать в виде:
Pi=
i
∏
k=1
ηk[
n
∑
k=0 k
∏
i=1
ηj] -1.(17.79)
Коэффициент η является относительной интенсивностью входного потока информации (задач, вопросов и др.) и как один из основных параметров ИСМО определяет производительность и эффективность использования ее технических и программных ресурсов. Фактически λ/μ=η представляет собой среднее число задач (вопросов), поступающее в ИСМО за средний интервал времени решения (обслуживания) одной задачи (ответа). Если за среднее время принять его математическое ожидание M(tотв), то
η=λM(tотв), (17.80)
где М(tотв)=1/μ.
Таким образом, при установившемся режиме функционирования ИСМО по выражениям (17.78) и (17.79) определяются предельные значения вероятностей состояний системы. Необходимо еще определить все вероятности при конкретных начальных условиях, для чего зададим последние и запишем
n
∑
i=0 (17.81)
Pi(t)=P0(t)/t=0+P1(t)/t=0+P2(t)/t=0+...+Pn(t)/t=0 = = P0(0)+P1(0)+P2 (0)+...+Pn(0) = 1.
Очевидно, в начальный момент времени (t=0) состояния системы и их вероятности с учетом выражения (17.69) можно представить следующим образом:
С0 (0)→Р0 (0) = 1;
(17.82)
С1 (0)→Р1 (0) = 0;...Сn (0)→Pn (0) = 0.
Определив начальные и предельные вероятности состояний ИСМО, перейдем к расчету основных характеристик эффективности ее функционирования. Пусть Р0 (0) =1 и система исправна, имеет стопроцентную готовность к эксплуатации задач, все остальные вероятности при заданных начальных условиях Рi (0), где i {1,n} равны нулю - в системе не решается ни одна задача. Следовательно, при начальных условиях Pi(t) является функцией от t и 0 < i ≤n, а предельная вероятность Pn(t) является вероятностью того, что в момент t в ИСМО поступит информация по (n+1)-й задаче, что фактически является отказом в решении (n+1)-й задачи, т.е. Рот ≈ Pn+1 (t) ≈ Рn (t),тогда. вероятность противоположного события Q10(t) = 1 - Pn(t) является относительной пропускной способностью ИСМО, которую определим для предельных состояний (t→∞) системы
417
Q10 =1-
n
∏
k=1
ηk[
n
∑
k=0 k
∏
j=1
ηj]-1. (17.83)
Поскольку Q10 является фактически отношением количества решенных задач или выданных ответов ко всему количеству поступивших задач или вопросов за принятую единицу времени, номинальную (проектную) пропускную способность ИСМО получим в результате произведения Q10 и интенсивности λ, т.е.
Q1н=Q10λ. (17.84)
В ИСМО может поступать неограниченное число вопросов и задач. Очевидно, в этом случае сроки их решения могут и не соблюдаться ввиду того, что по своим техническим параметрам ИСМО не может в определенную единицу пропустить сверхнормативное количество информации. Приведем данные анализа производительности ИСМО и ее загрузки.
Коэффициент |
Соотношения |
|
Сроки ответов или |
|
производительности |
интенсивностей |
Загрузка ИСМО |
||
решения задач |
||||
ИСМО |
потоков |
|
||
|
|
|||
|
|
|
|
|
η=0 |
λ=μ =0 |
Простой |
Не определены |
|
|
|
|
|
|
η<1 |
λ<μ |
Недозагрузка |
Соблюдаются |
|
|
|
|
|
|
η=1 |
λ=μ |
Номинальная |
Соблюдаются |
|
загрузка |
||||
|
|
|
||
|
|
|
|
|
η>1 |
λ>η |
Перегрузка |
Задерживаются |
|
|
|
|
|
Теперь определим, сколько может находиться задач, вопросов и т.д. в очереди.
Для ИСМО, реализующей обработку алфавитно-цифровой информации свыше 1 млрд. АЦЗ в год, многофазовая система оперативного мультипрограммирования обеспечивает рациональное распределение программных, аппаратных и трудовых ресурсов однотерминальной ИСМО, сокращает время ожидания и обслуживания задач, способствует сокращению сроков и повышению качества их решения. Пусть допустимое число задач, находящихся в ИСМО на решении, представляет собой случайную величину Н, принимающую только целочисленные значения, закон распределения которой известен и задан в виде табл. 17.2.
|
|
|
|
|
|
Таблица 17.2 |
|
|
|
|
|
|
|
Hi |
h0 |
h1 |
h2 |
... |
hn-1 |
hn |
|
|
|
|
|
|
|
|
0 |
1 |
2 |
... |
n-1 |
n |
|
|
|
|
|
|
|
Pi |
P0 |
P1 |
P2 |
... |
Pn-1 |
Pn |
|
|
|
|
|
|
|
|
- |
- |
- |
... |
- |
- |
|
|
|
|
|
|
|
Так как дискретная случайная величина Н принимает конечное множество значений, ее математическое ожидание М(Н) можно определить по формуле:
M(H)=
n
∑
i=0
hi Pi=
n
∑
i=0
iPi=n. (17.85)
418
По этой формуле определяется среднее число задач, которые могут находиться в ИСМО. С учетом формулы (17.85) окончательно получим выражение для определения среднего количества вопросов или задач1 в системе
n=
n
∑
i=0 i
∏
k=1
ηk/
n
∑
k=0 k
∏
j=1
ηj. (17.86)
Величина n может принимать различные значения при разных значениях величины ηi заданной в области значений действительных чисел (1≥ηi >0). В момент t0+Δt(Δt→0) вероятность того, что в ИСМО находится на решении, хотя бы одна задача в соответствии с выражением (17.78) будет равна
PΔt (n>0)=1-[
n
∑

k=0 k
∏
j=1
(λj-1,j /μj,j-1 )] -1 .(17.87)
Теперь определим среднее количество вопросов (задач), которые могут попасть в портфель заказов и ожидать в очереди. Так, если в ИСМО всего п задач и в некоторый момент (Δt)R задач решается, то в портфеле заказов будет N задач, т.е.
N = n-R. (17.88)
Рассчитаем среднее время нахождения одной задачи в ИСМО по следующей формуле:
Tc= n/λ. (17.89)
Определим среднее время нахождения каждой из задач, ожидающих в очереди:
ТK=N/λ. (17.90)
С учетом формул (17.89) и (17.90) получим среднее время решения ИСМО одной задачи, которое представляет собой разницу между средним временем пребывания в ИСМО одной задачи и средним временем нахождения информации (вопроса, задачи) в очереди:
tp =Tc-TK.(17.91)
Таким образом, изложенная методика позволяет определить следующие характеристики однотерминальной ИСМО:
предельные вероятности, определяющие наличие вопросов или задач в системе или их отсутствие, относительный коэффициент загрузки системы, относительную пропускную способность (производительность); номинальную
419
(проектную) пропускную способность; соблюдение или несоблюдение сроков решения задач, время простоя ИСМО; процент недозагрузки или загрузки системы; среднее количество решаемых и ожидающих решения задач; среднее время решения одной задачи; среднее время нахождения одной задачи (ожидающей запуска на решение) в очереди; общее время нахождения в ИСМО задач, вопросов и др.
420
1 Если h не ограничено и интенсивности (λ,μ) переходов ИСМО из состояния в состояние постоянны,
то n =
∞
∑
i=0
(i-n)iηi
413 :: 414 :: 415 :: 416 :: 417 :: 418 :: 419 :: 420 :: Содержание 420 :: 421 :: 422 :: 423 :: 424 :: Содержание
17.6. Методика расчета многотерминальной ИСМО
Рассмотрим модель МИСМО, заданную выражением (17.68) и работающую по принципу on-line при n=2, 3, 4,...,m в режиме разделения времени. Представим марковскую последовательность состояний системы:
C'0 - МИСМО исправна, ни одной задачи и ни одного вопроса в ней нет; С'1– на одном из m терминалов с центральным ядром системы работает один пользователь; C'2 - занято два терминала, а остальные m-2 свободны; С'3 - занято три терминала, остальные m-3 свободны и т.д.; C'j - j- терминалов занято, остальные свободны; С'm - все терминалы заняты и в МИСМО находятся на обслуживании (решении) m задач (вопросов).
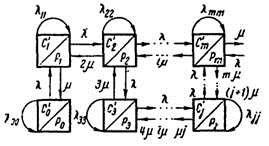
Схема графа отмеченных состояний приведена на рис 17.2. По методике, изложенной в предыдущем параграфе, для размеченного графа составим сбалансированные по нулю линейные однородные алгебраические уравнения для всех т состояний МИСМО. После соответствующих преобразований и с учетом установившегося режима многотерминальной сети имеем
Рис 17.2. Схема размеченого марковского графа m- терминальной ИСМО (i <j)
μP1-λP0 = 0; λP0-(λ+μ)P1+2μP2=0;
λP1-(λ+2μ)P2+3μP3=0
λP2-(λ3μ)P3+4μP4=0;
λP3-(λ+4μ)P4+5μP5=0;
(17.92)
......................
λPj-[λ(j+1)μ]Pi+1+(j+2)μPj+2=0;
......................
λPm-2-[λ+(m-1)μ]Pm-1+mμPm=0;
λPm-1-mμPm=0.
Решив систему (17.92), получим следующие формулы для вычисления вероятностей, отвечающих состояниям МИСМО, приведенной на рис. 17.2:
420
P1=(λ/μ)P0;P2=(λ2/2μ2)P0;...;Pj=(λ j/j!μ j)P0;... (17.93)
