Выделение проблем и постановка задачи дипломной работы
Основная проблема, связанная с данной предметной областью заключается в отсутствии Оптимального планирования маршрутов передвижения водителей-экспедиторов. Время, затрачиваемое им на перемещение от точки к точке оказывает немаловажное влияние на общее количество торговых точек, посещаемых за день. При полном отсутствии формальных механизмов Оптимального планирования маршрутов, которое, как мы выяснили имеет место, сложно говорить об эффективном перемещении водителей-экспедиторов. В итоге компания может не до конца использовать потенциал своих сотрудников, тратить лишние деньги на оплату ГСМ и т.п.
Целью дипломной работы будет являться нахождение решения проблемы оптимального планирования маршрутов передвижения водителей-экспедиторов компании «Пепсико Холдингс» через реинжиниринг бизнес-процессов.
Достижение поставленной цели должно обеспечить:
Сокращение времени на перемещение между точками объезда.
Повышение количества торговых точек, которые может за один день посетить водитель-экспедитор;
Положительное изменение доходов компании за счет расширения клиентской базы и точек сбыта.
Моделирование и оптимизация деятельности водителя-экспедитора ооо «пепсико холдингс»
Математическая модель Оптимального планирования маршрутов передвижения водителя-экспедитора
Водителю-экспедитору необходимо, выехав из офиса ООО «Пепсико Холдингс», посетить по разу в неизвестном порядке торговые точки и вернуться в офис. Расстояния между торговыми точками известны. В каком порядке следует обходить города, чтобы замкнутый путь водителя-экспедитора был кратчайшим?
Маршрут в графе – это последовательность вершин x1, x2… xn, такая, что для каждого i=1, 2… n−1 вершины xi и xi+1 соединены ребром. Эти n−1 ребер называются ребрами маршрута. Говорят, что маршрут проходит через них, а число n−1 называют длиной маршрута. Говорят, что , если маршрут соединяет вершины xi и xn, то они называются соответственно началом и концом маршрута, вершины x2…x n называются промежуточными. Маршрут называется замкнутым, если x1=xn.
Путь – это маршрут, в котором все ребра различны. Путь называется простым, ес-ли и все вершины в нем различны.
Цикл – это замкнутый путь. Цикл x1, x2… xn-1, x1 называется простым, если все вер-шины x1, x2… xn-1 попарно различны [9].
Установим некоторые простые свойства маршрутов.
В любом маршруте, соединяющем две различные вершины, содержится простой путь, соединяющий те же вершины. В любом цикле, проходящем через некоторое ребро, содержится простой цикл, проходящий через это ребро.
Если в графе степень каждой вершины не меньше 2, то в нем есть цикл. Доказательство этих свойств можно найти в [9].
Расстоянием между двумя вершинами графа называется наименьшая длина пути, соединяющего эти вершины. Расстояние между вершинами a и b обозначается через d(a,b). Если в графе нет пути, соединяющего a и b, то расстояние между ними считается бесконечным. Функция d(a,b) обладает следующими свойствами:
d(a,b)≥0, причем d(a,b)=0 тогда и только тогда, когда a=b;
d(a,b)=d(b,a);
d(a,b)+d(b,c)≥d(a,c) (неравенство треугольника).
Расстояние от данной вершины a до наиболее удаленной от нее вершины называется эксцентриситетом вершины a и обозначается через ecc(a). Таким образом, ecc(a)=max d(a,x). Вершину с наименьшим эксцентриситетом называют центральной, а вершину с наибольшим эксцентриситетом – периферийной. Множество всех центральных вершин называется центром графа. Сама величина наименьшего эксцентриситета называется радиусом графа и обозначается rad( G), а величина наибольшего – диаметром и обозначается diam(G) . Наименьший диаметр имеет полный граф (граф, все вершины которого попарно смежны) – его диаметр равен 1 [9].
Для ориентированного графа можно определить два типа маршрутов:
1) неориентированный маршрут – это чередующаяся последовательность x 1, e1, x2, e2… ek-1, xk вершин и ребер графа, такая, что для каждого i=1, 2… k−1 выполняется одно из
двух: ei=(xi, xi+1) или ei=(xi+1, xi);
2) маршрут называется ориентированным (или ормаршрутом), если ei=(xi, xi+1) для каждого i.
Таким образом , при движении вдоль неориентированного маршрута в орграфе ребра могут проходиться как в направлении ориентации, так и в обратном направлении, а при движении вдоль ормаршрута (или просто маршрута) – только в направлении ориентации. Это различие очевидным образом распространяется на пути и циклы, так что в орграфе можно рассматривать пути и орпути, циклы и орциклы. Определимся, что маршрут соединяет вершины xi и xk, а ормаршрут ведет из x i в xk. При решении задачи нахождения оптимального маршрута на графе можно выделить ряд известных и хорошо зарекомендовавших себя методов.
Поиск в глубину. Работа всякого алгоритма обхода состоит в последовательном посещении вершин и исследовании ребер . Какие именно действия выполняются при посещении вершины и исследовании ребра – зависит от конкретной задачи, для решения которой производится об-ход. В любом случае, факт посещения вершины запоминается, так что с момента посещения и до конца работы алгоритма она считается посещенной. Вершину, которая еще не посещена, будем называть новой. В результате посещения вершина становится открытой и остается такой, пока не будут исследованы все инцидентные ей ребра. После этого она превращается в закрытую [9].
Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин, такой, что каждая вершина просматривается в точности один раз. Поэтому важной задачей является нахождение хороших методов поиска в графе. Метод поиска хорош, если он позволяет алгоритму решения интересующей нас задачи легко использовать этот метод и каждое ребро графа анализируется не более одного раза (или количество таких исследований ограничено сверху) [11].
Поиск в глубину – это наиболее важная ввиду многочисленности приложений стратегия обхода графа. Идея этого метода – идти вперед в неисследованную область, пока это возможно, если же вокруг все исследовано, отступить на шаг назад и искать новые возможности для продвижения вперед. Метод поиска в глубину известен под разными названиями: «бэктрекинг», «поиск с возвращением» [9].
Обход начинается с посещения заданной стартовой вершины a, которая становится активной и единственной открытой вершиной. Затем выбирается инцидентное вершине a ребро (a, y) и посещается вершина y. Она становится открытой и активной. В дальнейшем, как и при поиске в ширину, каждый очередной шаг начинается с выбора активной вершины из множества открытых вершин . Если все ребра, инцидентные активной вершине x, уже исследованы, она превращается в закрытую. В противном случае выбирается одно из неисследованных ребер ( x, y), это ребро исследуется. Если вершина y новая, то она посещается и превращается в открытую.
При поиске в глубину в качестве активной выбирается та из открытых вершин, которая была посещена последней. Для реализации такого правила выбора наиболее удобной структурой хранения множества открытых вершин является стек : открываемые вер-шины складываются в стек в том порядке, в каком они открываются, а в качестве актив-ной выбирается последняя вершина [9].
Поиск в ширину
Поиск в ширину – это классический метод решения задачи нахождения кратчайшего пути между двумя конкретными вершинами графа. Кратчайший путь – это такой путь, соединяющий вершины графа, который обладает тем свойством, что никакой другой путь, соединяющий эти вершины, не содержит меньшее число ребер. Поиск в глубину мало пригоден для решения этой задачи, поскольку предлагаемый им порядок прохождения графа не имеет отношения к поиску кратчайших путей, а поиск в ширину предназначен как раз для достижения этой цели [12].
Итак, рассмотрим метод поиска в ширину. Отметим, что в рассмотренном в предыдущем разделе методе поиска в глубину чем позднее будет посещена вершина, тем раньше она будет использована – точнее, так будет при допущении, что вторая вершина посещается перед использованием первой. Это прямое следствие того факта, что просмотренные, но еще не использованные вершины скапливаются в стеке. Поиск в ширину, грубо говоря, основывается на замене стека очередью [11].
Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их удаленности от некоторой заранее выбранной или указанной стартовой вершины a. Иначе говоря, сначала посещается сама вершина a, затем все вершины, смежные с a, то есть находящиеся от нее на расстоянии 1, затем вершины, находящиеся от a на расстоянии 2, и далее по удаленности [9].
Рассмотрим алгоритм поиска в ширину с заданной стартовой вершиной a. Вначале все вершины помечаются как новые. Первой посещается вершина a, она становится единственной открытой вершиной. В дальнейшем каждый очередной шаг начинается с выбора некоторой открытой вершины x. Эта вершина становится активной. Далее исследуются ребра, инцидентные активной вершине . Если такое ребро соединяет вершину x с новой вершиной y, то вершина y посещается и превращается в открытую. Когда все ребра, инцидентные активной вершине, исследованы, она перестает быть активной и становится за-крытой. После этого выбирается новая активная вершина, и описанные действия повторяются. Процесс заканчивается, когда множество открытых вершин становится пустым.
Основная особенность поиска в ширину, отличающая его от других способов обхода графов, состоит в том, что в качестве активной вершины выбирается та из открытых, которая была посещена раньше других . Именно этим обеспечивается главное свойство поиска в ширину: чем ближе вершина к старту, тем раньше она будет посещена . Для реализации такого правила выбора активной вершины удобно использовать для хранения множества открытых вершин очередь – когда новая вершина становится открытой, она добавляется в конец очереди, а активная выбирается в ее начале [9].
Оба метода поиска в графе – в глубину и в ширину могут быть использованы для нахождения пути между фиксированными вершинами a и b. Достаточно начать поиск в графе с вершины a и вести его до момента посещения вершины b. Преимуществом поиска в глубину является тот факт, что в момент посещения вершины b стек содержит последовательность вершин, определяющую путь из a в b. Это становится очевидным, если отметить, что каждая вершина, помещаемая в стек, является смежной с предыдущей. Однако недостатком поиска в глубину является то, что полученный таким образом путь в общем случае не будет кратчайшим путем из a в b. От этого недостатка свободен метод нахождения пути, основанный на поиске в ширину [11].
Кратчайшие пути
В этом и 3 последующих разделах будем рассматривать ориентированные графы G=(V,E), дугам которых приписаны веса. Это значит, что каждой дуге (u,v) поставлено в соответствие некоторое вещественное число a(u,v), называемое весом данной дуги. Пола-гаем a(u,v)=∞, если дуга (u,v) не существует.
Под длиной пути будем понимать сумму весов дуг, из которых состоит путь. Длину кратчайшего пути будем обозначать d(s,t) и называть расстоянием от s до t. Если не существует ни одного пути из s в t, то полагаем d(s,t)=∞.
Введем еще одно ограничение. Путь веса дуг будут только положительными значениями. Так как при существовании дуг с отрицательными весами длина кратчайшего пути между парой вершин становится неопределенной, исходя из возможности неоднократного включения таких дуг в путь.
Зная расстояние между парой вершин, можно легко определить кратчайший путь. Так как для двух произвольных вершин s и t (s≠t) существует такая вершина v , что d(s,t )=d(s,v)+d(v,t). Этим свойством обладает и предпоследняя вершина в кратчайшем пути от s к t. Следовательно, определяя таким образом предпоследнюю вершину, можно пройти от конца кратчайшего пути к его началу [11].
Большинство известных алгоритмов нахождения расстояния между двумя верши-нами s и t можно описать следующей последовательностью действий.
При заданной матрице весов дуг A[u,v], вычисляем некоторые верхние ограничения D[v] на расстояния от s до всех вершин v.
Каждый раз, когда выясняется, что D[u]+A[u,v]<D[v], улучшаем оценку
D[v]=D[u]+A[u,v].
Процесс заканчивается, когда дальнейшее улучшение ни одного из ограничений не возможно. Значение каждой D[u] получается равным расстоянию d(s,u). Вершину s в данном случае называют источником.
Алгоритм нахождения расстояния от источника до всех вершин, реализующий вышеизложенные действия в общем случае ( при отсутствии контуров с отрицательной дли-ной) называется методом Форда-Беллмана [13].
Алгоритм Дейкстры для поиска кратчайшего пути
Алгоритм Дейкстры решает задачу нахождения кратчайших путей для единственного источника на ориентированных графах, имеющих неотрицательные веса. Он основан на методе поиска в ширину.
Работу алгоритма Дейкстры можно описать следующей последовательностью действий:
начинаем поиск путем помещения источника в просмотренную зону;
добавляем на каждом шаге одно ребро, дающее кратчайший путь из источника в вершину, не включенную в просмотренную зону; то есть вершины добавляются в про-смотренную зону в порядке возрастания их удаленности от источника.
Таким образом, чтобы найти кратчайший путь от s к t с помощью алгоритма Дейкстры, достаточно начать поиск с вершины s и закончить его, когда вершина t добавится в очередь [12].
Алгоритм обхода препятствий А*
Предлагаемый алгоритм обхода препятствий основан на алгоритме Дейкстры. В англоязычной литературе он называется алгоритмом A* («а»-звездочка) [14, 15].
Алгоритм реализуется в ряде предположений:
карта разбита на квадратные части, называемыми клетками (ячейками);
каждая клетка имеет несколько показателей:
стоимость прохождения по этой клетке,
предыдущая клетка – клетка, из которой пришли в эту клетку,
статус клетки (нерассмотренная, граничная, отброшенная),
оценка пройденного пути,
оценка оставшегося пути;
имеются две клетки – начальная и конечная;
сосед клетки – клетка, в которую можно попасть из рассматриваемой за 1 шаг.
Общий принцип: на каждой итерации из всех граничных точек выбирается та, для которой сумма уже пройденного пути и пути до конца по прямой является минимальной, и от нее осуществляется дальнейшее продвижение.
Алгоритм итерационный. Опишем реализацию алгоритма пошагово. Начальные данные: Start – начальная клетка, Finish – конечная клетка.
шаг. Помечаем Start как граничную точку.
шаг. Среди всех граничных точек находим Клетку1 – клетку с минимальной суммой оценки пройденного пути g и оценки оставшегося пути h.
шаг. Для Клетки1 рассматриваем соседей. Если сосед имеет статус нерассмотренного, то мы обозначаем его как граничную клетку, и указываем Клетку1 как предыдущую для него. Оценку g для соседа принимаем равной g+p, где p-стоимость прохождения по клетке-соседу, а g – оценка пройденного пути для Клетки1. Оценка h для любой клетки равна длине кратчайшего пути (количеству ячеек на пути по прямой от рассматриваемой клетки до клетки Finish). Рассматриваемую Клетку1 помечаем как отброшенную.
шаг. Если на предыдущем шаге один из соседей оказался равен клетке Finish, то путь найден. Если ни одного нового соседа не существует, то нет и пути.
шаг. Переход на шаг 2.
Алгоритм достаточно прост и в тоже время быстр. Он превосходит по скорости алгоритм Дейкстры (в общем случае) благодаря направленному поиску [14, 15].
Генетический алгоритм
Нейронные сети и генетические алгоритмы в настоящее время находят огромное число разнообразных применений. Действительно, в любой области человеческой деятельности есть задачи, для решения которых не существует определенного алгоритма или существующие алгоритмы очень сложны и требуют значительных вычислительных затрат, которые выходят за рамки возможностей современных ЭВМ. Нейронные сети и генетические алгоритмы являются универсальным средством для решения подобных задач, а также практически любых задач, которые возникают в человеческой деятельности [13].
В некоторых задачах, таких как прогнозирование, проектирование или распознавание образов, нейронные сети стали уже привычным инструментом. Ниже приведены не-которые из многочисленных способов использования нейронных сетей и генетических алгоритмов в различных областях [16]:
обслуживание кредитных карточек;
медицинская диагностика;
распознавание речи;
обнаружение фальсификаций;
анализ потребительского рынка;
прогнозирование объема продаж и управление закупками;
проектирование и оптимизация сетей связи;
прогнозирование изменений котировок;
управление ценами и производством;
разработка месторождений;
исследование факторов спроса;
прогнозирование потребления энергии.
Естественный отбор в природе
Эволюционная теория утверждает, что каждый биологический вид целенаправлен-но развивается и изменяется для того, чтобы наилучшим образом приспособиться к окружающей среде. В процессе эволюции многие виды насекомых и рыб приобрели защитную окраску, еж стал неуязвимым благодаря иглам, человек стал обладателем сложнейшей нервной системы. Можно сказать, что эволюция – это процесс оптимизации всех живых организмов. Рассмотрим, какими же средствами природа решает эту задачу оптимизации.
Основной механизм эволюции – это естественный отбор. Его суть состоит в том, что более приспособленные особи имеют больше возможностей для выживания и размножения и, следовательно, приносят больше потомства, чем плохо приспособленные особи. При этом, благодаря передаче генетической информации (генетическому наследованию), потомки наследуют от родителей основные их качества. Таким образом , потомки сильных индивидуумов также будут относительно хорошо приспособленными , а их доля в общей массе особей будет возрастать. После смены нескольких десятков или сотен поколений средняя приспособленность особей данного вида заметно возрастает [16].
Чтобы сделать понятными принципы работы генетических алгоритмов, поясним также, как устроены механизмы генетического наследования в природе. В каждой клетке любого животного содержится вся генетическая информация этой особи. Эта информация записана в виде набора очень длинных молекул ДНК (дезоксирибонуклеиновая кислота). Каждая молекула ДНК – это цепочка, состоящая из молекул нуклеотидов четырех типов, обозначаемых А, T, C и G. Собственно, информацию несет порядок следования нуклеотидов в ДНК. Таким образом, генетический код индивидуума – это просто очень длинная строка символов, где используются всего 4 буквы. В животной клетке каждая молекула
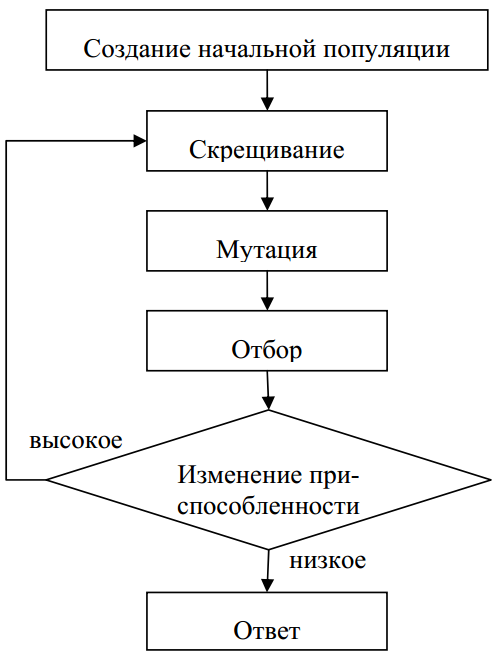
Рисунок 2.1 – Блок-схема работы генетического алгоритма
ДНК окружена оболочкой – такое образование называется хромосомой. Каждое врожденное качество особи (цвет глаз, наследственные болезни, тип волос и т. д.) кодируется определенной частью хромосомы, которая называется геном этого свойства . Например , ген цвета глаз содержит информацию, кодирующую определенный цвет глаз. Различные значения гена называются его аллелями.
При размножении животных происходит слияние двух родительских половых клеток и их ДНК взаимодействуют, образуя ДНК потомка. Основной способ взаимодействия – кроссовер (cross-over – скрещивание). При кроссовере ДНК предков делятся на две части, а затем обмениваются своими половинками. При наследовании возможны мутации из-за радиоактивности или других влияний, в результате которых могут измениться некоторые гены в половых клетках одного из родителей. Измененные гены передаются потом-ку и придают ему новые свойства. Если эти новые свойства полезны, они, скорее всего, сохранятся в данном виде – при этом произойдет скачкообразное повышение приспособленности вида [16].
Понятие и особенности генетического алгоритма
Пусть дана некоторая сложная функция (целевая функция), зависящая от нескольких переменных, и требуется найти такие значения переменных, при которых значение функции максимально. Задачи такого рода называются задачами оптимизации и встречаются на практике очень часто.
Генетический алгоритм – это простая модель эволюции в природе, реализованная в виде компьютерной программы. В нем используются как аналог механизма генетического наследования, так и аналог естественного отбора. При этом сохраняется биологическая терминология в упрощенном виде. Вот как моделируется генетическое наследование:
• хромосома – вектор (последовательность) из нулей и единиц. Каждая позиция (бит) называется геном;
• индивидуум (генетический код) – набор хромосом, вариант решения задачи;
• кроссовер – операция, при которой две хромосомы обмениваются своими частями;
мутация – случайное изменение одной или нескольких позиций в хромосоме.
Чтобы смоделировать эволюционный процесс , сгенерируем вначале случайную популяцию – несколько индивидуумов со случайным на-бором хромосом (числовых векторов). Генетический алгоритм имитирует эволюцию этой популяции как циклический процесс скрещивания индивидуумов и смены поколений.
Жизненный цикл популяции – это несколько случайных скрещиваний (посредством кроссовера) и мутаций, в результате которых к популяции добавляется какое-то количество новых индивидуумов. Отбор в генетическом алгоритме – это процесс формирования новой популяции из старой, после чего старая популяция погибает. После отбора к новой популяции опять применяются операции кроссовера и мутации, затем опять происходит отбор, и так далее (рис. 2.1).
Отбор в генетическом алгоритме тесно связан с принципами естественного отбора в природе. Приспособленность индивидуума – значение целевой функции на этом индивидууме. Популяция следующего поколения формируется из наиболее приспособленных особей. Чем больше приспособленность индивидуума, тем больше вероятность его участия в кроссовере, то есть размножении.
Таким образом, модель отбора определяет, каким образом следует строить популяцию следующего поколения. Как правило, вероятность участия индивидуума в скрещивании берется пропорциональной его приспособленности. Часто используется так называемая стратегия элитизма, при которой несколько лучших индивидуумов переходят в следующее поколение без изменений, не участвуя в кроссовере и отборе. В любом случае каждое следующее поколение будет в среднем лучше предыдущего. Когда приспособленность индивидуумов перестает заметно увеличиваться, процесс останавливают и в качестве решения задачи оптимизации берут наилучшего из найденных индивидуумов [16].
Итак, если на некотором множестве задана сложная функция от нескольких переменных, то генетический алгоритм – это программа , которая за разумное время находит точку, где значение функции достаточно близко к максимально возможному. Выбирая приемлемое время расчета, мы получим одно из лучших решений, которые вообще воз-можно получить за это время.
Алгоритм решения задачи коммивояжера
Рассмотрим применение генетических алгоритмов в классической задаче коммивояжера (TSP – travelling salesman problem). Суть задачи состоит в том, чтобы найти кратчайший замкнутый путь обхода нескольких городов, заданных своими координатами. Оказывается , что уже для 30 городов поиск оптимального пути представляет собой сложную задачу, побудившую развитие новых различных методов (в том числе нейросетей и генетических алгоритмов).
Каждый вариант решения такой задачи – это числовая строка, где на j-ом месте стоит номер j-ого по порядку обхода города. Таким образом, в этой задаче столько пара-метров, сколько городов в сети, причем не все комбинации значений допустимы. Естественно, первой идеей является полный перебор всех вариантов обхода. Но такой подход к решению задачи абсолютно невозможен при современных ЭВМ. Если в задаче все города связаны с каждым из остальных, то количество разных вариантов решения задачи (N−1)!/2, где N – количество городов в сети. При N=30 число вариантов решения 4,4×1030. Для перебора этих вариантов понадобится много времени! И это только при 30 городах, когда как в практике задачи такого рода насчитывают сотни, и даже тысячи городов. В таких ситуациях на помощь приходят генетические алгоритмы, которые, хотя и не гарантируют нахождение оптимального решения, но позволяют найти одно из приемлемых решений задачи [16].
Построение генетического алгоритма начинается с конструирования двоичной хромосомы, представляющей возможные решения этой задачи. Традиционно генетические алгоритмы используют для этого двоичные строки фиксированной длины. Предположим, что задана сеть из 4-х городов, для кодирования каждого из которых понадобится 2 бита. Таким образом, хромосома будет иметь длину 1 байт. Например: «01_10_11_00».
Если следовать справа налево, то данная хромосома предполагает маршрут 0-3-2-1. Очевидно, что такой подход к построению хромосомы не из лучших, потому что может получиться так, что один город окажется в маршруте не один раз, что противоречит зада-че. Подойдем к этой проблеме несколько иначе. Пусть число на j-ом месте означает не номер следующего города в маршруте, а номер города из оставшихся (не пройденных) городов. Так для нашего примера сначала 0-вой город, затем число 3 (11) показывает номер следующего города из оставшихся 1,2,3 (для 1-ого города номер 0, для 2 – 1 и для 3 – 2), так как число 3 превышает максимальный номер из оставшихся, то будем использовать вместо него остаток от деления его же на число оставшихся городов: 3 mod 3 = 0, то есть следующим городом в маршруте будет оставшийся город с номером 0, то есть 1-ый город, и так далее. Таким образом, при данном подходе не будет иметь место ситуация, когда один город окажется в маршруте не один раз. Заметим, что число на последнем месте хромосомы (самое левое) вовсе не нужно, так как остается один город (после прохождения трех), кодировать который нет необходимости. И еще важная поправка к хромосоме, заключается в том, что для кодирования очередного города необходимо не то количество бит, которое необходимо для хранения общего числа городов, а то, которое достаточно для кодирования числа оставшихся городов. Например, хромосома «01_10_11_00» преобразуется к виду (для того же маршрута) «1_10_00».
В результате мы уменьшили размер хромосомы с 8 бит до 5, что, во-первых, позволяет сэкономить оперативную память, во-вторых, уменьшить число возможных вариантов решения задачи (а также исключить невозможные «решения»). Второе качество является очень важным, так как эффективность генетического алгоритма тем выше, чем ниже число вариантов решения. Если одни города не имеют связи с некоторыми другими, то это также сокращает число вариантов решения.
Следующий этап построения генетического алгоритма – разработка так называемой фитнес-функции. Эта функция является единственной частью программы, которая должна понимать то, что действительно кодирует хромосома, и возвращать число, которое можно сопоставить с выживаемостью индивидуума в природе. Используя эту функцию, мы можем определить, насколько хорошо приспособлен индивидуум (насколько длинный маршрут). Так как количественной характеристикой решения в нашей задаче является длина пути, то примем в качестве значения фитнес-функции выражение «1/длина пути» (чем выше длина маршрута, тем ниже приспособленность).
Сначала генерируется определенное количество хромосом со случайными значениями (это количество обычно несколько сотен или тысяч) . Результатом данного этапа является создание начальной популяции. Далее реализуется жизненный цикл популяции (случайное скрещивание, мутация) и отбор. Продолжать это нужно либо определенное количество раз (сотни, тысячи раз), или до тех пор, пока приспособленность не будет значительно изменяться.
Для каждой пары хромосом определяется случайным образом, будут ли они скрещиваться. Операция кроссовера предполагает выбрать также случайным образом, точку кроссовера. После этого две хромосомы обмениваются старшими частями(слева от точки кроссовера).
Например, даны две хромосомы: «10111» и «01100». Точка кроссовера может быть 1, 2, 3 или 4 (исходя из размера хромосомы – 5 бит). Пусть случайным образом определена точка 2, таким образом, хромосомы преобразуются в другие (рис. 2.2).
Рисунок. 2.2 – Кроссовер хромосом
Дальнейший этап – это мутация. Частота мутации обычно очень низкая – отвечающая за нее виртуальная монетка должна падать орлом вверх один раз за сто или тысячу бросаний. А суть мутации заключается в том, что в некоторой хромосоме инвертируется некоторый бит.
И, наконец, происходит отбор индивидуумов в следующее поколение. Для реализации этой операции представим себе виртуальную рулетку, но такую, у которой секторы неодинаковые по ширине. Каждый сектор будет соответствовать какой-либо хромосоме, а ширина его будет пропорциональна приспособленности индивидуума. Теперь запустим рулетку столько раз, сколько индивидуумов в популяции. Та особь, на которую укажет остановившийся шарик, переходит в следующее поколение. Таким образом, шансы у наиболее приспособленных выше, чем у других, и в среднем число «хороших» решений будет расти с каждым очередным поколением.
Далее снова выполняем скрещивание, мутацию и отбор, и так далее до определенного условия. Этим условием может быть малое изменение приспособленности с каждым поколением или его отсутствие, либо процесс эволюции продолжается определенное количество раз (сотни, тысячи, возможно миллионы). И в самом конце выбираем особь с наибольшей приспособленностью . Это решение и будет максимально близким среди найденных к оптимальному решению задачи [16].
Важно отметить, что во всех этих операциях присутствует случайность, что необходимо для генетического алгоритма. Это повышает вариабельность решений.