8.Градиент и его свойства.

Пусть в каждой точке некоторой области задана функция. Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функциии обозначаетсяили(читается «набла у»):.

При этом говорят, что в области определено векторное поле градиентов.

Для нахождения градиента функции в заданной точкеиспользуют формулу:.

 

Свойства градиента

1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление векторасовпадает с направлением градиента. Это наибольшее значение производной равно.

2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю

11.Таблица неопределенного интеграла.

   где

15.Интегрирование иррациональных функций.

Интегрирование некоторых иррациональных функций

Интеграл вида 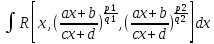, гдеR – рациональная функция, а p1, q1, p2, q2 – целые числа, находят с помощью подстановки , гдеn – наименьшее общее кратное q1, q2

Интеграл 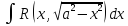, гдеR – рациональная функция, находят подстановкой x=a, интеграл – подстановкойx=a tg t, а интеграл 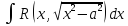– подстановкойx=

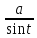
Найти множество первообразных функции .

Решение.

Правило интегрирования и таблица первообразных сразу приводят нас к ответу:

Ответ:

.

18.Определенный интеграл и его геометрический смысл.

Определенный интеграл на отрезке есть число равное пределу интегральных сумм при стремлении к нулю шага разбиения отрезка

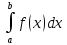
Сумма произведений f(называетсяинтегральной суммой для функции на отрезке

Шагом разбиения отрезка называется наибольшая длина отрезков деления

Площадь, ограниченная непрерывными кривыми y=f1(x), y=f2(x), вертикалями x=a, x=b, где f1(x)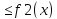 при a,вычисляется по формуле

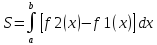
Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой и прямыми, равен

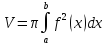
Объем тела, образованного вращением вокруг оси Oy криволинейной трапеции, ограниченной непрерывной кривой и прямыми, равен

22.Нахождение площадей плоских фигур и объемов тел вращения с помощью интегралов..

Криволинейной трапецией называется плоская фигура, ограниченная осью , прямыми, и графиком непрерывной на отрезке функции , которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:

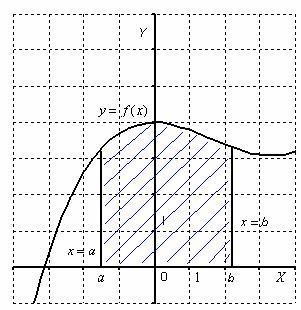
Тогда площадь криволинейной трапеции численно равна определенному интегралу .

С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.  То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Например, рассмотрим определенный интеграл . Подынтегральная функциязадает на плоскости кривую, располагающуюся выше оси(желающие могут выполнить чертёж), а сам определенный интегралчисленно равен площади соответствующей криволинейной трапеции.

Пример 1

Вычислить площадь фигуры, ограниченной линиями ,,,.

Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа. Причем, чертеж необходимо построить ПРАВИЛЬНО. 

При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. Графики функций выгоднее строить поточечно, с техникой поточечного построения можно ознакомиться в справочном материале Графики и свойства элемент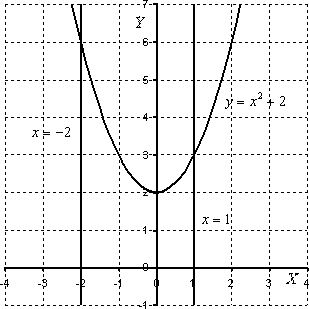арных функций. Там же можно найти очень полезный применительно к нашему уроку материал – как быстро построить параболу.

В данной задаче решение может выглядеть так. Выполним чертеж (обратите внимание, что уравнение задает ось

Штриховать криволинейную трапецию я не буду, здесь очевидно, о какой площади идет речь. Решение продолжается так:

На отрезке график функциирасположен над осью, поэтому:

Ответ: