36. Формула Беиса.

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события

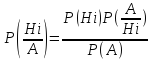–ФОРМУЛА БАЙЕСА

39. Дискретная случайная величина и ее табл. Распределения.

Дискретной случайной величиной называется такая величина, которая в результате опята может принимать определенные изолированные значения с некоторой вероятностью.

Соотношение между возможными значениями случайной величины и их вероятности называется законом распределения дискретной случайной величины.

Пусть случайная величина Х задана таблицей распределения

Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений на соответствующие вероятности:

Математическое ожидание называют также средним значением случайной величины Х, подчеркивая статистический смысл понятия, или центром распределения случайной величины Х (по аналогии с понятием центра тяжести для системы материальных точек).

Свойства математического ожидания:

1)     если случайная величина Х принимает постоянное значение Х=С= =const, то М(С)=С;

2)     М(СХ)=СМ(Х), С = const;

3)     Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: M(X+Y)=M(X)+M(Y);

4)     Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M(X×Y)=M(X)×M(Y).

Наряду с характеристиками положения большую роль играют характеристики рассеяния. Рассеяние случайной величины Х связано с отклонением этой величины от ее центра распределения М(Х). Чтобы учитывать отклонения противоположных знаков, удобно рассматривать квадраты отклонений.

Дисперсией D(X) случайной величины Х называют средний квадрат отклонения случайной величины от ее центра распределения:

Используя свойства математического ожидания, можно записать более удобную формулу для подсчета дисперсии

.

Для того, чтобы рассматривать отклонение в тех же единицах, что и значения случайной величины, вводится еще одна характеристика – среднее квадратическое отклонение s(Х), которое определяется как

.

Свойства дисперсии:

1)       D(X) ³ 0; 2)       если С=const, то D(С) = 0;

3)       ,С=const;

4)       D(X ± Y) = D(X) + D(Y).

Пример. Дискретная случайная величина Х задана таблицей распределения:

 

Х

2

3

5

6

Р

0,5

0,2

0,2

0,1

 

Найти М(Х), D(X), s(X).

Решение. Найдем математическое ожидание: М(Х)=2×0,5+3×0,2+5×0,2+6×0,1=3,2.

Дисперсию вычислим по формуле .

;

;

42.Свойства мат. Ожидания.

1. Матем. ожидание постоянной величины равно самой постоянной М(С)=С

2. Постоянный множитель можно выносить за знак матем. Ожидания М(Сх)=СМ(х)

3. Матем. Ожидание произведения 2 независимых случайных величин равно произведению их матем. ожиданий М(ху)=М(х)М(у)

Матем. ожидание отклонения случайной величины от ее матем. ожидания равно нулю М(х-М(х))=0

Свойство  1.  Математическое  ожидание  по­стоянной величины равно самой постоянной: М(С) = С.

Свойство 2.   Постоянный множитель можно выно­сить за знак математического ожидания: М(СХ) = СМ(Х).

                                                 

Для понимания последующих свойств дополнительно введем несколько комментарий

Две случайные величины называют независимыми,если закон распределения одной из них не зависит от того, какие воз­можные значения приняла другая величина. В противном случае случайные величинызависимы. Несколько случайных величин назы­вают взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

Произведение независимых случай­ных величин Xи Y можно определить как случайную величину XY,возможные зна­чения которой равны произведениям каждого возможного значения X на каждое возможное значение У; вероятности возможных значе­ний произведения XY равны произведениям вероятностей возможных значений сомножителей. Причем некоторые произведения  могут оказаться рав­ными между собой. В этом случае вероятность возможного значения произведения равна сумме соответствующих вероятностей.

 Свойство 3. Математическое ожидание произведе­ния двух независимых случайных величин равно произведе­нию математических ожиданий сомножителей

M(XY) = M(X)·M(Y). Следствие. Математическое ожидание произведе­ния нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Например, для трех случайных  величин имеем:

М (XYZ) = М (XY ·Z) = M (XY) M(Z)=M (X) ·М (Y) · М(Z).

Для произвольного числа случайных величин дока­зательство проводится методом математической индукции.

 Свойство 4. Математическое ожидание суммы (разности) двух случайных величин равно сумме их математических ожиданий слагаемых. Математическое ожидание разности двух случайных величин равно разности  их математических ожиданий слагаемых.

M(X+Y) = M(X) + M(Y); M(X-Y) = M(X)-M(Y)

Эти свойство также распространяется на любое количество событий