1.Функция двух переменных и ее график. Элипсоид,парабалоид,гиперболойд.

Переменная называется функция двух переменных, если каждой паре чисел из некоторого множества по определенному правилу или закону ставится в соответствии одно или несколько значений.

Графиком функции называется поверхность, представляющая собой геометрическое место точек, когда точка принимает все значения из области определения.

Линией уровня функции называют геометрические места, при которых функция принимает одно и тоже значение С.

Поверхностью уровня функции называется поверхность, в точках которой функция сохраняет значение, равное С.

Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида: .

Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.

Гиперболоид— это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением - (однополостный гиперболоид), где a и b — действительные полуоси, а c — мнимая полуось; или- (двуполостный гиперболоид), где a и b — мнимые полуоси, а c — действительная полуось.

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

4. Непрерывность функции двух переменных. Точки разрыва.

Число А называется пределом функции при перемещении точки М к М0, если для каждого числа 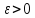найдется такое число 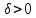, что для всех точек М, для которых верно условиеMM0<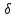(), выполняется неравенство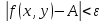

Записывают:

Функция называется непрерывной в точке, если

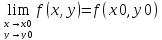
Геометрически это означает, что при приближении точки М по любой последовательности точек к точке М0 аппликаты соответствующих точек поверхности, изображающих функцию стремятся к аппликате поверхности точки.

Точки разрыва функции – это точки, в которых функция имеет разрыв, при этом функция в этих точках не является непрерывной. Существует определенная классификация точек разрыва функции. Точки разрыва функции делятся на точки разрыва первого рода и точки разрыва второго рода.

    

Точки разрыва первого рода при x=a имеют место быть, если существуют левосторонний и правосторонний пределы: lim(x→a-0)⁡f(x) и lim(x→a+0)⁡f(x). Эти пределы должны быть конечны. Если хотя бы один из односторонних пределов равен нулю или бесконечности, то в таком случае функция имеет точки разрыва второго рода.

7.Дифференциал функции двух переменных.

Функция называется дифференцируемой в точке, если ее полное приращение можно представить в виде

Приращение называется полным приращением функции в точке, соответствующим приращением 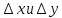независимым перемещением

10.Понятие первообразной функции и неопределенного интеграла.

Функция F (х) называется первообразной функцией для  данной функции f (х) (или, короче, первообразной данной функции f (х)) на данном промежутке, если на этом промежутке  . Пример. Функцияявляется  первообразной функциина всей числовой оси, так какпри любом х.  Отметим, что вместе с  функциейпервообразной дляявляется любая функция вида, где С —  произвольное постоянное число (это следует из того, что производная постоянной равна нулю). Это свойство имеет место и в общем случае.

Теорема 1. Если и— две  первообразные для функции f (х) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.  Из этой теоремы следует, что если известна какая-нибудь первообразная F (х) данной  функции f (х), то все множество первообразных для f (х) исчерпывается функциями F (х) + С.  Выражение F (х) + С, где F (х) —  первообразная функции f (х) и С — произвольная  постоянная, называется неопределенным интегралом от функции f (х) и обозначается символом,  причем f (х) называется подынтегральной функцией ;— подынтегральным выражением,  х — переменной  интегрирования;  ∫ — знак неопределенного интеграла.  Таким образом, по определениюесли.  Возникает вопрос: для всякой ли функции f (х) существует первообразная, а значит, и  неопределенный интеграл?  Теорема 2. Если функция f (х) непрерывна на [a ; b], то на этом отрезке для функции f (х) существует первообразная.  Ниже мы будем говорить о первообразных лишь для непрерывных функций. Поэтому  рассматриваемые нами далее в этом параграфе  интегралы существуют.