6.Производная по направлению и ее вычисления.

Предел отношения приназывается производной от функциив точкепо направлению вектораи обозначается, т.е..

Производная по направлению характеризует скорость изменения функции в направлении вектора. Если то функциявозрастает в направлении вектора, если, то функцияубывает в направлении вектора.

Механический (физический) смысл производной по направлению состоит в том, что она характеризует мгновенную скорость изменения функции в точкевнаправлении вектора.

Для вычисления производной по направлению функции двух переменных используют формулу:

где инаправляющие косинусы, т.е. косинусы углов, образуемых векторомс осями координат.

Пример.. Найти производную функции в точкев направлении, идущем от этой точки к точке

Решение. Вычислим иНайдем значения этих производных в точке:Найдем координаты вектораВычислим направляющие косинусы вектораДля вычисления производной функциипо направлениюподставим полученные выражения в формулу: 

9.Экстремум функции двух переменных. Условия экстремума.

Функция имеет максимум (минимум) в точкеМ0, если для любой точки М, находящейся в некоторой окрестности точкиМ0, выполняется условие f(x0, y0)>f(x, y) (f(x0, y0)<f(x, y)).

Максимумы и минимумы функции называются экстремумами.

Теорема (необходимое условие экстремума) Если функция-дифференцируемая функция и достигает в точке М0 экстремума, то ее частные производные первого порядка в этой точке равны нулю.

Точки, в которых частные производные первого порядка обращаются в нуль (или не существуют), называются критическими или стационарными.

; ;

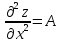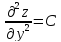
Дискриминант .

Достаточное условие экстремума в стационарной точке:

1. –экстремум есть, при этом, если А>0 (или С>0 при А=0), в точке функция имеет минимум, а если А<0 (или C<0 при А=0) – максимум

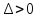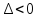2. –экстремума нет

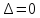–требуется дополнительные исследования

13. Интегрирование по частям в неопред. Интеграле

12.Замена переменной в неопределенном интеграле.

Интегрирование по частям

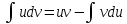
  Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:      а) , где  – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае: ;      б) , где U – новая переменная. Формула замены переменной при такой подстановке: .

16.Интегрирование квадратичных иррациональностей.

R(x, √ a2 ± x2 )  и  R(x, √ x2 − a2 )

где R — рациональная функция.

а) Для интегрирования выражений R(x, √ a2 − x2 ) используются подстановки

x = a · sin t     или     x = a · cos t .

б) Для интегрирования выражений R(x,√a2 − x2 ) dx используются подстановки

x = a · tg t     или     x = a·sht .

в) Для интегрирования выражений R (x,√a2 − x2 ) dx используются подстановки

  x= a/cost   или     x=a·ch t .

Во всех случаях, применив формулу замены переменной в неопределенном интеграле, получаем интегралы вида

∫ Rs(sin t, cos t) dt ,

где Rs — рациональноя функция, т.е. задача сводится к интегрированию триглнометрических выражений.

19.Замена переменной в определенном интеграле.