45.Распределение Паусона и ее характеристики.

Говорят, что случайная величина  распределена по закону Пуассона, если вероятность того, что она примет определенное значение, выражается формулой 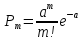, где а – некоторая положительная величина, называемая параметром закона Пуассона.

При больших n и малых р вычисления по формуле Бернулли затруднены. В этих случаях обычно используют формулу Пуассона , ,

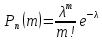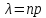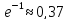
Дискретная случайная величина имеет распределение Пуассона с параметром λ, если:

Распределение Пуассона также называется распределением редких событий.

Распределение Пуассона - это дискретное распределение, являющееся одним из важных предельных случаев биномиального распределения

48. нормальное распределение как одно из важнейших распределений непрерывности случайной величины. Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равнагдеm - математическое ожидание случайной величины; σ² - дисперсия случайной величины, характеристика рассеяния значений случайной величины около математического ожидания. Условием возникновения нормального распределения являются формирование признака как суммы большого числа взаимно независимых слагаемых, ни одно из которых не характеризуется исключительно большой по сравнению с другими дисперсиями. Нормальное распределение является предельным, к нему приближаются другие распределения. Математическое ожидание случайной величины Х. распределено по нормальному закону, равно m_x = m, а дисперсия D_x = σ². Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервале (α, β) выражается формулойгде - табулированная функция

51.Центральная предельная теорема Ляпунова.

Если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то случайная величина имеет распределение близкое к нормальном

Закон больших чисел устанавливает условия, при которых среднее значение случайной величины стремится к некоторой постоянной, при стремлении числа испытаний к бесконечности. Существует группа теорем, которая описывает условия стремления закона распределения случайной величины к нормальному. Одна из таких теорем - теорема Ляпунова. Данная теорема устанавливает некоторые условия, при которых закон распределения суммы Yn = X1 + X2 + ... + Xn случайных величин при стремлении n к бесконечности стремится к нормальному закону распределению. Рассмотрим эти условия: если есть независимые случайные величины X1, X2, X3 ... и каждая из этих величин имеет математическое ожидание М(Хi) и дисперсию D(Xi), абсолютный центральный момент третьего порядка bi и предел отношениястремится к нулю, то закон распределения суммы этих величин при стремлении n к бесконечности приближается к нормальному закону распределения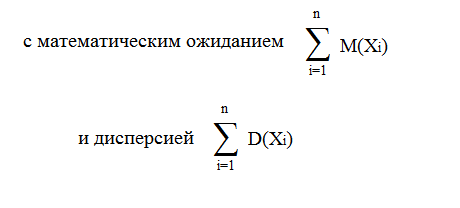

54. Точечные методы оценивания неизвестных параметров.

Точечные оценки. Свойства оценок.

Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называют ее точечной статистической оценкой

Точечное оценивание применяют для приблизительной оценки параметров генеральной совокупности по статистиками выборки наблюдений выборочные показатели статистическим оценкам параметров генеральной совокупности с определенной точностью (или с определенными статистическими погрешностями) К в того же статистические оценки являются случайными величинами, обладающими неконтроное разброс даже если выборки взяты из той же генеральной совокупности.

При оценке желательно, чтобы потеря информации, которая может быть существенной для принятия статистических решений, была минимальной Итак, для того, чтобы оценки были надежными, они должны отвечать некоторым требование ам, т.е. обладать определенными свойствами.

Основными свойствами статистических оценок является способность, незмищеннисть, эффективность:

o Возможность Статистическая оценка ®_n состоянии, когда при постоянном увеличении объема выборки (n - \"со) она приближается к значению параметра ©, который оценивает Статистика ©\" способную оценке параметpa 0, когда для любого добавляют атного числа есть есть справедливо соотношениеввідношення

o Незмищеннисть Статистика считается несмещенной, если ее математическое ожидание равно параметру, оценивается Выборочное среднееX является несмещенной оценке генерального среднего fi, поскольку м [X]= ц чего нельзя сказать, например, о выборочных показатели дисперсии

o Эффективность Точечная оценка называется эффективной, если она имеет наименьшую степень дисперсии выборочного распределения по сравнению с аналогичными оценками, т.е. обнаруживает наименьшую случайную вариативность