
- •4. Непрерывность функции двух переменных. Точки разрыва.
- •7.Дифференциал функции двух переменных.
- •10.Понятие первообразной функции и неопределенного интеграла.
- •14. Интегрирование рациональных функций.
- •17.Нахождение интегралов с помощью уравнений
- •21.Интеграл с переменной верхней границей как первообразная для подинтегральной функции. Формула Ньютона-Лейбница.
- •24.Теорема существования и единственности сущ. Решения д.У. 1порядка задача Коши.
- •27. Однородное д.У. И его решение.
- •33. Вероятность суммы событий.
- •34. Вероятность суммы независимых событий.
- •37. Формула Бернулли.
- •40. Функция распределение случайной величины и ее свойства.
- •43. Свойство дисперсии.
- •46. Геометрическое распределение и ее характеристики.
- •49. Формула Лапласа для определения вероятностей для нормального распределения.
- •52. Понятие случайной выборки и статистического ряда.
- •55. Интервальные методы.
- •8.Градиент и его свойства.
- •11.Таблица неопределенного интеграла.
- •15.Интегрирование иррациональных функций.
- •18.Определенный интеграл и его геометрический смысл.
- •22.Нахождение площадей плоских фигур и объемов тел вращения с помощью интегралов..
- •Нахождение объемов тел вращения с помощью интегралов
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
- •Как вычислить объем тела вращения?
- •25. Д.У. С разделяющимися переменными и метод его решения.
- •28.Основные понятия комбинаторики: перестановка, размещение и сочетание….
- •31.Геометрическая вероятность.
- •35.Полная группа событий. Формула полной вероятности.
- •38. Наивероятнейшее число в схеме Бернулли.
- •41. Числовые характеристики случайной величины.( мат. Ожидание, дискрет.Величниа)
- •44. Биноминальное распределение и ее характеристики.
- •50.Теорема Чебышева. Закон больших чисел.
- •53. Выборочная средняя исправленная выборочная дисперсия.
- •58. Двусторонняя критическая область.
- •6.Производная по направлению и ее вычисления.
- •9.Экстремум функции двух переменных. Условия экстремума.
- •13. Интегрирование по частям в неопред. Интеграле
- •12.Замена переменной в неопределенном интеграле.
- •16.Интегрирование квадратичных иррациональностей.
- •19.Замена переменной в определенном интеграле.
- •20.Интегрирование по частям в опред. Интервале.
- •23.Дефференциал уравнения и его общее и частное решение и их геометрическая интерпритация.
- •26.Линейное д.У. 1порядка и метод его решения.
- •29. Основные понятия теории вероятности: испытание, событие и вероятность.
- •32. Условная вероятность. Вероятность произведения события.
- •36. Формула Беиса.
- •39. Дискретная случайная величина и ее табл. Распределения.
- •45.Распределение Паусона и ее характеристики.
- •51.Центральная предельная теорема Ляпунова.
- •54. Точечные методы оценивания неизвестных параметров.
- •57. Односторонняя критическая область
- •60. Уравнение линии регрессии.
- •2 Типа взаимосвязей между х и у:
- •59. Статистическое и корреляционная зависимость случ. Вел.
- •56. Статистическая обработка результатов наблюдения с помощью критерия согласия.
41. Числовые характеристики случайной величины.( мат. Ожидание, дискрет.Величниа)
Дисперсией
дискретной случайной величины
называется матем. ожидание квадрата
отклонения случайной величины от ее
матем. ожидания. D(x)=M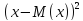
Теорема.
Дисперсия
равна разности между матем.ожиданием
квадрата случайной величины и квадратом
ее матем.ожидания D(x)=M(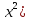 -
-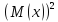
Теорема. Дисперсия числа появления события А в n независимых испытаний, в каждой из которых вероятность р появления собития постоянна, равно произведению числа испытаний на вероятности появления и непоявления события в каждом испытании D(x)=npq
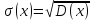 –среднее
квадратичное отклонение
–среднее
квадратичное отклонение
Коэффициент
вариации—
это отношение стандартного отклонения
к среднему арифметическому, выраженное
в процентах.
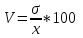
Математическим
ожиданием дискретной случайной величины
называется
сумма произведений всех возможных
значение случайной величины на их
вероятности.
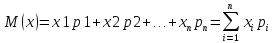
Теорема. Матем. ожидание числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании М(х)=nр
44. Биноминальное распределение и ее характеристики.
Случайная
величина, принимающая значение
с
вероятностями
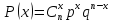 ,
где i=0,
1, 2,..., n,
q=1-р,
0<p<1,
называется биномиально
распределенной случайной величиной
,
где i=0,
1, 2,..., n,
q=1-р,
0<p<1,
называется биномиально
распределенной случайной величиной
Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.
Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:
![]()
где pn - вероятность того, что при n испытаниях событие А наступит n раз;
qn - вероятность того, что при n испытаниях событие А не наступит ни разу;
![]() -
вероятность того, что при n испытаниях
событие А наступит m раз, а
событие Āнаступит n-m раз;
-
вероятность того, что при n испытаниях
событие А наступит m раз, а
событие Āнаступит n-m раз;
![]() - число
сочетаний (комбинаций) появления
события А и Ā.
- число
сочетаний (комбинаций) появления
события А и Ā.
Числовые характеристики биноминального распределения:
М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;
D(m)=npq - дисперсия частоты появления события. А;
![]() - среднее
квадратическое отклонение частоты.
- среднее
квадратическое отклонение частоты.
50.Теорема Чебышева. Закон больших чисел.
Неравенство Чебышева.
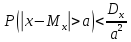 –неравенство
Чебышева.
–неравенство
Чебышева.
Это
неравенство позволяет оценить вероятность
того, что
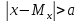
Теорема Чебышева.
Пусть
имеется конечная последовательность
независимых случайных величин с одним
и тем же матем.ожиданием и дисперсиями,
ограниченными одной и той же постоянной.
Тогда каково бы ни было положительное
число а, вероятность события
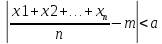 стремиться к единице при n
стремиться к единице при n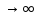
Изучение статистических закономерностей позволило установить, что при некоторых
условиях суммарное поведение большого количества случайных величин почти утрачи-
вает случайный характер и становится закономерным (иначе говоря, случайные отклоне-
ния от некоторого среднего поведения взаимно погашаются). В частности, если влияние
на сумму отдельных слагаемых является равномерно малым, закон распределения суммы
приближается к нормальному. Математическая формулировка этого утверждения дается в
группе теорем, называемой законом больших чисел
47.Гипергеометрическое
распределение.
Пусть
задано некоторое множество однотипных
элементов, число которых равно N;
из них K элементов
имеют, например, признак А (цвет,
стандартность, наполнения), а
остальные N-K элементов
- признак В.
С этого множества наугад берут n еэлементов.
Случайная величина X –
число элементов с признаком вида А, что
случается среди n наугад
взятых элементов. Тогда X принимает
значения k=0,1,2,...,min(n,K) ,
а вероятность их появления определяется
гипергеометрическим законом распределения![]()
![]() В
табличной форме записи этот закон
распределения имеет вид
В
табличной форме записи этот закон
распределения имеет вид
![]() Напомним,
что сочетание находим по формуле
Напомним,
что сочетание находим по формуле![]() а факториал функцию по правилу–
а факториал функцию по правилу– ![]() При n=k
і k=0 сочетание
равное единице.
При n=k
і k=0 сочетание
равное единице.![]() Условие нормировки для
гипергеометрического распределения
имеет вид
Условие нормировки для
гипергеометрического распределения
имеет вид![]() В зависимости
от условия задачи наименьшее значение
может составлять m
= 0, 1, 2, 3, ..., m.
Числовые
характеристики этого закона вычисляются
по приведенным ниже формулам:
1.
Математическое ожидание
В зависимости
от условия задачи наименьшее значение
может составлять m
= 0, 1, 2, 3, ..., m.
Числовые
характеристики этого закона вычисляются
по приведенным ниже формулам:
1.
Математическое ожидание
![]()
2. Дисперсия и среднее квадратическое отклонение
![]()
![]()
3. Для асимметрии
![]()
и эксцесса
![]()
