37. Формула Бернулли.

Предположим, что несколько одинаковых машин в одних и тех же условиях перевозят груз. Любая машина может выйти из строя при этих перевозках. Пусть вероятность выхода из строя одной машины не зависит от выхода из строя других машин. Это значит, что рассматриваются независимые события (испытания). Вероятности выхода из строя каждой из этих машин примем одинаковыми ().

Пусть, в общем случае, производится независимых испытаний. Ставится задача определения вероятности того, что ровно в испытаниях наступит событие , если вероятность наступления этого события в каждом испытании равна . В случае с машинами это могут быть вероятности выхода из строя ровно одной машины, ровно двух машин и т.д.

Определим вначале вероятность того, что в первых испытаниях событие наступит, а в остальных испытаниях — не наступит. Вероятность такого события может быть получена на основании формулы вероятности произведения независимых событий

,

где .

Так как рассматривалась только одна из возможных комбинаций, когда событие произошло только в первых испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из элементов по , т.е. .

Таким образом, вероятность того, что событие наступит ровно в испытаниях определяется по формуле

, (3.3)

где .

Формула (3.3) носит название формулы Бернулли.

Пример. В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке известна и равна 0,5. Какова вероятность выигрыша ровно трех предметов?

Решение. По формуле Бернулли находим

40. Функция распределение случайной величины и ее свойства.

Функцией распределения случайной величины называют функцию, определяющую вероятность того, что случайная величина в результате испытания примет значение меньшее.

Свойства функции распределения:

1. Если функция распределения случайной величины, то значение функции распределения принадлежат отрезку

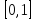
2. Функция распределения случайной величины – неубывающая функция F(x2)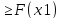приx2>x1

3. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна 0

4. Если функция распределения случайной величины, то

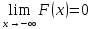
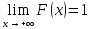
Вероятность того, что случайная величина примет значение, заключенное в интервале равна приращению функции распределения на этом интервале

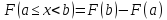
43. Свойство дисперсии.

Для большей наглядности обозначим дисперсию как D(X).

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю). D(A) = 0.

Оно и не удивительно – у постоянной величины нет отклонений.

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² (А в квадрате) раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X).

Данное свойство вполне очевидно, если вспомнить, что при расчете дисперсии отклонения от средней возводятся в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X).

Это свойство также вполне понятно, т.к. все значения и их среднее увеличиваются на одну и ту же величину, и при взятии их разностей, величина А просто сокращается.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y).

Выводится просто, учитывая второй способ расчета дисперсии и свойство математического ожидания.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y).

Здесь учитывается то, что дисперсия всегда положительна (все отклонения от средней возводятся в квадрат).