14. Интегрирование рациональных функций.

Интегрирование рациональных функций

Выражени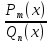е , где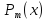,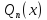– многочленыm-й и n-й степени соответственно, называется рациональной дробью (или функцией). Рациональная дробь называется правильной, если m<n, и неправильной, если m

Если подынтегральная дробь неправильная, нужно путем деления выделить частное и остаток от деления

Если знаменатель правильной дроби разлагается на множители 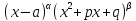…, то справедливо следующее разложение: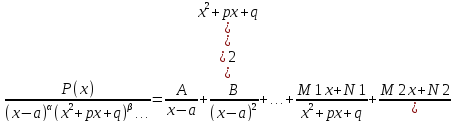

Вычислить интеграл .

Решение.

17.Нахождение интегралов с помощью уравнений

21.Интеграл с переменной верхней границей как первообразная для подинтегральной функции. Формула Ньютона-Лейбница.

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Для нахождения значения определённого интеграла 

найдём первообразную для подынтегральной функции , вычислив неопределённый интеграл:

Поскольку нас интересует любая первообразная, то мы можем взять (с тем же успехом могли взять и, и, и т.  п., но вид первообразной припроще, а постоянные сласаемые всё равно взаимно уничтожатся при вычислении подстановки). Итак, берёми вычисляем подстановку, беря в ней пределы равными пределам интегрирования:

Получаем, что

Теорема. Производная от интеграла по верхней границе равна подынтегральной функции, в которой переменная интегрирования заменена верхней границей:

Доказательство. Для нахождения производной функции  дадим  приращение  Тогда новое значение функции будет равно

Следовательно, приращение функции  при переходе из точки  в точку  окажется равным

Но, так как по свойству аддитивности

то

Применим к последнему интегралу теорему о среднем:

где с заключено между  Таким образом, приращение  функции  равно 

Согласно определению производной, имеем

Так как  то  а следовательно, и с стремятся к  Согласно условию, подынтегральная функция  непрерывна в точке L Поэтому

Следовательно,

что и требовалось доказать.

Теорема о производной интеграла по верхней границе является одной из основных теорем математического анализа. Эта теорема вскрывает глубокую связь между операциями определенного интегрирования и дифференцирования. Теорема о производной интеграла по верхней границе показывает, что функция  является первообразной для.  Но интеграл существует для любого значения  в силу теоремы существования определенного интеграла от непрерывной функции.

24.Теорема существования и единственности сущ. Решения д.У. 1порядка задача Коши.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную функцию и производные до n-ого порядка этой функции

Задача Коши. Отыскание решения дифференцируемого уравнения, удовлетворяющего заданным начальным условием, является важной задачей теории дифференцируемых уравнений.

Теорема Коши (существование и единство решения дифференцируемого уравнения 1 порядка разрешенного относительно производной). Если функция непрерывна на некоторой области плоскости и имеет в этой области непрерывную частную производную, то какова ни была бы точка (х0, у0) области, существует, и при том, единственное решение уравнения.

Теорема. Пусть функция и ее частная производная непрерывны в некоторой области D на плоскости xOy . Тогда, если точка принадлежит этой области, существует, и притом единственное, решение уравнения , удовлетворяющее начальному условию .

Геометрически это означает, что через каждую точку области D проходит одна и только одна интегральная кривая рассматриваемого уравнения. Данная теорема называется теоремой существования и единственности решения дифференциального уравнения .