20.Интегрирование по частям в опред. Интервале.

Замена переменных

Пусть выполняются следующие условия:

1. Функция непрерывна на отрезке

2. Функция непрерывна вместе со своей производной на отрезке

3. Функция определена и непрерывна на отрезке

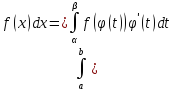
Интегрирование по частям

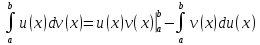
23.Дефференциал уравнения и его общее и частное решение и их геометрическая интерпритация.

Общее и частное решение

Общим решением дифференциального уравнения первого порядка называется решение, зависящее от одной произвольной постоянной C, придавая конкретное значение которой , можно получить решение , удовлетворяющее любому заданному начальному условию .

Равенство вида , неявно задающее общее решение, называется общим интегралом дифференциального уравнения. Заметим, что в практике чаще всего бывает нужным не общее решение, а так называемое частное решение,отвечающее определенным начальным условиям, вытекающим из условия данной конкретной задачи. Частным решением называется любая функция , которая получается из общего решения ,если в последнем произвольной постоянной C придать определенное значение. Соотношение называется в этом случае частным интегралом. 

26.Линейное д.У. 1порядка и метод его решения.

Уравнение вида a(x)y’+a0(x)y=b(x) называется линейным дифференциальным уравнение первого порядка

y’+p(x)y=q(x)

Для его решения применяется метод вариации произвольных постоянных. Предположим, что правая часть равна 0. Тогда y’+p(x)y=0 является уравнением с разделяющимися переменными:

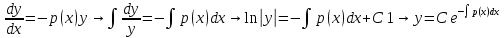
Для решения линейного уравнения можно так же применить подстановку y=uv. Тогда уравнение примет вид: 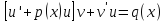. Если потребовать, что бы выражение в квадратных скобках было равно нулю, то найдемu(x), затем найдем v,а, следовательно, найдем y.

Y’+p(x)y=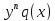, гдеn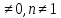 – уравнение Бернулли. Данное уравнение приводится к линейному с помощью подстановки z=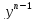

Уравнение

,

где и 

- заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Если функция , стоящая в правой части уравнения, тождественно равна нулю, т.е. ,  то уравнение называется линейным однородным, в противном случае - линейным неоднородным.  Таким образом, - линейное однородное уравнение, а - линейное неоднородное уравнение.

29. Основные понятия теории вероятности: испытание, событие и вероятность.

За вероятность события А принимается отношение числа благоприятствующих этому событию элементарных исходов (m) к общему числу возможных исходов (n): P(A)=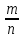

Событием называется всякое явление, которое может произойти или не произойти в результате опята

Опытом или испытанием называется всякое осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление.

32. Условная вероятность. Вероятность произведения события.

Вероятность произведения 2 событий равна произведению вероятности одного из них на условную вероятность второго относительно первого: P(AB)=P(A)P(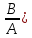=P(B)P(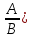

Для независимых событий вероятность их произведения равна произведению вероятностей этих событий. P(AB)=P(A)P(B)

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Вероятность события А, Вычисленная при условии, что произошло событие В, Называется Условной вероятностью события А при наличии события В И обозначается Р (А|В).

Вероятность произведения двух событий А И В, Равна произведению вероятности одного из этих событий на условную вероятность другого при наличии первого:

Р(АВ) = Р(А)Р(В|А) или Р(АВ) = Р(В)Р(А|В). (2.1)

Эта теорема обобщается на любое конечное число событий следующим образом: