5.2 Basic Principle

M elements in an array and m elements in each subarray, the overlap implies that M ≤ 2m. For subarrays that do not overlap, M = 2m.

The individual elements of each subarray can have arbitrary polarization, directional gain, and phase response, provided that each has an identical twin in its companion subarray. Elements of each pair of identical sensors, or doublet, are assumed to be separated physically by a fixed displacement (translational) vector. The array thus possesses a displacement (translational) invariance (i.e., array elements occur in matched pairs with identical displacement vectors). This property leads to the rotational invariance of signal subspaces spanned by the data vectors associated with the spatially displaced subarrays; the invariance is then utilized by ESPRIT to find DOAs. We will detail these concepts in the following section.

5.2.1Signal and Data Model

Assume d signals impinging onto the array. Let x1(t) and x2(t) represent the signal received by the two subarrays corrupted by additive noise n1(t) and n2(t). Each of the subarrays has m elements. From Section 2.2.1, the signals received can then be expressed as

where x1(t) and x2(t) are the m × 1 vectors representing the data received by the first and second subarrays, respectively. n1(t) and n2(t) are the m × 1 vectors representing the noises received by the two subarrays, respec-

tively. A = [a(μ ), …, a(μ )] is the m × d steering matrix of the subarray.

1 d [ ]

s(t) is the signals received by the first subarray. Φ = diag e j μ1 , , e j μd is

a d × d diagonal matrix that relates the signals received by the two subarrays and is called the rotation operator. It is caused by the fact that the signals arriving at the second subarray will experience an extra delay

84 Introduction to Direction-of-Arrival Estimation

Given N snapshots, x(t1), x(t2), …, x(tn), the objective of the ESPRIT technique is to estimate the DOAs via an estimation of μi by determining Φ = diag[e j μ1 , , e j μd ]. In doing so, two steps are required

based on the data received by the array: estimating the signal subspace and then estimating the subspace rotation operator [1–3]. They are further elaborated in Section 5.2.2.

5.2.2Signal Subspace Estimation

For a single signal, if x(t) = a(θ)s(t) (i.e., in the ideal noise-free situation), the data is confined to a one-dimensional subspace of CM characterized by the steering vector a(θ). For the d signals, the observed data vectors x(t) = As(t) are constrained to d-dimensional signal subspace of CM called the signal subspace (as described in Section 2.6). The objective here is to estimate this d-dimensional signal subspace. Let E1 and E2 denote two sets of vectors that span the same signal subspace, which is also ideally spanned by the columns of A. The signal subspace can be obtained from an array output covariance Rxx as explained in Section 3.3.3. The data covariance matrix Rxx has the following form:

~

Both Rss and the steering matrix A are assumed to have a full rank d.

Suppose that the signal subspace is spanned as E = [e , …, e ]. Since R

~ s 1 d ss

has a full rank, Es spans the same space as A. As a result, there must exist a unique nonsingular matrix T such that

~

E s = AT

Equation (5.5) basically indicates that the two subarrays span the same signal subspace and have the same dimension; this is because they are identically configured. As a result, a nonsingular d × d matrix denoted as 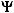can be found such that

As can be seen now, and 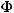are related via an eigenvalue-preserv- ing similarity transformation. The diagonal elements (or eigenvalues) of are equal to eigenvalues of the matrix that maps (rotates) the m-dimensional signal subspace matrix E1 associated with the first subarray to the m-dimensional signal subspace matrix E2 associated with the second subarray. In other words, the shift-invariance property is now expressed in terms of signal eigenvectors that span the signal subspace. Therefore, in ESPRIT, instead of finding the spatial rotational directly, we find the subspace rotating operator and then its eigenvalues that contain the DOA information.

5.2.3Estimation of the Subspace Rotating Operator

In a practical situation, only a finite number of noisy data are received

be solved exactly. Therefore, an approach needs to be developed to obtain