2. Линеаризация

Линеаризованные УУС получаются путём разложения в ряд Тейлора исходной системы (K.47):

B_{r n} v_n1 + W_r1 = 0_{r 1}. (K.14)

Коэффициенты B_{r n}, неизвестные v_n1 и свободные члены W_r1 этих уравнений традиционно записываются так:

, (K.49)

v_1n^T = (v₁, v₂, … v_n), (K.50)

W_1r^T = (w₁, w₂, … w_r). (K.51)

В алгебраической форме линеаризованные УУС имеют вид:

. (K.52)

Важнейшим моментом второго этапа является определение допустимости свободных членов («невязок») линеаризованных УУС.

Допустимые значения невязок УУС.

Вектор невязок W_r1 вычисляется по данным измерений y_n1 и координатам опорных точек z_q1:

Изучив статистические свойства векторов-оценивателей коррелатной версии, мы установили, что: E(W) = 0; а K_W = N. Из последнего факта следует, что , т.е. среднее квадратическое значение j-ой невязки – это диагональный элемент матрицы коэффициентов нормальных уравнений коррелат, находящийся на пересечении j-ой строки и j-ого столбца.

Установление допустимости невязки w _j начинается с проверки нулевой гипотезы о равенстве нулю её МО:

H₀ = {E(w_j) = 0} (K.53)

против альтернативной гипотезы

H_A = {E(w_j) ≠ 0}. (K.54)

Нулевая гипотеза (K.53) проверяется с помощью теста

t_Э = | w_j |/σ_{w j}, (K.55)

который сопоставляется на уровне значимости α с квантилью t_T распределения Стьюдента, характеризующегося r = n – k степенями свободы:

t_T = arg(F_Ст.^(n-1)= (1–α/2)). (K.56)

Воспользовавшись неравенством альтернативной гипотезы (K.54), получаем такое выражение для допустимого значения невязки j-го УУС:

t_Э = | w_j |/σ_wj ≤ t_T → w_j^доп = t_T* σ_wj = t_T*. (K.57)

Квантиль распределения Стьюдента, называемая «доверительным множителем», часто заменяется квантилью нормального распределения на том же уровне значимости. Нормальные доверительные множители, соответствующие уровням значимости 0.05, 0.01 и 0.003 равны:

t_0.05 = 1.96 ≈ 2; t_0.01 = 2.58 ≈ 2.6; t_0.003 = 3. (K.58)

Если вычисленная невязка лежит в допустимых пределах, это не означает, что она найдена без ошибок. К сожалению, не существует прямых контрольных выражений для проверки вычисления невязки. Выход один – вычисления «во вторую руку».

3. Нормализация

Нормальные уравнения коррелат в матричной форме имеют вид:

N_{r r}*Λ_r1 – W_r1 = 0_r1. (K.20)

Коэффициенты нормальных уравнений представляют собой произведение двух ранее введённых матриц:

N_{r r} = B_{r n} K_{n n} B^T_{n r}. (K.21)

Выполняя умножение данных матриц с учётом (K.48) и (K.49), получаем традиционную алгебраическую форму записи коэффициентов нормальных уравнений коррелат для случая некоррелированных измерений:

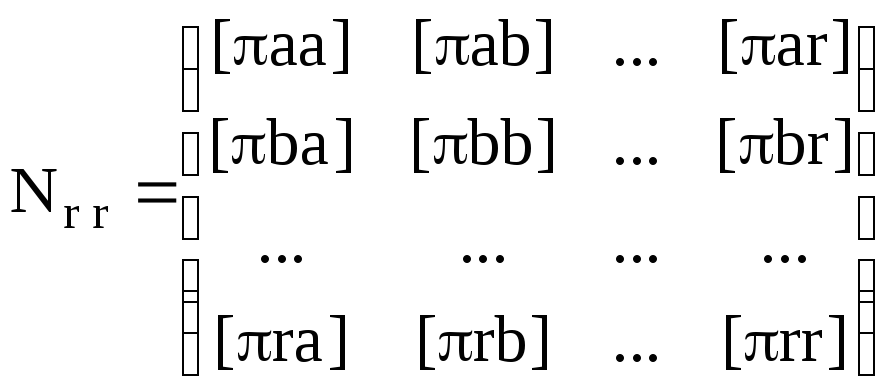. (K.59)

Свободные члены НУ коррелат (K.51) переносятся из линеаризованных УУС. Вектор неизвестных (коррелат), записанный в строку, имеет вид:

Λ_1r^T= (λ₁ ₂ … _r). (K.60)

Теперь, выполняя умножение матрицы (K.59) на вектор коррелат (K.60) и вычитая из произведения вектор «невязок» (K.51), получаем алгебраическую запись системы НУ коррелат:

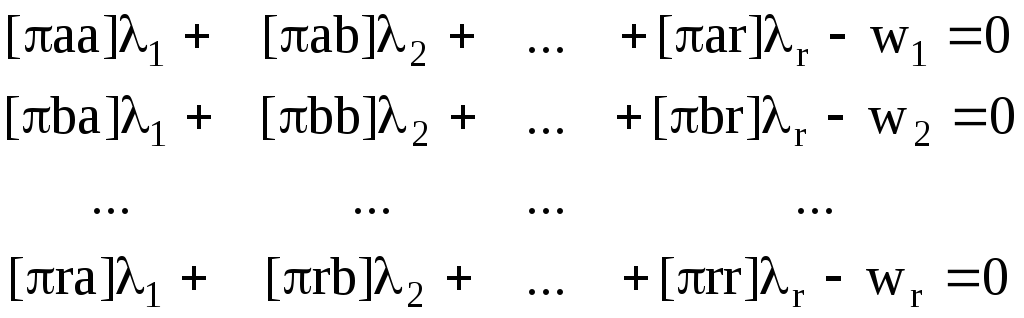
. (K.61)

4. Решение ну

Решение НУ коррелат, предлагаемое в теоретической части изложения материала, осуществляется методом обращения матрицы коэффициентов N_{r r} системы НУ (K.61):

L_{r 1} = N_{r r}^-1 W_{r 1}. (K.22)

Это сделано по следующим соображениям.

Во-первых, предполагая линейную независимость УУС, мы вправе считать, что матрица коэффициентов B_rn имеет полный строчный ранг, т.е. rank(B) = r. В таком случае матрица коэффициентов НУ N_{r r} = B_{r n} K B_nr^T будет иметь такой же ранг, и её определитель не будет равен нулю, т.е. det(N_{r r}) ≠ 0. Это означает, что существует N^-1 и решение системы (K.61) в форме (K.22).

Во-вторых, использование обратной матрицы N^-1 значительно упростило как уже выполненные теоретические выкладки, так и предстоящие преобразования.

В развёрнутом виде уравнения (K.22) можно записать, учтя тот факт, что обратная матрица коэффициентов нормальных уравнений является ковариационной матрицей коррелат, т.е. N_{r r}^-1 = K_Λ:

. (K.62)

Обратите внимание, что каждый диагональный элемент K_jj – это квадрат среднего квадратического значения j-ой коррелаты!

Отдельно j-ая строка системы (K.62) выглядит следующим образом:

 _j = K_{j 1}* w₁ + … +K_{j j}* w_j + … + K_{j r}* w_r. (K.63)

Выше уже отмечалось, что вычисление элементов K_ij обратной матрицы N^-1 через союзную матрицу на практике представляет собой трудоёмкую вычислительную задачу. Много проще реализовывать обращение с использованием различных алгоритмов решения СЛАУ.

В геодезии традиционно широко применяется алгоритм К.Ф.Гаусса, называемый «методом последовательного исключения неизвестных», и его модификации.

Суть метода Гаусса состоит в эквивалентной замене матрицы коэффициентов нормальных уравнений N_rr верхней треугольной матрицей U_rr (для сокращения записей обратные веса π опущены, что не влияет на сущность алгоритма). Эквивалентное преобразование реализуется путём последовательной замены строк исходной матрицы их линейными комбинациями друг с другом. Итак, матрица

(K.59)

преобразуется к верхнему треугольному виду

. (K.64)

Получаемая эквивалентная СЛАУ

(K.65)

легко решается в обратном порядке:

. (K.66)

Коррелаты Λ_1r^T = (₁, ₂, … _1r) вычисленные методом обращения или методом Гаусса, либо каким-то другим способом, должны быть проконтролированы. Такой контроль осуществляется путём подстановки найденных корней в исходную систему НУ коррелат (K.20):

N_{r r}*_r1 = W_r1. (K.67)

Вернёмся к вопросу получения элементов обратной матрицы с помощью некоторого алгоритма решения СЛАУ. Очевидно, что такой алгоритм будет линейным преобразованием свободных членов по некоторому правилу Z:

_r1 = N_{r r}^-1 W_{r 1} = Z_{r r} W_r1. (K.68)

Воспользовавшись тождеством N^-1 = N^-1 *I, выразим его через алгоритм Z:

^ = Z*I. (K.69)

Развернём этот результат подробнее:

. (K.70)

Из соотношений (K.70) следует очевидное правило вычисления столбцов обратной матрицы путём r-кратного использования алгоритма Z:

. (K.71)

5. МНК-оценивание

Коррелаты, полученные и проконтролированные на 4^ом этапе, позволяют вычислить МНК-поправки в измерения y_n1:

. (K.19)

Более подробно, с учётом (K.48), данная система записывается так:

. (K.72)

Получена коррелатная система уравнений поправок. Алгебраический эквивалент i-ой строки данной системы имеет вид:

. (K.73)

Вычисление МНК-поправок в измерения контролируется путём подстановки их в линеаризованные УУС (K.13):

B_{r n} = – W_r1. (K.74)

Допустимые значения МНК- поправок.

В статистических свойствах векторов-оценивателей коррелатной версии, установлено, что: E() = 0; а =KB^TN^-1BK. Из последнего факта следует, что , т.е. среднее квадратическое значение i-ой поправки – это диагональный элемент ковариационной матрицы МНК-поправок в измерения, находящийся на пересечении i-ой строки и i-ого столбца этой матрицы.

Установление допустимости поправки начинается с проверки нулевой гипотезы о равенстве нулю её МО:

H₀ = {E() = 0} (K.75)

против альтернативной гипотезы

H_A = {E() ≠ 0}. (K.76)

Нулевая гипотеза (K.75) проверяется с помощью теста

t_Э = | |/, (K.77)

который сопоставляется на уровне значимости α с квантилью t_T распределения Стьюдента, характеризующегося r = n – k степенями свободы:

t_T = arg(F_Ст.^(r)= (1–α/2)). (K.78)

Воспользовавшись неравенством альтернативной гипотезы (K.76), получаем такое выражение для допустимого значения МНК-поправки в i-ое измерение:

t_Э = | |/=t_T → ^доп = t_T* =t_T*. (K.79)

Квантиль распределения Стьюдента, как и ранее, может быть заменена квантилью нормального распределения на том же уровне значимости:

t_0.05 = 1.96 ≈ 2; t_0.01 = 2.58 ≈ 2.6; t_0.003 = 3. (K.58)

Если все невязки W_j были в допустимых пределах, то и МНК-поправки окажутся допустимыми. Тем не менее, наличие недопустимых невязок побуждает нас локализовать измерения, содержащие «промахи». В такой ситуации анализ МНК-поправок на допустимость может сыграть положительную роль.

6. МНК-оптимизация (уравнивание)

Данный этап является заключительным шагом процедуры уравнивания, выполняемой с целью нахождения НДЗ измерявшихся величин. С вычислительной точки зрения он элементарен:

.(K.23)

Каждое измерение получает соответствующую МНК-поправку:

.(K.80)

В качестве контроля необходимо проверить удовлетворение исходных УУС (K.3):

_{r 1}(; Z^T_1q) = 0_r1. (K.81)

Уравнения (K.81) должны быть удовлетворены с той точностью, с которой вычислялись невязки w_j.