13-03-2013_09-17-00 / 9_Неслучайные ошибки

В.А.Падве

ЛЕКЦИЯ: НЕСЛУЧАЙНЫЕ ОШИБКИ: ВЫЯВЛЕНИЕ И УЧЕТ.

1. Постановка вопроса.

Параметрическая и коррелатная версии классического алгоритма точностной оптимизации измерений по методу наименьших квадратов (МНК-оптимизация [1]) опираются, во-первых, на математические модели (ММ) измерений в виде параметрических (F) или условных (F) уравнений связи:

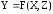
, (1)

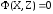
где Y - вектор истинных значений измеряемых величин;

X - вектор истинных значений параметров;

Z - вектор истинных значений опорных (исходных) координат.

Во-вторых, на их статистическое расширение:

а) априорную ковариационную матрицу измерений:

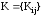, (2)

где K_ij - ковариации i-го и j-го измерений;

б) условие отсутствия систематических ошибок в измерениях, аналитическая запись которого имеет вид:

E(y) = Y или , (3)

где V = Y – E(y) - истинные случайные поправки к измерениям.

в) априорное значение масштабного показателя точности (МПТ) измерений полагается равным единице, т.е:

.

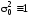Это следует из того факта, что

.

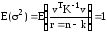После завершения процедуры МНК-оптимизации становятся известными МНК-поправки 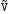в измерения y_n1:

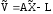(параметрическая версия)

, (4)

(коррелатная версия)

по которым вычисляется апостериорное значение МПТ

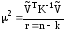, (5)

являющееся несмещенной оценкой его теоретического значения .

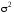Получив апостериорную оценку 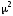, мы можем проверить гипотезу о равенстве истинного значения показателя его априорному значению 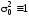против альтернативной гипотезы о неравенстве этих величин, т.е.

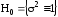(6)

против

.

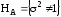Нулевая гипотеза проверяется с помощью теста "хи-квадрат":

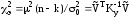, (7)

который сравнивается с двухсторонним ДИ, соответствующим уровню значимости a:

. (8)

"Нижняя" и "верхняя" границы этого ДИ представляют собой % и 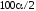% квантили распределения хи-квадрат[4]:

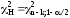, (9)

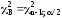. (10)

Если 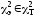, то H₀ не отвергается, т.е. исходные предположения (1)-(3) не противоречат результатам измерений и все материалы аттестуются как соответствующие заданным требованиям.

В противном случае, т.е. когда нулевая гипотеза отвергнута:

а) либо координаты опорных пунктов "Z" не могут рассматри­ваться в качестве безошибочных констант;

б) либо некорректно сформирована ковариационная матрица измерений K;

в) либо сами измерения y_n1 искажены неслучайными погрешностями, например, систематическими ошибками.

2. Анализ материалов и выявление неслучайных ошибок.

Для проверки предположения "а" необходимо обработать измерения повторно, не включая в ММ (1) величины "Z" полностью или частично и пользуясь, быть может, алгоритмом обработки "свободных сетей" [3]. Анализируя результаты обработки различных версий ММ (1), можно прийти к решению о том, какие из элементов вектора "Z" не могут рассматриваться как константы, и исключить их из ММ.

Когда не удается с помощью описанной процедуры идентифицировать "плохую" константу, то переходят к проверке других возможных источников отклонения нулевой гипотезы.

Некорректное формирование K (ковариационной матрицы измерений, предположение "б") происходит чаще всего из-за неправильно определенных априорных значений дисперсий измерений. Это предположение можно выдвинуть, анализируя графики зависимостей МНК-поправок в измерения от их порядковых номеров или каких-то других аргументов: длин ходов, числа станций, времени, продолжительности и т.п. Корректно определенные дисперсии дают картину зависимости МНК-поправок в виде равномерной полосы, шириной не более 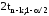, в идеале идущей вдоль оси аргументов (величина 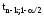представляет собой 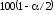% квантиль распределения Стьюдента). Неравномерность полосы, например ее расширение или сужение, как раз и свидетельствует о зависимости дисперсий от данного аргумента.

Последнее предположение "в" о наличии неслучайных ошибок в измерениях выдвигается, когда проверка двух первых не дала положительного эффекта. В такой ситуации можно воздействовать как на вектор параметров X, вплоть до введения такого вектора в коррелатную версию ММ, так и на сам оператор уравнений связи F или Ф. Указанное воздействие заключается в добавлении к одному, нескольким или всем измерениям дополнительных параметров или функций от них, моделирующих влияние предполагаемого систематического фактора.

Например, для параметрической ММ нивелирной сети, i-ое стандартное уравнение связи которой имеет вид h_i = x_j – x_m, где h_i – превышение между реперами с отметками x_j и x_m, i-ая строка матрицы линеаризованных уравнений связи A_nk запишется так:

1,2,….,j,.......,m,…..,k – № столбцов,

0 0…..1 0... -1 0.....0 – i-ая строка.

Заменив в этой ММ i-ое уравнение связи новым, описывающим предполагаемое воздействие постоянной ошибки "c" в простейшем виде, получим:

h_i = x_j – x_m +c (11)

Теперь i-ая строка матрицы линеаризованных уравнений связи A_n;k+1 преобразуется следующим образом:

1,2,…..,j,........,m,….,k,k+1 – № столбцов,

0 0...0 1 0….0 -1 0…..0 1 – i-ая строка.

По "расширенной" таким образом матрице A_n;k+1 выполняется вновь дальнейшая процедура обработки и анализа измерений, завершающаяся проверкой нулевой гипотезы (6) с помощью изменённого теста (7):

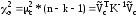, (12)

где 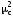– новая оценка МПТ, полученная по измененной ММ. Этот тест сравнивается с новым двухсторонним ДИ

, (13)

границы которого определяются квантилями

, (14)

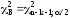. (15)

Если нулевая гипотеза (6) вновь отвергается, то модификация ММ продолжается до тех пор, пока тест (12) не попадет в ДИ (13). При этом рекомендуется внимательно изучать графики зависимости МНК-поправок, о которых выше шла речь, т.к. они не только отражают неправильность априорных значений дисперсий, но и, вообще, показывают, как происходит сглаживание результатов измерений для обсчитываемой в данном цикле модели.

3. Определение знàчимости систематических параметров.

После получения ММ, содержащей предполагаемые систематические параметры, необходимо проверить гипотезу о незнàчимости введенных параметров в совокупности:

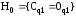. (16)

Практически этой гипотезе эквивалентна гипотеза (17) о равенстве дисперсий основной и модифицированной моделей:

. (17)

Если эта гипотеза будет отвергнута, то с целью упрощения ММ можно проверить гипотезы о незначимости каждого из новых параметров:

. (18)

Гипотеза (17) проверяется с использованием статистики Фишера [4]:

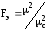, (19)

значение которой сопоставляется с квантилью F-распределения на уровне значимости "a":

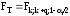. (20)

Она отвергается, когда F_Э > F_T.

Гипотеза (18) последовательно проверяется относительно каждого нового параметра с использованием t-теста [2]

, (21)

где 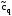- оценка параметра, а 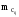- его СКО, определенная по материалам (ковариационной матрице параметров) МНК-оптимизации.

Тест (21) сопоставляется с 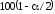% квантилью распределения Стьюдента:

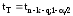. (22)

Гипотеза (18) отвергается, когда t_Э > t_T. Это означает, что параметр c_q знáчимо отличается от нуля и его следует сохранить.

Окончательный вариант ММ формируется последовательным прохождением всех описанных этапов таким образом, чтобы обязательно одновременно удовлетворялся тест (6) и модель содержала бы только те параметры c_q, которые не прошли тест (21). На основании этого можно будет утверждать на уровне значимости "a" о непротиворечивости построенной ММ результатам измерений. При этом необходимо четко представлять себе, что, например, оптимизированное превышение, описываемое уравнением связи (11) и занесенное в каталог, не будет равно простой разности оптимизированных отметок реперов, занесенных в этот же каталог, т.к. форма стандартного каталога не предусматривает наличие в нем информации о предполагаемых систематических параметрах.

Литература

1. М.М.Машимов

2. Ю.В.Линник

3. Ю.И.Маркузе

4. П.Мюллер, П.Нойман, Р.Шторм