13-03-2013_09-17-00 / 3_Матрицы и действия с ними

2. Матрицы и действия с ними

В данном разделе излагаются вопросы матричной алгебры в объёме, минимально необходимом для изложения теоретических вопросов, которые будут посвящены математической обработке систем измерений в геодезических построениях, обеспечивающих координатизацию пространства.

2. Определение матриц

Матрица представляет собой массив чисел или буквенных обозначений, упорядоченных в форме прямоугольной таблицы, состоящей из «m» строк и «n» столбцов, которые записываются в виде нижних индексов при имени матрицы:

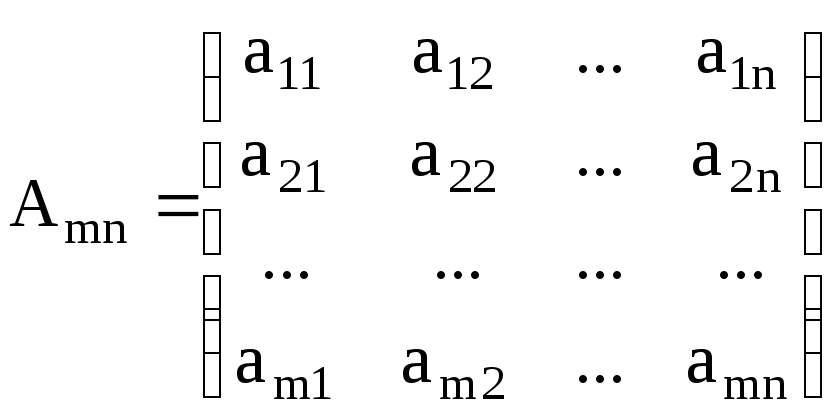. (M.1)

Матрица может содержать только одну строку или один столбец. Это будет матрица-строка или матрица-столбец. Часто их называют вектор-строка или вектор-столбец соответственно:

, (M.2)

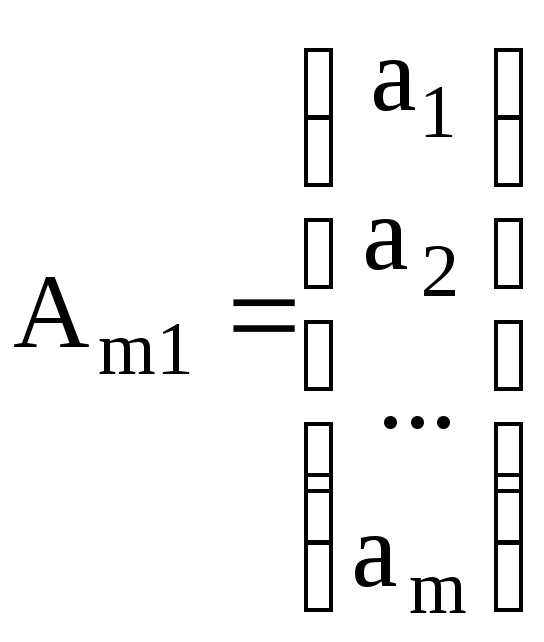. (M.3)

Когда число строк равно числу столбцов, матрица становится квадратной:

. (M.4)

Квадратные матрицы, в свою очередь бывают:

а) диагональными

= diag{a₁₁, a₂₂,…,a_nn}; (M.5)

б) верхними треугольными

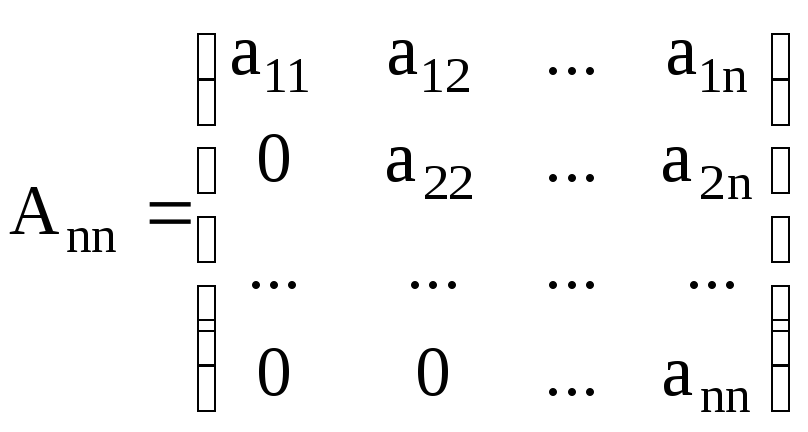; (M.6)

в) нижними треугольными

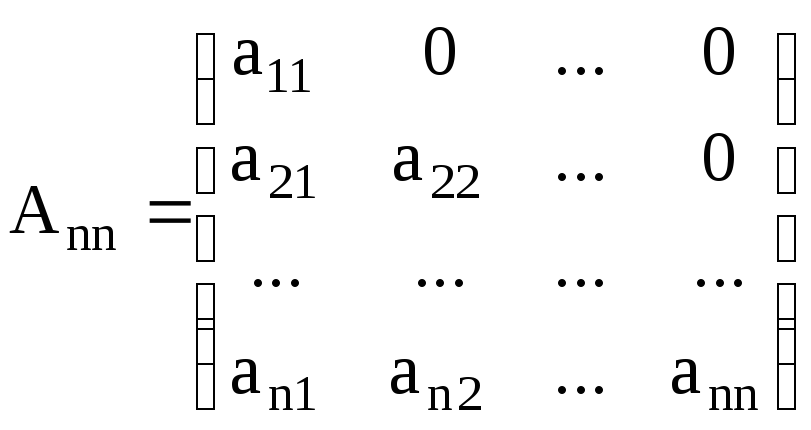. (M.7)

Среди диагональных матриц особое место занимает единичная матрица, каждый диагональный элемент которой равен единице:

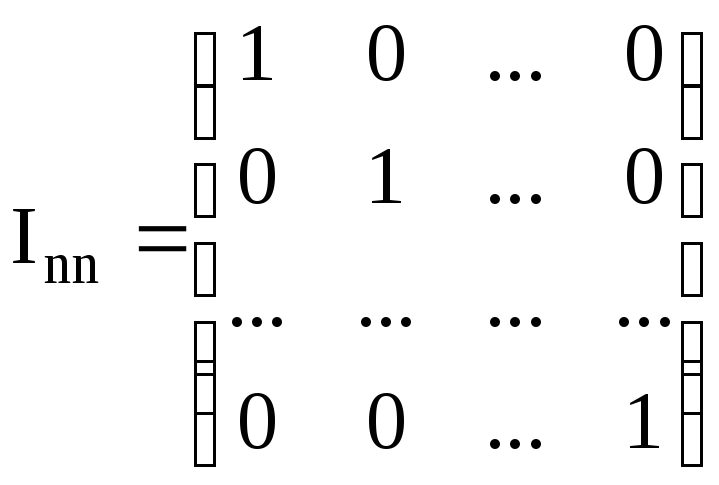. (M.8)

Любая матрица, все элементы которой равны нулю, называется нулевой матрицей: 0_mn. В частности, это может быть нулевая строка – 0_1n или нулевой столбец – 0_m1.

Две матрицы A_mn и B_pq называются подобными, если они имеют одинаковое количество строк и столбцов, т.е. если m = p, а n = q одновременно.

Две матрицы A_mn и B_pq равны, т.е. A_mn = B_pq , если, во-первых, они подобны и, во-вторых, a_ij = b_ij ,i, j, т.е . каждый элемент матрицы A_mn равен соответствующему элементу матрицы B_pq. Равенство подразумевает:

1) рефлексивность – (A = A);

2) симметричность – (из равенства A = B следует B = A);

3) транзитивность – (из равенств A = B и B = C следует, что A = C).

2. Операции над матрицами

Матрицы являются алгебраическими объектами, допускающими над собой определённые операции. Рассмотрим некоторые из этих операций.

1. Сложение матриц

Складываются только подобные матрицы A_mn и B_mn. Сложение выполняется поэлементно, т.е. для матрицы-суммы C = A + B каждый из её элементов находится по формуле c_ij = a_ij + b_ij.

Свойства операции сложения:

1. A + B = B + A;

2. A + B + C = (A + B) + C = A + (B + C) = (A + C) +B;

3. A + 0 = A.

2. Умножение матрицы на скаляр

Умножение матрицы A_mn на скаляр «α» подразумевает, что каждый элемент a_ij умножается на этот скаляр:

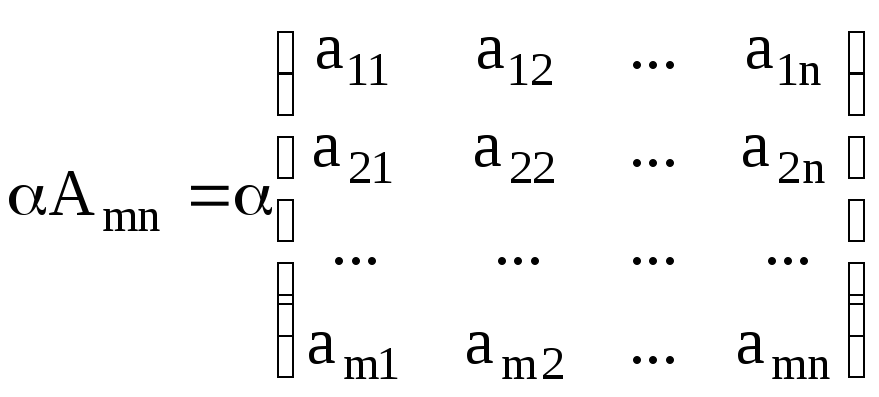
(M.9)

Свойства операции умножения матрицы на скаляр:

1. αA = Aα;

2. α(A + B) = αA + αB.

3. Умножение матриц

Запись C_mq = A_mnB_pq означает, что матрица C_mq представляет собой произведение матриц A_mn и B_pq когда число столбцов «n» левого сомножителя равно числу строк «p» правого сомножителя. Каждый элемент c_ij матрицы-произведения C_mq представляет собой скалярное произведение i-го вектора-строки матрицы A_mn на j-ый вектор-столбец матрицы B_pq:

c_ij = a_i1b_1j + a_i2b_2j +…+ a_inb_pj =. (M.10)

Свойства операции умножения матриц:

1. A_mnB_pq ≠ B_pqA_mn; правое произведение может не существовать по определению, но даже если q = m матрица B_pqA_mn, во-первых, может не оказаться подобной и, во-вторых, будет состоять из произведений других строк и столбцов;

2. αAB = AαB = ABα;

3. A(B + C) = AB + AC;

4. (A + B)(C + D) = AC + AD + BC + BD;

5. A*I = I*A = A; 6) A*0 = 0.

4. Транспонирование матриц

Операция транспонирования осуществляет взаимную замену строк и столбцов, имеющих одинаковые номера. Будем обозначать операцию транспонирования литерой T в виде верхнего правого индекса. Нижние индексы, обозначающие число строк и столбцов транспонированной матрицы, будем менять местами:

исходная матрица

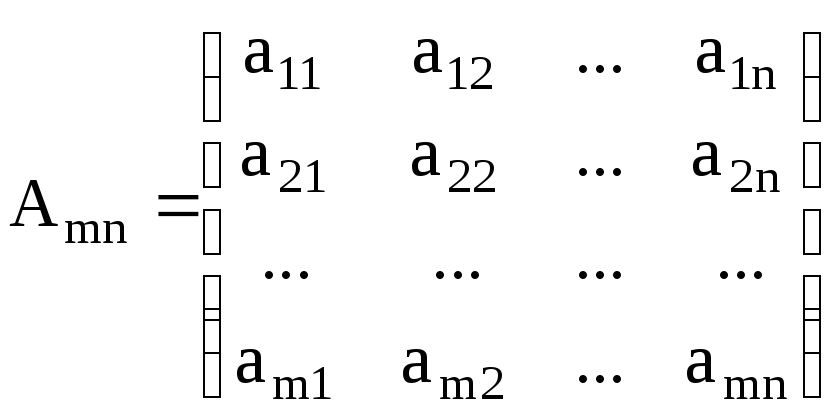, (M.1)

транспонированная матрица

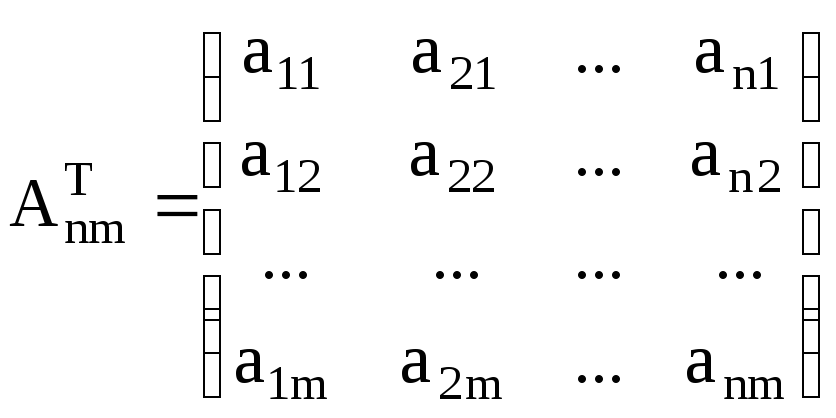. (M.11)

Свойства операции транспонирования матриц:

1. (A^T)^T = A;

2. (A_mnB_pq)^T = B_qp^TA_nm^T при условии, что n = p;

3. (αA)^T = αA^T;

4. (A + B)^T = A^T + B^T.

Существуют квадратные матрицы, у которых каждая i-ая строка идентична соответствующему i-му столбцу. Такие матрицы называются симметрическими. Симметрические матрицы не реагируют на транспонирование, т.е. A^T = A и, как следствие, a_ij = a_ji.

5. Обращение квадратных матриц

Матрица A_nn^-1 называется обратной по отношению к некоторой исходной квадратной матрице A_nn, если, будучи умноженной, слева или справа, на эту исходную, она даёт единичную матрицу такого же размера:

A^-1*A = A*A^-1 = I. (M.12)

Свойства операции обращения квадратных матриц:

1. (A^-1)^-1 = A;

2. (A^-1)^T = (A^T)^-1;

3. (AB)^-1 = B^-1A^-1;

4. (αA)^-1 = 1/α*A^-1;

5. (A + B)^-1 ≠ A^-1 + B^-1.

Матрица, обратная квадратной, строится следующим образом.

1. вычисляется определитель исходной матрицы – det(A). Если det(A) ≠ 0, то A^-1 существует, а матрица A является неособенной;

2. строится союзная к A матрица, состоящая из алгебраических дополнений A_ij = (–1)^i+jM_ij, представляющих собой соответствующие миноры M_ij матрицы A, знак перед которыми определяется знаком величины (–1)^i+j; каждое алгебраическое дополнение A_ij записывается в союзную матрицу на пересечении j-ой строки с i-ым столбцом;

3. все элементы союзной матрицы делятся на определитель такой неособенной матрицы det(A).

На этом процедура получения обратной матрицы завершается.

Проиллюстрируем вышеизложенное на примере построения обратной матрицы для неособенной матрицы второго порядка

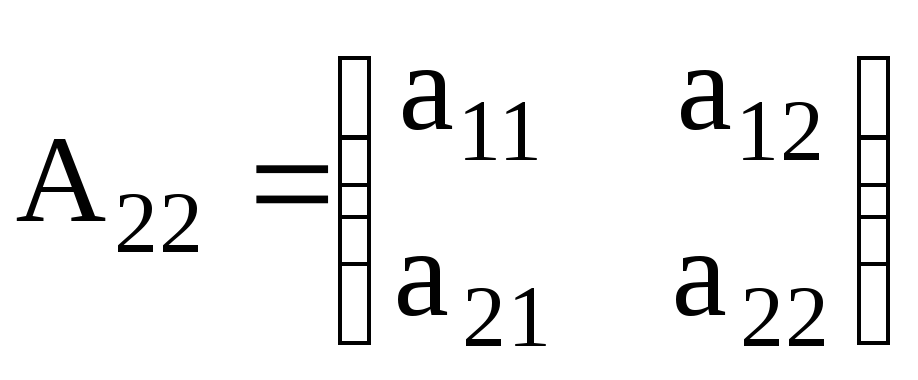. (M.13)

Найдём определитель этой матрицы:

det(A) = Δ = a₁₁*a₂₂ – a₁₂*a₂₁≠ 0. (M.14)

Далее получим алгебраические дополнения:

A₁₁ = (–1)¹⁺¹*a₂₂; A₁₂ = (–1)¹⁺²*a₂₁; A₂₁ = (–1)²⁺¹*a₁₂; A₂₂ = (–1)²⁺²*a₁₁.

Теперь сгруппируем алгебраические дополнения в союзную матрицу, разделив их на определитель Δ, и получим матрицу A^-1, обратную к исходной A:

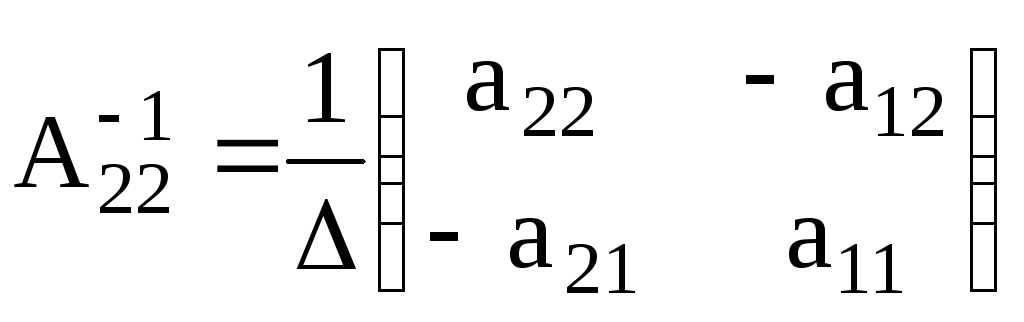(M.15)

Разобранный выше теоретически корректный путь построения обратной матрицы на практике далее матриц второго порядка не применяется. Можно найти элементы обратной матрицы с использованием разнообразных алгоритмов решения систем линейных алгебраических уравнений (СЛАУ), с которыми мы познакомимся позже.

6. След квадратной матрицы и его свойства

Квадратная матрица А_nn характеризуется «следом», равным сумме её диагональных элементов: tr(A_nn) = åа_ii.

Оператор следа tr(…) обладает следующими свойствами:

1) tr(a) = a, где a – скаляр; 2) tr(a*А) = a*trА; 3) tr(А+В) = trА + trВ;

4) tr(А_{m n}*В_{n m}) = tr(В_{n m}*А_{m n}); 5) E(tr(А)) = tr(E(А)).

7. Дифференцирование функций векторного аргумента

Функция «z», зависящая от «n» переменных x_i, может быть представлена как функция векторного аргумента:

z = f(x₁, x₂, … x_n) = f(X_1n^T). (M.16)

Частные производные такой функции удобно записать в виде вектора-строки:

∂z/∂X = (∂f/∂x₁ ∂f/∂x₂ … ∂f/∂x_n). (M.17)

Символ ∂/∂X, использованный в формуле (M.17), называется вектором дифференциальных операторов [8].

Используя оператор (M.17), найдём в n-мерном пространстве вектор частных производных гиперплоскости

z = C_1n*X_n1 (M.18)

и гиперповерхности второго порядка, называемой в математике квадратичной формой:

z = . (M.19)

Матрица C_nn предполагается симметрической, т.е. .

Следующая последовательность преобразований с применением вектора дифференциальных операторов (M.17) доказывает, что вектор частных производных гиперплоскости (M.18) – это вектор её коэффициентов C_1n:

∂z/∂X=. (M.20)

Итак, ∂( C_1nX_n1)/∂X = C_1n.

Далее построим вектор частных производных для квадратичной формы, преобразовав предварительно уравнение (M.19) к обычной алгебраической форме;

z = =(x₁ x₂ … x_n)*=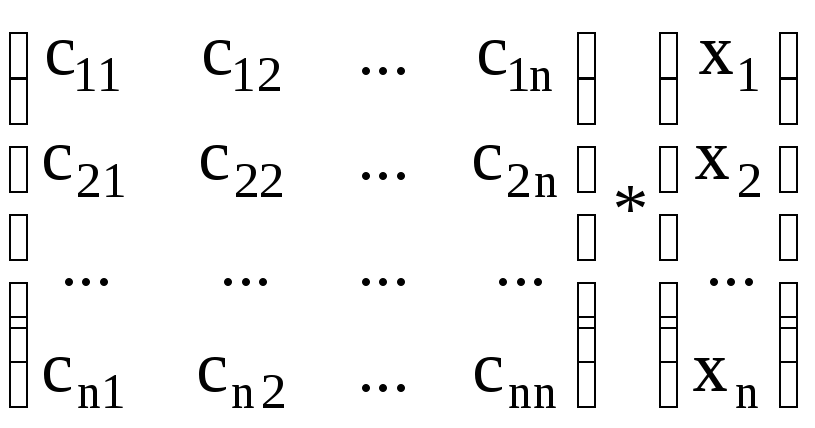

=(c₁₁x₁² + c₁₂x₁x₂ + … + c_1nx₁x_n +

+ c₂₁x₂x₁ + c₂₂x₂₂² + … + c_2nx₂x_n +

… … … … …

+ c_n1x_nx₁ + c_n2x_nx₂+ … + c_nnx_nn²). (M.21)

Теперь квадратичная форма (M.19) готова к дифференцированию по классическим правилам:

∂z/∂X=

=. (M.22)

Окончательно, ∂(X_1n^T*C_1n*X_n1)/∂X = 2 X_1n^T*C_1n .

2. Запись и решение СЛАУ с помощью матриц

Матрицы позволяют вести очень компактную запись систем линейных алгебраических уравнений (СЛАУ). Обратимся к СЛАУ, представленной в алгебраической форме:

b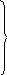₁₁v₁ + b₁₂v₂ + … +b_1nv_n + w₁ = 0

b₂₁v₁ + b₂₂v₂ + … +b_2nv_n + w₂ = 0

… … … … . (M.23)

… … … …

b_r1v₁ + b_r2v₂ + … +b_rnv_n + w_r = 0

Введём прямоугольную матрицу коэффициентов этих уравнений

, (M.24)

матрицу-столбец (вектор-столбец) неизвестных

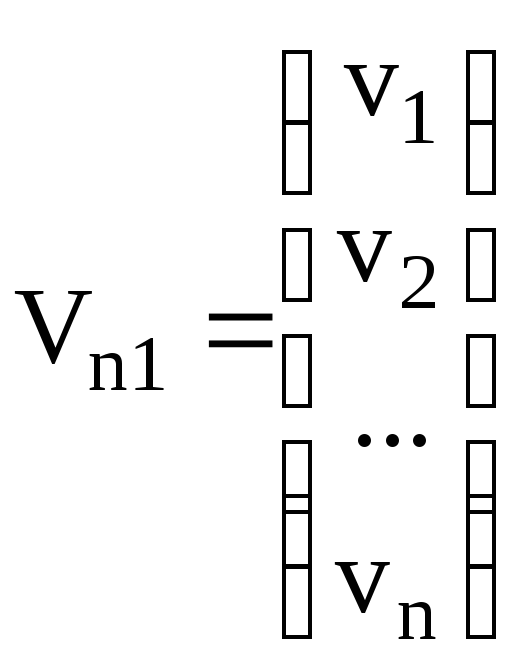, (M.25)

вектор-столбец свободных членов

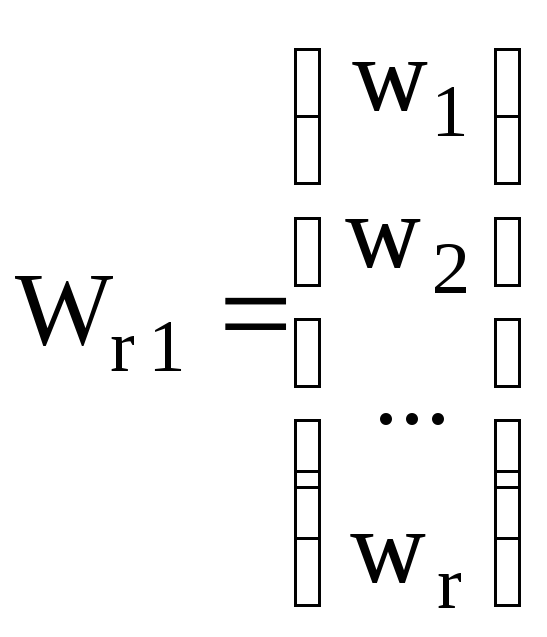(M.26)

и нулевой вектор-столбец правой части системы (M.23)

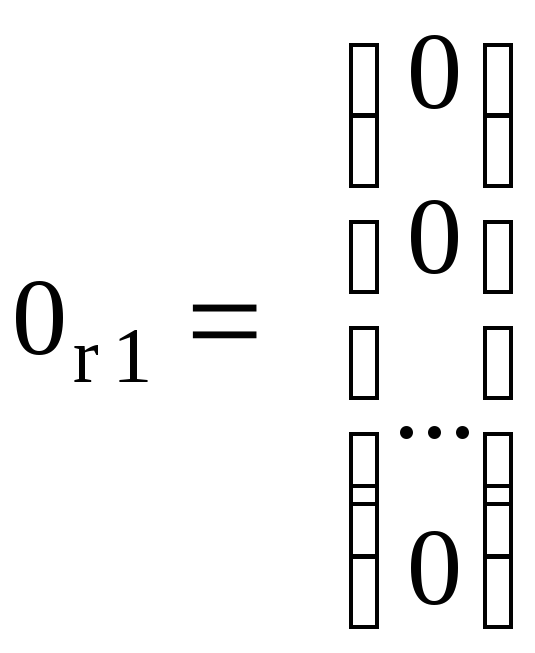. (M.27)

В соответствие с операциями над матрицами, изложенными в предыдущем разделе, мы можем записать матричный эквивалент системы (M.23) кратко

B_{r n} * V_{n 1} + W_{r 1} = 0_{r 1} (M.28)

или развёрнуто

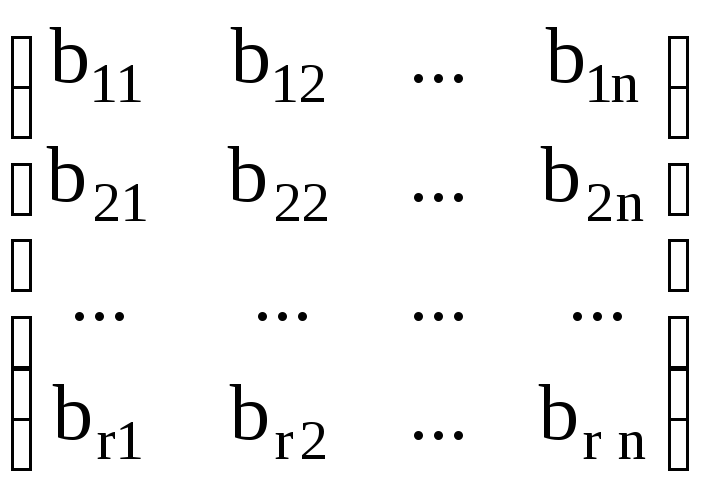*+=. (M.29)

Когда в СЛАУ число уравнений равно числу неизвестных, то матрица коэффициентов становится квадратной. Если определитель такой матрицы не равен нулю, то матрица её коэффициентов будет неособенной. В таком случае существует обратная к ней матрица, с помощью которой просто записывается решение системы.

Пусть СЛАУ

A_{n n} * X_{n 1} = b_{n 1}. (M.30)

характеризуется неособенной матрицей коэффициентов (detA ≠ 0), а ранг расширенной матрицы (A_nnb_n1) равен рангу матрицы коэффициентов, т.е. rank(A) = rank(Ab). Такая система называется совместной.

Умножив систему (M.30) слева на обратную матрицу A_nn^-1, мы получим решение данной СЛАУ в виде вектора неизвестных:

X_{n 1} = A_nn^-1*b_{n 1}. (M.31)