3. Нормализация

Нормальные параметрические уравнения имеют вид:

. (П.13)

Коэффициенты нормальных уравнений представляют собой тройное произведение двух ранее введённых матриц:

N_kk = A_nk^T K_nn^-1A_nk, (П.14)

а свободные члены равны произведению трёх матриц:

G_k1 = A_nk^T K_nn^-1L_n1. (П.15)

Выполнив умножение данных матриц с учётом (П.45) и (П.46), получим алгебраическую запись коэффициентов и свободных членов нормальных параметрических уравнений для случая некоррелированных измерений:

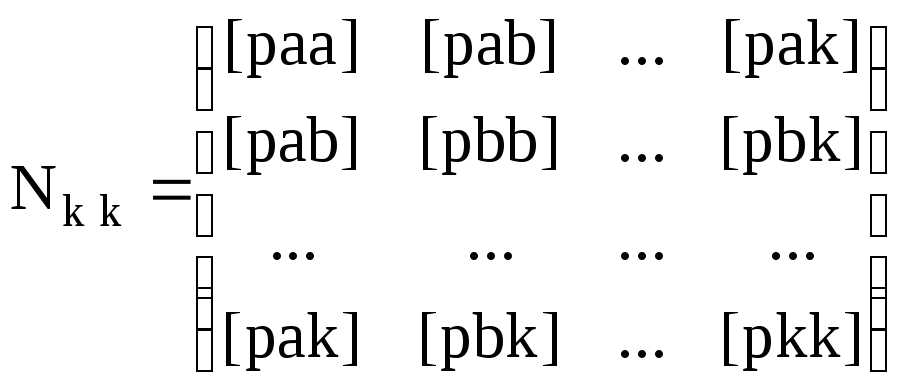, (П.51)

(П.52)

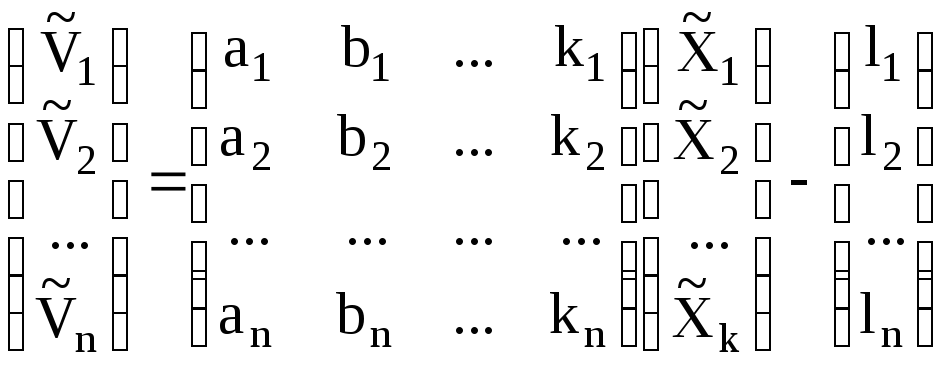
Вектор неизвестных (МНК-поправок к параметрам), записанный в строку, имеет вид:

(П.53)

Теперь, выполнив умножение матрицы (П.51) на вектор неизвестных (П.53) и вычтя из произведения вектор свободных членов (П.52), получим алгебраическую запись системы параметрических НУ:

. (П.54)

4. Решение ну

Решение параметрических НУ, предлагаемое в теоретической части изложения материала, осуществляется методом обращения матрицы коэффициентов N_{k k} системы параметрических НУ (П.13):

. (П.17)

Это возможно, если компоненты вектора X_k1 линейно независимы. Следствием такой независимости будет тот факт, что матрица коэффициентов A_nk – это матрица полного столбцового ранга, т.е. rank(A) = k. В таком случае матрица коэффициентов параметрических НУ N_{k rk} = A_{k n}^TK^-1A_{n k} будет иметь такой же ранг, и её определитель не будет равен нулю, т.е. det(N_{k k}) ≠ 0. Это означает, что существует N^-1 и решение системы (П.54) в форме (П.17).

В развёрнутом виде уравнения (П.17) можно записать, учитывая тот факт, что обратная матрица коэффициентов нормальных уравнений является ковариационной матрицей её корней, т.е. N_{k k}^-1 = :

. (П.55)

Каждый диагональный элемент K_jj – это квадрат средней квадратической ошибки j-ой поправки к своему параметру.

Отдельно j-ая строка системы (П.55) выглядит следующим образом:

_j = K_{j 1}* [pal] + … +K_{j j}*[pjl] + … + K_{j k}*[pkl]. (П.56)

Естественно, что параметрические НУ могут, как и коррелатные, быть решены любым другим способом.

МНК-поправки к параметрам вычисленные методом обращения или методом Гаусса, либо каким-то другим способом, должны быть проконтролированы. Такой контроль осуществляется путём подстановки найденных корней в исходную систему параметрических НУ (П.13):

N_kk*_k1 = G_k1. (П.57)

5. МНК-оценивание

Найденные МНК-поправки к параметрам x_k1, проконтролированные на 4^ом этапе, позволяют вычислить МНК-поправки в измерения y_n1:

= A_nk * –L_n1. (П.10)

Более подробно система (П.10) записывается так:

. (П.58)

Получена параметрическая система уравнений поправок. Алгебраический эквивалент i-ой строки данной системы имеет вид:

. (П.59)

Вычисление МНК-поправок в измерения контролируется путём использования леммы Гаусса:

. (П.12)

Допустимые значения МНК- поправок.

В статистических свойствах векторов-оценивателей параметрической версии, установлено, что: E() = 0; а =K–AN^-1A^T. Из последнего факта следует, что , т.е. среднее квадратическое значение i-ой поправки – это диагональный элемент ковариационной матрицы МНК-поправок в измерения, находящийся на пересечении i-ой строки и i-ого столбца этой матрицы.

Установление допустимости поправки начинается с проверки нулевой гипотезы о равенстве нулю её МО:

H₀ = {E() = 0} (П.60)

против альтернативной гипотезы

H_A = {E() ≠ 0}. (П.61)

Нулевая гипотеза (П.60) проверяется с помощью теста

t_Э = | |/, (П.62)

который сопоставляется на уровне значимости α с квантилью t_T распределения Стьюдента, характеризующегося n – k степенями свободы:

t_T = arg(F_Ст.^(n-k)= (1–α/2)). (П.63)

Воспользовавшись неравенством альтернативной гипотезы (П.61), получаем такое выражение для допустимого значения МНК-поправки в i-ое измерение:

t_Э = | |/=t_T → ^доп = t_T* =t_T*. (K.79)

Квантиль распределения Стьюдента может быть заменена квантилью нормального распределения на том же уровне значимости:

t_0.05 = 1.96 ≈ 2; t_0.01 = 2.58 ≈ 2.6; t_0.003 = 3. (П.80)

Данный контроль позволяет нам локализовать измерения, содержащие «промахи» и может сыграть положительную роль в анализе качества измерений.

6. МНК-оптимизация (уравнивание)

Данный этап является заключительным шагом процедуры уравнивания, выполняемой с целью нахождения НДЗ измерявшихся величин и приближённых значений параметров. С вычислительной точки зрения он элементарен:

= x_k1 + , (П.18)

.(П.19)

Каждый параметр и каждое измерение получают соответствующие МНК-поправки:

(П.81)

.(П.82)

В качестве контроля необходимо сверить уравненные значения измерений, вычисленные по формуле (П.19), со значениями этих же величин, полученными по исходным ПУС (П.1):

= F_n1(;Z^T_1q). (П.83)

Уравнения (П.83) должны быть удовлетворены с той точностью, с которой вычислялись свободные члены L_n1.

Выполнение контроля (П.83) зависит от степени близости приближенных значений параметров x_k1 к их истинным значениям X_k1. Электронные пакеты прикладных геодезических программ обеспечивают близость, эквивалентную близости результатов измерений y_n1 к истинным значениям измеряемых величин Y_n1. При ручной обработке данных приближённые значения параметров x_k1 могут оказаться «грубыми» и разложение исходных ПУС пройдёт «не гладко». В таком случае потребуются итерации, в которых за новые приближённые значения параметров принимают их только что уравненные значения:

(x_k1)^нов = . (П.84)

После этого вновь повторяются все шесть первых этапов, и проверяется контроль (П.83). Если контроль удовлетворён, то МНК-оптимизация (уравнивание) завершается. При очень грубых начальных значениях параметров процесс итерации может оказаться расходящимся.