3.2. Принцип соответствия между классической и квантовой физикой

Важно подчеркнуть, что теория Бора является не только теорией атома водорода, но и теорией взаимодействия электромагнитного излучения с атомом, т.к. важные черты этого взаимодействия описываются 2-м и 3-м постулатами Бора. Дальнейшее развитие теории взаимодействия излучения с атомами может быть осуществлено не прибегая к последовательному квантово-электродинамическому формализму, а используя так называемый принцип соответствия в духе полуклассического подхода Бора. Отправной точкой такого рассмотрения является выражение для мощности дипольного излучения, известное из классической электродинамики. Оно имеет вид

, (3.22)

где

(3.23)

– дипольный момент частицы с зарядом под которой в дальнейшем будем понимать электрон. Две точки над символом дипольного момента в формуле (3.22) обозначают вторую производную по времени. Критерий применимости дипольного приближения, в рамках которого получена формула (3.22), может быть сформулирован в виде неравенства

, (3.24)

где а – размер области пространства, ответственной за излучение, – длина волны излучения. В случае атома, когда, условие (3.24) охватывает широкий диапазон длин волн вплоть до жесткого рентгеновского излучения.

Вторая производная по времени от дипольного момента, фигурирующая в правой части равенства (3.22), элементарно выражается через ускорение электрона :. С учетом этого формула (3.22) перепишется в виде [1]:

(3.25)

Таким образом, в рамках классической физики ускоренно движущаяся заряженная частица будет терять свою энергию на дипольное излучение со скоростью, определяемой формулой (3.25). Заметим, что потеря энергии зарядом, находящимся в кулоновском поле, приводит не к уменьшению, а к увеличению его кинетической энергии. Это видно и из квантовых формул (3.10) – (3.12). Увеличение кинетической энергии заряда сопровождается в два раза большим уменьшением его потенциальной энергии (см. формулу (3.13)), что связано с уменьшением расстояния до центра кулоновского поля. В результате полная энергия электрона уменьшается.

В случае периодического движения заряда с круговой частотой , как это имеет место с атомным электроном, представляет интерес мощность излучения, усредненная по периоду движения. Для того чтобы произвести это усреднение в формуле (3.22), воспользуемся следующим равенством, справедливым для действительной периодической функции:

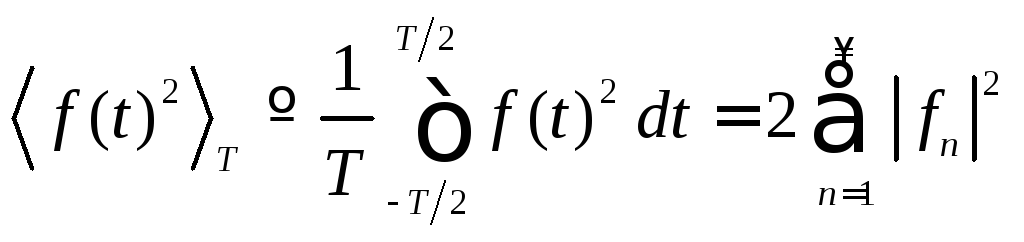, (3.26)

где

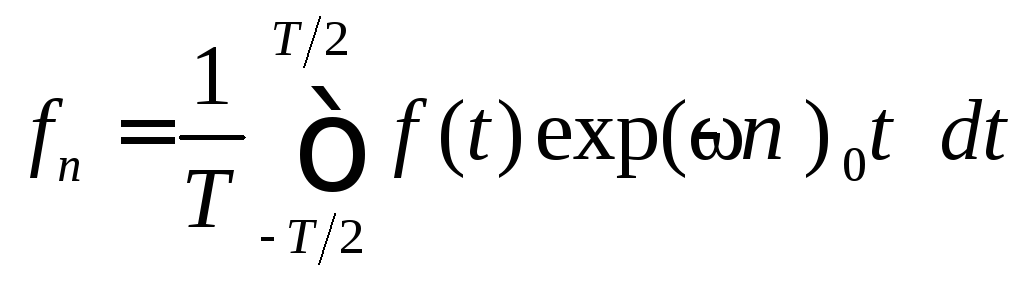(3.27)

– n-я гармоника разложения в ряд Фурье функции . При выводе формулы (3.26) было предположено, что среднее по периоду от рассматриваемой функции равно нулю, т.е.. Заметим, что коэффициент 2 в правой части равенства (3.26) связан с учетом вклада отрицательных гармоник ряда Фурье ().

Пользуясь равенством (3.26), в котором положено, для усредненной по периоду мощности дипольного излучения получаем из (3.22) следующее выражение:

, (3.28)

где

. (3.29)

С учетом того, что

(3.30)

из формулы (3.29) находим

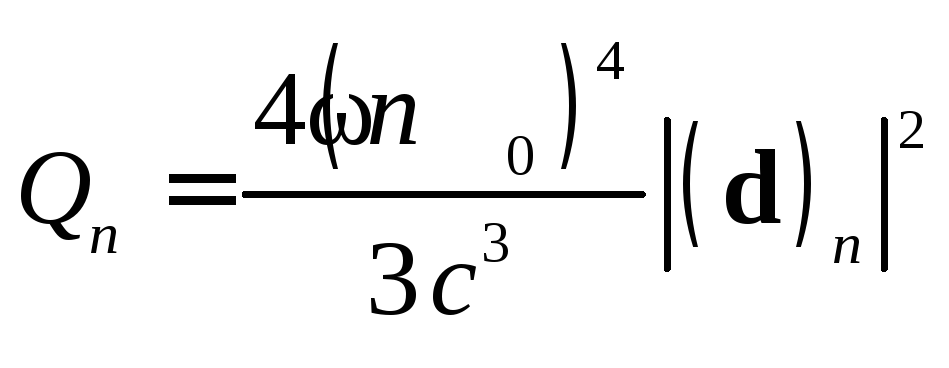. (3.31)

Формула (3.31) описывает мощность дипольного излучения на частоте n-й гармоники . В частности, мощность излучения на частоте периодического движения электрона(n = 1) равна

. (3.32)

Здесь мы переобозначили 1-ю фурье-гармонику дипольного момента: .

Заменим теперь в формуле (3.32) фурье-гармонику дипольного момента на его матричный элемент, вычисленный между состояниями и(– волновые функции этих состояний):

, (3.33)

а частоту периодического движения на частоту перехода:

. (3.34)

В результате вместо формулы (3.32) получим

. (3.35)

Величина (3.35) может быть названа мощностью электромагнитного излучения при переходе атомного электрона из стационарного состояния в стационарное состояние. Она описывает интенсивность излучения различных спектральных серий атома водорода: Лаймана (m = 1), Бальмера (m = 2), Пашена (m = 3) и т. д. Надо, однако, иметь в виду, что, в отличие от классической мощности излучения (3.22), величину (3.35) нужно понимать в статистическом смысле, т.е. как результат усреднения по ансамблю атомов.

Если теперь мощность излучения (3.35) разделить на энергию рассматриваемого перехода , то получим величину, имеющую размерность обратного времени, которая совпадает с коэффициентом Эйнштейна для спонтанного излучения:

. (3.36)

В последнем равенстве формулы (3.36) введено время жизни состоянияпо отношению к его спонтанному распаду с переходом в нижележащее состояние. Это время для переходав атоме водорода равно:.

Таким образом, использование формулы классической электродинамики (3.22) и замен (3.33)–(3.34) позволили получить квантовый результат для мощности излучения спектральных линий (3.35) и вероятности спонтанного излучения (3.36). Это обстоятельство является отражением принципа соответствия между классической и квантовой физикой. Данный принцип может быть сформулирован следующим образом. Квантово-механические выражения получаются из классических, если в последних фурье-компоненты физических величин заменить на матричные элементы этих величин. Причем частота квантового перехода должна совпадать с частотой фурье-компоненты.

Любопытно отметить, что наличие конечного времени жизни возбужденного состояния может быть интерпретировано в духе принципа соответствия, как «падение» электрона на ядро за счет излучения фотонов – тот самый процесс, против которого «борется» второй постулат Бора. Это «падение» продолжается до тех пор, пока электрон не достигнет основного состояния, обладающего наименьшей возможной с точки зрения квантовой физики энергией.

Чтобы выяснить физическое обоснование 2-го постулата Бора, введем классический период вращения электрона на -орбите:

. (3.37)

При записи формулы (3.37) были использованы выражения (3.6), (3.7) и (3.9). Оценим теперь отношение периода (3.37) ко времени жизни . Пользуясь (3.36)–(3.37) и полагая, что, где– некоторая функция порядка и меньше единицы, приближенно имеем

, (3.38)

где для больших номеров(см. асимптотическую формулу в таблице 1). Второе приближенное равенство в (3.38) отражает тот факт, что время жизни возбужденного состояния атома водорода определяется его переходом в основное состояние.

Из полученного соотношения (3.38) следует, что период обращения электрона по классической орбите на несколько порядков величины меньше времени жизни в данном состоянии . Таким образом, эти состояния с хорошей степенью точности можно считать стационарными в соответствии с первыми двумя постулатами Бора. Эта стационарность есть следствие малой величины постоянной тонкой структуры, ответственной за электромагнитное взаимодействие.