31.Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена.
1.Ряд
Тейлора
– Если функция f(x)
имеет производные любых порядков в
окрестности точки
,
то можно записать разложений функцийf(x)
по степеням (
):
(1)
(1) – называется рядом Тейлора.
Если
в формуле (1) положить
,
то получим разложение по степенямx,
которая называется рядом
Маклорена,
т.е.:
(2)
Формулу
(1) можно записать в виде:
,
где
,
-
многочлен
Тейлора,
,
,
-
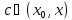остаточный член ряда Тейлора, записанный
в форме Лагранжа. (3)
Ряд
Тейлора можно формально записать для
любой бесконечно дифференцируемой
функции в окрестности точки
,
однако он может быть расходящимся или
сходится, но не к функцииf(x).
Теорема:
Для того чтобы ряд Тейлора (1) функции
f(x)
сходится к функции f(x)
в точке x
необходимо и достаточно, чтобы в этой
точке остаточный член
формула (3) стремился к нулю при
.
(4)
Задача
разложения функции f(x)
в степенной ряд сводится к определению
значений x,
при которых
стремится к нулю. Если это сделать
непросто, то следует использовать другой
способ, например применить признак
Даламбера и Коши.
2.Разложение некоторых элементарных функций в ряд Маклорена – для разложение функции f(x) в ряд Маклорена (2) надо:
1.Найти
производные f
(x),
f
(x)
и т.д. fn(x);
2.Вычислить
их значение в точке
;
3.Подставить в ряд (2);
4.Найти интервал сходимости ряда ли найти интервал (-R,R), в котором остаточный член ряда стремится к нулю. Эти интервалы совпадают;
Таблица основных разложений элементарных функций в ряд Маклорена:
1.
,
;
2.
,
;
3.
,
;
4.
,
;
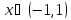5.
,
;
6.
,
;
7.
,
;
32.Разложение в ряд Маклорена функций еx , sin X.
:
1.Находим
производные:
;
;
…………….
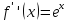2.Вычислим
значение функции в 0:
;
;
;
……………
;
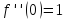3.Подставляем
в ряд Маклорена:
;
4.Находим
радиус сходимости:
;
Интервал
сходимости
.
:
1.
;
;
;
;
…………………………………..
;
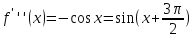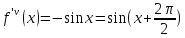2.
;
;
;
;
;
……………
;
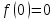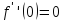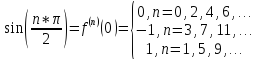3.
;
4.
;
Интервал
.
33.Приложение степенных рядов. Приближенное вычисление значений функций. Вычислить sin1 с точностью δ= 10-3.
Приближенное
значение вычисление значений функции:
Пусть требуется вычислить значение
функции f(x),
при
,
с заданной точностью
.
Если функциюf(x)
в интервале (-R,R)
можно разложить в степенной ряд:
и
,
т.е.
,
то точное значение
сумме
этого ряда, а приближенное значение
равно частичной сумме этого ряда
.
Точность этого равенства увеличивается
с ростомn.
Абсолютная погрешность этого равенства
равна:
,
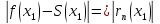где
- остаток ряда. Таким образом, оценив
остаток можно найти ошибку. А для
знакочередующего ряда:
.
Вычислить sin1 с точностью δ= 10-3:
;
.
Этот ряд сходится по признаку Лейбница.
Сравним
каждый ряд с
:
:
;
:
;
:
;-
этот в сумму не включается.
.
На
калькуляторе
.
34.Приложение
степенных рядов. Приближенное вычисление
интегралов. Вычислить интеграл
с точностью δ= 10-3.
Приближенное вычисление интегралов: В теории вероятностей большое значение имеет интегральная функция Лапласса:
Для нее составлены таблицы значений.
Вычислим значение функции Лапласса с помощью разложения в ряд подинтегральной функции при x = 0,5, с точностью δ= 10-3 и сравним с табличным.
-
не берущийся. Воспользуемся разложением
функции
:
.
Заменим
x
на (
):
:
;
:
;
:
;
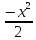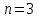- не включаем.
.
Из
таблицы
.