БТЖ и ФРГП на весну 16 года / БТЖ - лекции_2015 / СулакшинЧубик

лы будет определяться сопротивлением породы смятию-скалыванию (или сдвигу) σСК и величиной площади скалывания элемента породы SСК, зависящей от угла скалывания γСК породы:

Таким образом, при внедрении резца в породу под действием нагрузки G0 резец перемещается в двух направлениях под действием сил G1 и G2 (см. рис. 3.38, в): вертикальном и горизонтальном, вследствие того, что σСК<РВ, а задняя грань резца наклонна. В процессе такого движения резца и возникают силы N1 и N2, а также силы трения на передней ТПГ и задней ТЗГ гранях (см. рис. 3.42).

Величина сил трения определяется силой прижатия граней резца к породе (N1, N2) и величиной коэффициента трения f пары твёрдый сплав–порода:

где ϕи − угол трения ПРЭ о породу.

Таким образом, условием внедрения резца в породу является превышение силы нагружения резца G0 суммы сил сопротивления его внедрению:

За критерий эффективности РГП в этом случае принимают глубину внедрения резца h при определённой величине нагрузки G0. С целью определения h − показателя эффективности РГП – прибегают к следующим вычислениям.

Составляется уравнение действующих на резец сил в проекции их на горизонтальную плоскость (см. рис. 3.42):

Заменив силу трения ТЗГ её значением (3.83), имеем:

Произведя преобразования, находим значение N1:

151

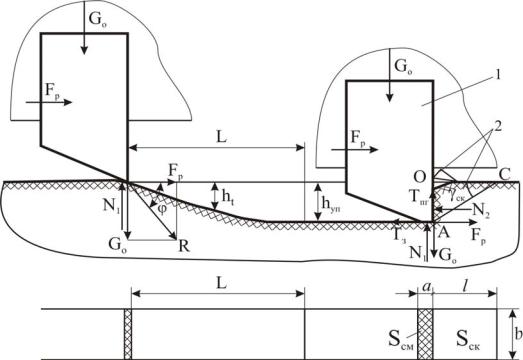
Рис. 3.43. Схемы разрушения породы твёрдосплавным резцом при внедрении под действием осевой нагрузки G0 и перемещении вдоль плоскости резания под действием силы резания FР:

1 – резец; 2 – элементы скалываемой породы

тается установившимся при условии равенства всех активных и реактивных сил, действующих на резец.

Однако практически при очень нестабильных динамических условиях работы коронки в забое процесс разрушения горной породы происходит с изменяющейся глубиной внедрения резца и, соответственно, толщиной снимаемого слоя h.

Таким образом, процесс РГП при вращении ПРИ с резцами из твердых сплавов в общем случае сводится к внедрению резцов на некоторую глубину hУП под действием усилия подачи G0 и силы резания FР и отделению элементов породы (стружки) передней гранью. При этом усилием подачи преодолевается сопротивление внедрению резца N1, а силой резания − сопротивление породы резаниюскалыванию N2 передней гранью резца (рис. 3.43).

После скалывания элемента породы по мере перемещения резца сопротивление породы N2 возрастает (рис. 3.44, I, II), и в момент превышения силой FР сопротивления породы происходит повторное отделение элементов − стружки (см. рис. 3.44, III). При дальнейшем перемещении резца процесс повторяется.

Как видим, процесс РГП характеризуется некоторой цикличностью и меняющимся уровнем затрачиваемой энергии в отдельные периоды работы породоразрушающего инструмента. При этом резцы производят периодически смятиескалывание элементов хрупкой породы передней гранью в нарастающем объеме до момента полного отрыва элементной стружки в пределах ширины забоя.

153

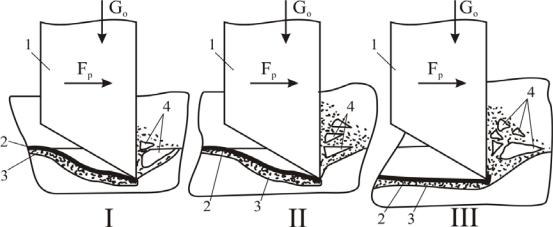
Рис. 3.44. Схема разрушения породы внедрившимся твёрдосплавным резцом при его перемещении в плоскости резания-скалывания под действием силы резания FР:

1 – резец; 2 – слой пластично деформируемой породы; 3 – слой раздавленной породы;

4 – элементы скалываемой породы; I, II, III – этапы работы резца

Таким образом, разрушение породы и отделение элементов стружки толщиной h будет иметь место при условии, что сила G0 превышает сопротивление породы N1, а сила резания FP превышает сопротивление породы разрушению-сдвигу (скалыванию) или отрыву, то есть силу N2, а также сопротивление сил трения лезвия резца о породу забоя ТЗ на передней грани ТПГ и его боковых гранях ТБГ (см. рис. 3.43). Силами трения ТБГ обычно пренебрегают в связи с очень малой их величиной.

Следовательно, разрушение породы при перемещении резца вдоль забоя, внедрившегося на глубину h, будет происходить при условии, что

Определим величину силы G0 , необходимую для внедрения резца. Сопротивление породы внедрению резца N1, как было показано ранее, определяется площадью контактной поверхности, в пределах которой происходит смятие-раздавливание породы SСМ, и твердостью породы PВ (3.75).

Но SСМ = аb. Тогда

где а − ширина площади притупления лезвия резца; b − длина лезвия; PВ − твердость породы.

Сила трения ТПГ определяется выражением (3.82):

TПГ = fN2 ,

154

где f − коэффициент трения отделяемых продуктов разрушения о переднюю грань резца; σСК − сопротивление породы скалыванию; b − ширина резца; hУП − глубина внедрения резца в установившемся периоде; γСК − угол скалывания породы.

Подставляя в выражение (3.96) найденные значения N1 (3.98) и TПГ (3.104), получим первое условие внедрения резца в породу:

Теперь определим второе условие резания-скалывания породы при перемещении резцов в плоскости забоя (3.97).

Величина силы N2 определена ранее найденным выражением (3.103). Сила трения резца о породу забоя ТЗ определяется выражением

Подставив в выражение (3.97) значения N2 (3.103) и TЗ (3.107), получим второе условие резания-скалывания породы резцом при его перемещении вдоль плоскости

Угол скалывания γСК по данным ряда исследователей составляет в среднем: для мягких пород – 30°; для пород средней твердости – 20° и для твердых – 15°.

Коэффициент трения резцов о породу зависит от целого ряда факторов: скорости вращения ПРИ, удельной нагрузки на резец и степени его износа, характера промывочной жидкости и т. д.

Профессор Б.И. Воздвиженский в своих работах приводит ориентировочные

155

Теоретическая оценка эффективности РГП при вращательном способе бурения скважин ПРИ кольцевой

формы с резцами из твердого сплава

Эффективность РГП при вращательном способе бурения скважин в конечном счете оценивается механической скоростью бурения, которая может быть определена теоретически для ПРИ с резцами из твердых сплавов в следующем упрощенном виде:

где hУП − толщина срезаемого (скалываемого) слоя породы; n − частота оборотов ПРИ; m − количество резцов в ПРИ.

Профессором В.С. Владиславлевым была предложена формула, полученная аналитическим путем, характеризующая глубину внедрения резца h:

где D − диаметр ПРИ; P − осевая нагрузка на резец; C − жесткость пары «резец– порода»; δ − ширина площадки притупления резца; σ − сопротивление породы разрушению; b − длина лезвия резца; μ − коэффициент трения резца о породу.

Но экспериментальные исследования не подтвердили адекватность получаемых данных по этой формуле практическим результатам.

Дело в том, что практически глубина внедрения резцов в установившемся режиме зависит от целого ряда факторов, неучтенных В.С. Владиславлевым. К их числу относятся: угол резания βP породы, скорость резания ω, степень износа резцов и др.

Исследованиями, проведенными на кафедре техники разведки ТПИ [24, 25, 26] установлено, что в зависимости от величины угла резания βP или переднего угла γП глубина внедрения резца существенно меняется.

Так, по данным В.И. Зварыгина [24, 25], при изменении γП от +60° до −60° при одном и том же уровне действующих сил (G0 = 20 даН; Fp = 40 даН) глубина внедрения уменьшается с 1,8 до 0,2 мм. Максимальная глубина внедрения в установившемся режиме резания в этом случае при значениях переднего угла γП = 0° −1,2

мм; +γП = 30° −1,5 мм и при + γП = 45…60° −1,7…1,8 мм (рис. 3.45).

Установленная зависимость может быть объяснена следующим образом. При изменении γП с положительного на отрицательный (рис. 3.46, а, б) площадь контакта резца с породой SК, по которой распределяется осевая нагрузка, увеличивается за счет площади контакта передней грани SКПГ. В результате этого при неизменной осевой нагрузке на резец величина удельного контактного давления уменьшается, а в разрушении породы будет превалировать процесс смятия-раздавливания над ска- лыванием-сдвигом, что, естественно, приводит к уменьшению масштабов разрушения породы и увеличению энергоемкости этого процесса.

Кроме того, с изменением угла резания меняется направление действия сил FН и F0 (см. рис. 3.46, а, б). Действительно, при + γП сила резания FР может быть разложена на две составляющих: нормальную к передней грани FН и касательную F0,

156

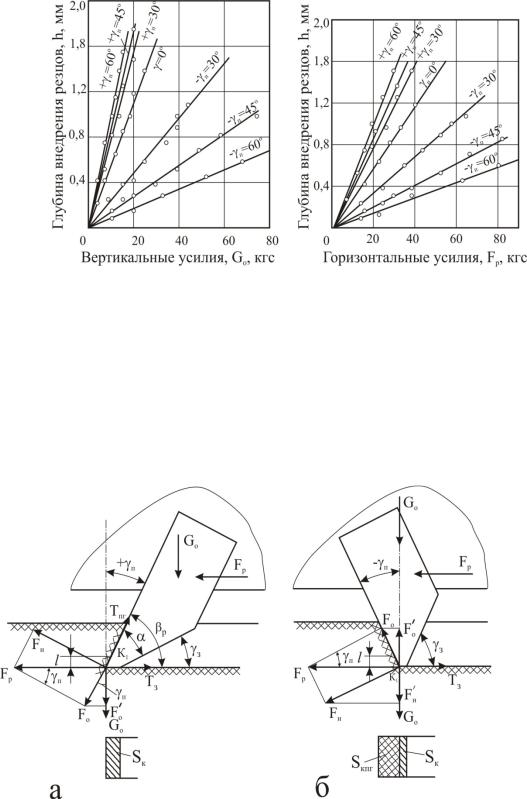
Рис. 3.45. Графики изменения глубины внедрения резцов с различными передними углами γП в зависимости от величины вертикальной Go и горизонтальной Fp сил резания-скалывания

Нормальная сила FН в этом случае работает на резание-скалывание, то есть на отрыв элемента породы в сторону свободной поверхности забоя, а сила F0 увеличивает действие осевой нагрузки, способствуя внедрению резца в породу. Проекция этой силы на вертикальную ось F0′ = F0cosγП. Подставив в это выражение значение

F0 (3.112), получим:

Рис. 3.46. Схема действия силы резания Fp при разных значениях переднего угла:

а – при положительном +γп; б – при отрицательном −γп

157

Как видим, эта сила не способствует разрушению породы, что снижает эффективность работы резцов с отрицательным углом резания.

Другая составляющая силы резания при –γ, нормальная FН, наоборот, способствует внедрению резца в породу. Ее проекция на вертикальную ось FН' направлена в сторону действия осевой нагрузки G0. Но работает она на сжатие породы с меньшей эффективностью, чем при положительном переднем угле.

Рис. 3.47. Графики изменения глубины h внедрения резцов различной ширины b в зависимости:

а – от осевой нагрузки Go; б – от величины силы резания Fp

Таким образом, чем больше величина отрицательного переднего угла, тем больше выталкивающая сила и тем больше должна быть осевая нагрузка для получения равной величины внедрения резца в породу, как это имеет место при положительном значении переднего угла. Однако в практической реализации твердосплавные коронки с положительным значением γП не нашли широкого применения из-за недостаточной механической прочности резцов и их износостойкости.

Исследованиями работы твердосплавных резцов установлено также влияние длины лезвия b (ширины резца) и геометрической формы его режущей части на усилие резания-скалывания породы (рис. 3.47 и 3.48).

158

Исследования, проведенные в ТПИ К.И. Борисовым [26], показали, что на величину hУП существенное влияние оказывают не только угол резания βР, но и скорость резания VP.

С учетом этого К.И. Борисовым была получена полуэмпирическая формула для определения величины hУП, имеющая вид

где G0 – удельная осевая нагрузка на резец; b − длина лезвия резца; σ − сопротивление породы внедрению резца; е − основание натурального логарифма; К − постоянный для данной породы показатель; VP − скорость резания; f − коэффициент трения; К1 − коэффициент, характеризующий положение точки приложения силы резания; ∆ − ширина площадки притупления резца.

Величина коэффициента К1 зависит от угла резания (переднего угла): чем больше расстояние l точки приложения силы FР от плоскости резания (см. рис. 3.46, б), тем менее эффективно работает резцовый инструмент. Величина коэффициента К1 определяется выражением

K1 = l12 .

Рис. 3.48. Графики изменения глубины h внедрения резцов в зависимости:

а– от геометрической формы режущей части;

б– от усилия осевой нагрузки Go; в – от силы резания Fp

159

Как видно из приведенных ранее рассуждений, при положительном значении переднего угла +γП эффективность процесса резания-скалывания больше, чем при отрицательном − γП или γП = 0.

Таким образом, эффективность работы твердосплавного резца можно характеризовать глубиной его внедрения h: при действии только осевой (статической) нагрузки G0 − hСТ ; при действии G0 и FР в неустановившемся (переходном) периоде − hНП (от 0 до max) и при установившемся периоде − hУП.

Используя формулу К.И. Борисова (3.116), можно прогнозировать механическую скорость углубки VМ при бурении твердосплавными многорезцовыми коронками, которая в общем случае определяется выражением (3.109). Подставив в это выражение значение hУП (3.116), получим более конкретную формулу прогнозирования механической скорости бурения:

Исследованиями, проведенными на кафедре техники разведки ТПИ, были установлены величины внедрения резца в породу, рассчитанные по формулам и полученные экспериментально К.И. Борисовым (табл. 3.4).

Как видно из приведенного материала, данные, полученные по формуле В.С. Владиславлева (3.110), многократно превышают величины hУП, полученные экспериментально и рассчитанные по формуле К.И. Борисова (3.116). Кроме того, из этих данных видно, что hСТ, полученная по формуле (3.95), существенно меньше полученных экспериментально.

Практически в процессе работы коронки за счет износа режущих элементов происходит изменение их геометрической формы с увеличением площадки притупления, что приводит к увеличению контактной поверхности SК, уменьшению контактного дав-

160