
БТЖ и ФРГП на весну 16 года / БТЖ - лекции_2015 / СулакшинЧубик
.pdf
К = 8,7266 107d4/(D2hl), |
(4.26) |
где D, h – соответcтвенно, диаметр и высота подвесного цилиндра, м; d, l – диаметр и длина рабочего участка упругой нити, м.
4.4.3. Реологические свойства
Реология является разделом физики, изучающим деформацию тел, в том числе их текучесть. Свое название она получила по предложению американского ученого Е. Бингама при основании им 29 апреля 1929 г. Реологического общества. Труды же по реологии появились на несколько лет раньше, а корень «rheo» (греч. «течение») нисходит еще к античности.
Толчком к развитию реологии как науки в 30-е годы нынешнего столетия послужила необходимость описания течения жидкостей, не обладающих постоянной вязкостью, т. е. тех, реологическое поведение которых не подчиняется закону Ньютона:
τ = μγ, |
(4.27) |
где τ – касательное напряжение сдвига, Па; |
μ – динамическая вязкость, Па с (при |
температуре 20,5 °С и давлении 0,1 МПа вязкость воды равна 1 мПа с); γ – скорость сдвига, с–1.
Реограмма, т. е. график зависимости τ = f(γ) ньютоновских (вязких) жидкостей (рис. 4.6), представляет собой прямую линию, проходящую через начало координат.
Из графика следует, что для ньютоновских жидкостей динамическая вязкость остается неизменной при любой скорости сдвига (в трубах, в затрубном пространстве, в насадках долота) и геометрически представляет собой тангенс угла наклона реологической кривой к
|
оси скорости сдвига. |
|
|
Жидкости, течение или реологиче- |
|
|
ское поведение которых не подчиняется |
|
Рис. 4.6. Реограмма |
закону внутреннего трения И. Ньютона, |
|
называются неньютоновскими. |
||
ньютоновской жидкости |
||
К таким жидкостям относятся мас- |
||
|
||
|
ляные краски, некоторые смазки, фарма- |
цевтические препараты, пищевые продукты, эмульсии, полимерные растворы, суспензии и др. К неньютоновским относится и большинство промывочных жидкостей.
Реологические свойства промывочных жидкостей ведущие отечественные и зарубежные специалисты относят к числу важнейших. Обусловлено это тем, что они оказывают существенное влияние практически на все показатели и процессы, связанные с бурением скважин. В частности, реологические свойства в значительной мере определяют степень очистки забоя скважины от шлама и охлаждения породоразрушающего инструмента, транспортирующую способность потока промывочной жидкости, величину гидравлических сопротивлений во всех звеньях циркуля-
231
ционной системы скважины и гидродинамического давления на ее стенки и забой в процессе бурения; амплитуду колебаний давления при пуске и остановке насосов, выполнении СПО и проработке скважины с расхаживанием бурильной колонны; интенсивность обогащения промывочной жидкости шламом, полноту ее замещения тампонажным раствором в кольцевом пространстве между обсадной колонной и стенками скважины и др.
Перечень показателей, которыми характеризуют реологические свойства промывочных жидкостей, определяется выбором реологической модели, т. е. уравнения, описывающего связь между возникающими в жидкости напряжениями τ и скоростью ее деформации или сдвига γ.
Первой реологической моделью, использованной для описания реологического поведения глинистых суспензий (В. Грегори, 1927 г.), была модель, которая в нашей стране известна как модель Бингама–Шведова:
τ = τ0 + γη, |
(4.28) |
где τ0 – динамическое напряжение сдвига, Па; η – пластическая вязкость, Па с. Динамическое напряжение сдвига косвенно характеризует сопротивление
промывочной жидкости, возникающее при инициировании ее течения. С увеличением динамического напряжения сдвига увеличивается удерживающая способность промывочной жидкости, но вместе с тем возрастают гидравлические сопротивления в циркуляционной системе скважины, амплитуда колебаний давления при пуске и остановке насосов и выполнении СПО, а также вероятность образования застойных зон с аккумуляцией в них выбуренной породы.
Пластическая вязкость промывочной жидкости характеризует темп роста касательных напряжений сдвига при увеличении скорости сдвига.
С увеличением пластической вязкости возрастают гидравлические сопротивления в циркуляционной системе скважины и снижается ресурс работы буровых насосов, а также доля гидравлической мощности, подводимой к забойному двигателю и долоту.
Двухпараметрическая линейная модель (4.28) была предложена Е. Бингамом в 1921 г. (по другим источникам в 1916 г.) для описания реологического поведения красок, аномально отличающегося от поведения ньютоновских жидкостей зависимостью вязкости от скорости сдвига. Такого же рода аномалия у растворов желатина была обнаружена русским ученым Шведовым Ф.Н. еще в 1898 г. (по другим источникам в 1885 г.).
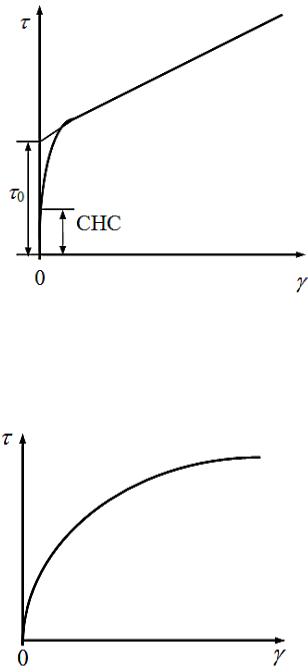
Промывочные жидкости, реологическое поведение которых описывается уравнением (4.28), называются вязкопластичными. Для реальных промывочных жидкостей при малых скоростях сдвига зависимость τ = τ(γ) нелинейна, что не соответствует модели Бингама–Шведова. Однако этот интервал скоростей сдвига во внимание не принимается и динамическим напряжением сдвига τ0 считается значение напряжения в точке пересечения продолжения прямой τ = τ(γ) с осью касательных напряжений (рис. 4.7). Отсюда следует, что динамическое напряжение сдвига имеет скорее математическую, чем физическую интерпретацию. Действительное же напряжение, при котором начинается течение жидкости, меньше, чем τ0, и называется статическим напряжением сдвига (СНС).
232
|
Таким образом, вязкопластичная |
||||
|
промывочная |
жидкость |
характеризу- |
||
|
ется тем, что в состоянии покоя обла- |
||||
|
дает пространственной |
структурой, |
|||
|
достаточно жесткой, чтобы сопротив- |
||||
|
ляться любому напряжению, меньше- |
||||
|
му СНС. Когда напряжение сдвига τ, |
||||
|
вызванное внешним |
воздействием, |
|||
|
превышает значение СНС, структура |
||||
|
разрушается |
и жидкость |
начинает |
||
|
течь. При τ > τ0 жидкость течет уже |
||||
|
как обычная ньютоновская жидкость с |
||||
|
вязкостью η. Когда действующие в |
||||
|
промывочной |
жидкости касательные |
|||
|
напряжения сдвига становятся меньше |
||||
|
СНС (τ < СНС), то пространственная |
||||
Рис. 4.7. Реограмма |
структура вновь восстанавливается. |
||||
В начале 50-х годов для описа- |
|||||
вязкопластичной жидкости |
|||||
ния реологического поведения про- |
|||||
|
|||||
|
мывочных жидкостей наряду с моде- |
||||
лью Бингама–Шведова стала использоваться приведенная ниже степенная |
двухпа- |
||||
раметрическая модель, которая впервые была получена В. Оствальдом и де Ваале в 1925 г. и соответственно носит название модели Оствальда–де Ваале (рис. 4.8):
τ = k(γ)n, |
(4.29) |
где k – показатель консистенции при γ = 1 с–1, Па с; n – показатель неньютоновского поведения.
Показатель консистенции характеризует густоту или вязкость промывочной жидкости. С увеличением показателя консистенции увеличивается ее транспортирующая и удерживающая способность, но вместе с тем увеличиваются и гидравлические сопротивления в циркуляционной системе скважины, а также амплитуда колебаний давления при инициировании те-
чения промывочной жидкости и выполнении СПО, что повышает вероятность возникновения гидроразрывов пластов и газонефтеводопроявлений.
Показатель неньютоновского поведения промывочной жидкости характеризует степень отклонения ее реологического поведения от поведения ньютоновских жидкостей. Снижение значений показателя неньютоновского поведения вызывает выполаживание эпюры скоростей потока промывочной жидкости в кольцевом пространстве скважины, в результате чего повышается ее транспортирующая способность, так как основная масса шлама оказывается в зоне максимальных скоростей.
233
Появление степенной модели (4.29) в буровой реологии было обусловлено ее способностью учитывать нелинейность кривых течения промывочных жидкостей, обработанных химическими реагентами, в частности полимерами, а также возросшим ассортиментом последних.
Промывочные жидкости, реологическое поведение которых описывается моделью Оствальда–де Ваале, называются псевдопластичными. Для них характерно снижение вязкости с увеличением скорости сдвига, что объясняется выравниванием, ориентированием взвешенных несимметричных твердых частиц суспензий и развертыванием цепей полимеров таким образом, что течению оказывается минимальное сопротивление.
В нашей стране модель Оствальда–де Ваале впервые была использована для описания реологического поведения промывочных жидкостей Б. Филатовым и Чжу Мэ в 1960 г.
Итак, в отечественной и зарубежной практике наиболее широко используемыми являются двухпараметрические модели Бингама–Шведова и Оствальда–де Ваале. Однозначное мнение о том, какая из моделей, Оствальда–де Ваале или Бингама–Шведова, является наиболее предпочтительной для описания реологического поведения неньютоновских промывочных жидкостей, до сих пор отсутствует. Поэтому к выбору этих моделей и, следовательно, к выбору перечня показателей, характеризующих реологические свойства промывочных жидкостей, существует три различныхподхода.
1.Априорный, или эвристический подход, когда реологические свойства промывочной жидкости характеризуют либо пластической вязкостью и динамическим напряжением сдвига, либо показателями консистенции и неньютоновского поведения, т. е. когда без каких-либо обоснований в качестве базовой принимают или модель Бингама–Шведова, или модель Оствальда–де Ваале. Очевидно, что при таком подходе реологические свойства промывочных жидкостей даже одного и того же типа и состава могут характеризоваться совершенно разными показателями, что исключает возможность сопоставления, сравнительной количественной оценки и выбора наиболее предпочтительных из них с позиций реологии.
2.Статистический подход, когда реологические свойства промывочной жидкости характеризуют показателями той из двух рассматриваемых моделей, которая наиболее адекватно, т. е. с меньшей погрешностью, описывает ее реологическое поведение. Однако реологическое поведение промывочной жидкости одного и того же компонентного состава в зависимости от ее долевого состава, температуры и диапазона скоростей сдвига может адекватно описываться то моделью Бингама–Шведова, то моделью Оствальда–де Ваале, в связи с чем при бурении разных по глубине интервалов одной и той же скважины реологические свойства промывочной жидкости необходимо характеризовать то одним, то другим комплексом несопоставимых друг
сдругом показателей.
3.Компромиссный подход, когда реологические свойства промывочной жидкости одновременно оценивают показателями, входящими в модель Бингама– Шведова и Оствальда–де Ваале.
Кроме основных параметров этих моделей (τ0, η, k, n), для характеристики реологических свойств промывочных жидкостей широко используют ещё и целый ряд дополнительных: коэффициент пластичности, эффективную вязкость при скорости сдвига равной 100 с–1, асимптотическую вязкость, или эффективную вязкость, при полностью разрушенной структуре (при скорости сдвига равной 10 000 с–1).
234
Коэффициент пластичности промывочной жидкости (КП, с–1) определяется величиной отношения динамического напряжения сдвига к пластической вязкости:
КП = τ0 /η. |
(4.30) |
С ростом коэффициента пластичности увеличивается транспортирующая способность потока, а также гидродинамическое давление струй промывочной жидкости, выходящих из насадок долота, что обеспечивает более эффективное разрушение горных пород на забое и рост механической скорости бурения. При этом высокие значения коэффициента пластичности желательно поддерживать за счет снижения пластической вязкости промывочной жидкости, а не увеличения ее динамического напряжения сдвига.
Эффективная вязкость (ЭВ) характеризует ту действительную вязкость, котopoй обладает промывочная жидкость при скорости сдвига, имеющей место в кольцевом пространстве скважины, в бурильных трубах или в промывочных каналах породоразрушающего инструмента. Она является общим показателем реологических свойств промывочных жидкостей, независимо от того, какой моделью описывается их реологическое поведение.
Величина эффективной вязкости определяется по следующим формулам:
•для вязкопластичных промывочных жидкостей
ЭВ = η + (τ0Dэ/6υ); |
(4.31) |
•для псевдопластичных промывочных жидкостей
ЭВ = k(γw)n–1, |
(4.32) |
где Dэ – эквивалентный диаметр канала потока промывочной жидкости, м (в бурильных трубах Dэ = d1, где d1 – внутренний диаметр бурильных труб; в кольцевом пространстве скважины Dэ = D – d2, где D – диаметр скважины, d2 – наружный диаметр бурильных труб; в промывочных каналах породоразрушающего инструмента Dэ = 4F/П, где F – суммарная площадь сечения промывочных каналов, П – полный смоченный периметр промывочных каналов); υ – средняя по сечению канала потока объемная скорость движения промывочной жидкости, м/с (в бурильных трубах υ = 4 10–3Q/60πd12, где Q – расход промывочной жидкости, дм3/мин; в кольцевом пространстве скважины υ = 4 10–3Q/60π(D2 – d22); в промывочных каналах коронок υ = Q 10–3/60kbh, где k – число промывочных каналов, b – ширина промывочного канала, h – начальная глубина промывочного канала); γw – скорость сдвига в интересующем исследователя канале скважины, с–1.
В циркуляционной системе скважины скорость сдвига меняется в очень широких пределах: в бурильной колонне от 100 до 500 с–1, в УБТ от 700 до 3000 с–1; в
затрубном кольцевом пространстве от 10 до 500 с–1, чаще всего 100 с–1; в насадках долот от 10 000 до 100 000 с–1.
Значение скорости сдвига в бурильных трубах и промывочных каналах породоразрушающего инструмента может быть рассчитано по следующей формуле:
235
γw = [(3n + 1)/4n](8υ/D). |
(4.33) |
В кольцевом пространстве скважины скорость сдвига
γw = [(2n + 1)/3n] [12υ/(Dс – d2)]. |
(4.34) |
Таким образом, по приведенным выше формулам эффективная вязкость (ЭВ) может быть рассчитана не только для принятых в качестве стандартных скоростей сдвига (100 и 10 000 с–1), но и для тех скоростей сдвига γw, которые действительно имеют место в том или ином канале циркуляционной системы скважины.
Эффективная вязкость при скорости сдвига равной 100 с–1 (ЭВ100, Па с) характеризует вязкость промывочной жидкости в кольцевом пространстве скважины и является основным показателем, определяющим транспортирующую способность её потока, которая тем выше, чем выше значения ЭВ100. Вместе с тем с ростом ЭВ100 увеличиваются гидравлические сопротивления при течении промывочной жидкости в кольцевом пространстве и, соответственно, дифференциальное давление, что ведет к снижению механической скорости бурения и проходки на долото (коронку) в результате не только удержания частиц разрушенной породы на забое, но и ухудшения условий формирования зоны предразрушения (условий зарождения и развития макро- и микротрещин):
ЭВ100 = k(100)n–1. |
(4.35) |
Эффективная вязкость при полностью разрушенной структуре (ЭВ∞) характеризует вязкость промывочной жидкости в промывочных каналах породоразрушающего инструмента и в пескоилоотделителях (гидроциклонах). С уменьшением ЭВ∞ повышается степень очистки забоя скважины от шлама и охлаждения вооружения породоразрущающего инстумента, вследствие чего возрастает ресурс его работы и механическая скорость бурения. Кроме того, с уменьшением ЭВ∞ снижается интенсивность обогащения промывочной жидкости шламом, так как при меньшей вязкости последний легче отделяется в очистных устройствах:
ЭВ∞ = k (10 000)n–1. |
(4.36) |
Очевидно, что компромиссный подход к выбору реологической модели, т. е. использование семи показателей (τ0, η, k, n, КП, ЭВ100, ЭВ∞) позволяет достаточно всесторонне охарактеризовать реологические свойства и связанные с ними функциональные возможности промывочной жидкости. Однако, если на этапе её проектирования это является достоинством, то в процессе эксплуатации промывочной жидкости, напротив, становится недостатком, так как одновременно контролировать большое число показателей, а главное управлять ими чрезвычайно сложно.
Экспериментально доказано, что для оценки реологических свойств буровых растворов вполне достаточно использовать комплекс из трех показателей: пластическая вязкость (η, мПа с), динамическое напряжение сдвига (τ0, дПа) и коэффициент пластичности (КП, с–1), которые и предлагается повсеместно использовать для характеристики реологических свойств промывочных жидкостей на водной основе.
236
Чтобы установить характер зависимости между касательными напряжениями и скоростями сдвига и определить значения показателей реологических свойств промывочных жидкостей используют капиллярные и ротационные вискозиметры, последние из которых используются гораздо чаще.
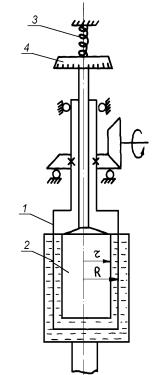
Основу ротационного вискозиметра (pиc. 4.9) составляют два вертикально расположенных соосных цилиндра, в зазор между которыми заливается исследуемая промывочная жидкость.
|
Внешний цилиндр (гильза) 1 может вращаться с раз- |
|
личными частотами. При вращении гильзы между концен- |
|
трическими слоями промывочной жидкости, находящейся в |
|
кольцевом зазоре вискозиметра, возникают касательные |
|
напряжения сдвига и обусловленный ими крутящий мо- |
|
мент, который передается внутреннему цилиндру (измери- |
|
тельному элементу) 2. В результате последний поворачива- |
|
ется вокруг своей оси до тех пор, пока момент, развивае- |
|
мый касательными напряжениями сдвига, не станет равным |
|
моменту закручивания пружины 3. Угол поворота измери- |
|
тельного элемента, пропорциональный величине касатель- |
|
ных напряжений сдвига, фиксируется по шкале прибора 4. |
|
Устройство ротационного вискозиметра и порядок |
|
работы с ним рассмотрим на примере отечественного при- |
|
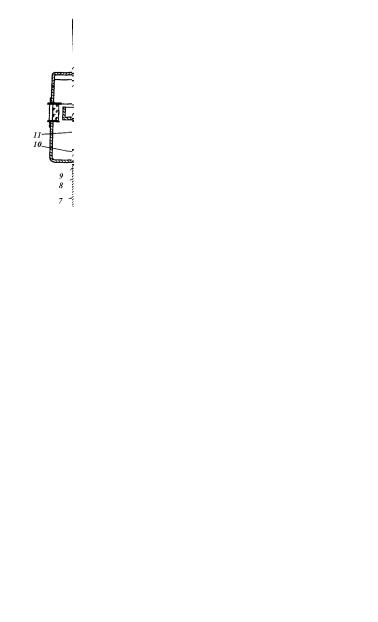
бора ВСН-3 (рис. 4.10), состоящего из сборного корпуса, |
|
измерительной системы, привода и пробоотборника для |
|
измеряемой жидкости. |
|
Корпус состоит из кожуха 2, оснований 17, 19, верх- |
|
ней платы 9, нижней платы 1 и крышек 12 и 27. На платах |
|
смонтированы все механизмы вискозиметра. |
|
Измерительная система крепится к верхней плате 9 и |
Рис. 4.9. Общая |
состоит из измерительного элемента 3, закрепленного на |
схема ротационного |
оси 7, которая установлена на двух керновых опорах 4 и 11. |
вискозиметра |
Для регулирования осевого зазора подпятник опоры 11 за- |
|
креплен в винте, перемещающемся во втулке 10. На втулке |
10 смонтированы подшипники 22.
На наружных обоймах этих подшипников посажена шпиндель-шестерня 8, передающая вращение гильзе 5. На верхней части оси 7 установлена втулка 23, на которой закреплены шкала и один конец измерительной пружины 21. Другой конец пружины закреплен в винте 20, который перемещается в кронштейне 18.
Привод вискозиметра имеет пять частот вращения: 0,2; 200; 300; 400 и 600 мин–1 и состоит из электродвигателя 28, двухскоростного двигателя 13, муфт обгона 16, 24, блока шестерни 15, шестерен 6, 8, 14, 25, 26, 29, 30, 32 и вала 31.
Техническая характеристика ВСН-3 |
|
Пределы измерения касательных напряжений сдвига, Па: |
|
для пружины № 1 ................................................................................................ |
0…45 |
для пружины № 2 ................................................................................................ |
0…90 |
Диапазон измерений динамической вязкости ньютоновских |
|
жидкостей (при 200 мин–1), Па с: |
|
для пружины № 1 ........................................................................................ |
0,001…0,2 |
237
для пружины № 2 .............................................. ................. |
.................. |
....... 0,001… 0,4 |
Частота вращения гильзы, мин–1.......................... ...................... |
0,2; 200 ; 300; 400; 600 |
|
Максимальный угол поворота измерительного элемента .........., град |
.................. .270 |
|
Наружный диаметр измерительного элемента, мм............................... |
................ |
39,62 |
Высота измерительного элемента, м м................. ................................... |
..................... |
60 |
Внутренний диаметр гильзы, мм......................... ................................... |
..................... |
44 |
Потребляемая мощность, В А.............................. ................................... |
..................... |
65 |
Пределы термостатирования исследуемой жидк ости, °С.................... |
............. |
20 …60 |
Габаритные размеры, мм...................................... ................................... |
.. |
278×192× 525 |
Масса, кг................................................................. ................................... |
..................... |
19 |
Питание от сети переменного тока напряжением 220 В при частоте 50 Гц. |
||
Рис. 4.10. Ротационный вискозиметр ВСН-3
238
Реометрические измерения на ротационном вискозиметре BCH-3 сводятся к последовательной установке фиксированных частот вращения гильзы ni (600, 400, 300 и 200 мин–1) и определению при этом устойчивых показаний углов поворота
шкалы ϕi.
Реометрию промывочных жидкостей с помощью ВСН-3 необходимо проводить в следующем порядке:
1.Установить ВСН-3 на столе, не подвергающемся вибрациям и тряске.
2.Проверить «нуль» шкалы прибора. При несовпадении «нуля» шкалы с визирной линией на смотровом стекле установить «нуль» шкалы, руководствуясь при этом инструкцией по эксплуатации ВСН-3.
3.Поставить тумблер в положение «откл» и включить вилку прибора в сеть переменного тока напряжением 220 В и частотой 50 Гц.
4.Надеть гильзу на шпиндель-шестерню, налить в стакан до риски испытуемую промывочную жидкость и установить стакан на телескопический столик.
5.Измерить температуру испытуемой промывочной жидкости с точностью до ближайшего деления термометра.
При проведении реометрии без предварительного термостатирования промы-
вочной жидкости ее температура должна составлять 21 ± 3 °С.
6. В тех случаях, когда температура промывочной жидкости не соответствует указанной в п. 5 или требуется оценить ее реологические свойства при повышенной температуре (максимум до 60 °С), необходимо подсоединить стакан к термостату резиновыми шлангами и выдержать испытуемую промывочную жидкость до достижения заданной температуры.
7.Поднять телескопический столик и зафиксировать его в верхнем положении поворотом по часовой стрелке.
8.Установить переключатель частот вращения гильзы в положение 600 мин–1, тумблер в положение «вкл» и перемешать испытуемую промывочную жидкость в течение 5 мин с целью разрушения в ней тиксотропной структуры.
9.Дождаться устойчивого, не изменяющегося при вращающейся гильзе в течение 1 мин положения шкалы прибора и взять отсчет с точностью до 1/2 деления шкалы. Повторить измерения 1–2 раза при той же частоте вращения гильзы.
10.Провести измерения согласно п. 9 при частотах вращения гильзы, равных
400, 300, 200 мин–1.
П р и м е ч а н и я
1.Измерения от момента окончания перемешивания промывочной жидкости
по п. 8 и до момента снятия последнего повторного отсчета при частоте вращения гильзы, равной 200 мин–1, должны проводиться непрерывно с минимально возможной продолжительностью для того, чтобы исключить тиксотропное схватывание и потерю устойчивости промывочной жидкости под действием центробежных и гравитационных сил.
2.При зашкаливании прибора, оснащенного пружиной № 1, на частоте вращения гильзы, равной 600 мин–1, необходимо продолжить измерения, перейдя на частоту 400 мин–1, а при зашкаливании прибора и на этой частоте проводить измерения на всех частотах, используя пружину № 2.
3.При значениях угла поворота шкалы прибора, оснащенного пружиной № 1, составляющих менее 10° на частоте вращения гильзы, равной 200 мин–1, результаты
239
измерений на этой частоте в последующие расчеты не включать, а в той же ситуации на частоте 300 мин–1 использовать для измерений на всех частотах нестандартную пружину меньшей жесткости.
Это требование обусловлено тем, что работа в диапазоне углов поворота шкалы ВСН-3 от 0 до 10° приводит к большим погрешностям оценки показателей реологических свойств.
4. Во всех случаях реометрию на ВСН-3 необходимо проводить не менее чем при трех различных частотах вращения гильзы.
По окончании реометрии производится расчет касательных напряжений и скоростей сдвига при всех использованных в процессе измерений частотах вращения гильзы.
Для перевода показаний, снимаемых по шкале BCH-3, в термины касательных напряжений сдвига зафиксированные значения углов поворота шкалы умножаются на паспортную константу К прибора:
τi = Kϕi, |
(4.37) |
где τi – касательное напряжение сдвига при i-й частоте вращения гильзы, Па; ϕi – средний (по 2–3 параллельным измерениям) угол поворота шкалы прибора при той же частоте вращения гильзы, град; К – константа прибора, Па/град.
Скорость сдвига в кольцевом зазоре вискозиметра при i-й частоте вращения гильзы приближенно может быть найдена по формуле
γi = πn/1[1 – (r/R)2], |
(4.38) |
где γi – скорость сдвига, с–1, при частоте вращения гильзы ni, мин–1; r – радиус измерительного элемента, мм; R – внутренний радиус гильзы, мм.
Величины r и R определяются по данным технической характеристики прибора или более точно путем непосредственного измерения штангенциркулем с ценой деления 0,02 мм.
Значения констант К для пружин № 1 и 2, входящих в комплект прибора ВСН-3, приводятся в руководстве по его эксплуатации.
Константа К с достаточно высокой точностью может быть определена расчетным путем по формуле
К = (d4Е)/[23040r2h(Dн – d)i], |
(4.39) |
где Dн – наружный диаметр пружины, м; i – число рабочих витков пружины; Е – модуль упругости (для пружинных сталей Е = 2,1 1011 Па); d – диаметр проволоки, м; r – радиус измерительного элемента, м; h – высота измерительного элемента, м. (расставить).
Многочисленные экспериментальные исследования свидетельствуют о том, что реологическое поведение промывочных жидкостей существенно зависит от температуры и давления.
Так, по мере увеличения температуры в глинистых суспензиях происходит следующее:
240
