БТЖ и ФРГП на весну 16 года / БТЖ - лекции_2015 / СулакшинЧубик

деформацию упругопластично-хрупкой породы AУП, также определяется по диаграмме деформации (рис. 3.26, б). Величина работы, затрачиваемой на деформацию породы, в этом случае определяется площадью фигуры ОВДЕ.

Рис. 3.26. Графики деформации горных пород δ при внедрении индентора под действием нагрузки Р:

а − упругохрупкой; б − упругопластично-хрупкой; в − пластичной

Кроме того, эта работа может быть вычислена аналитически с использованием коэффициента пластичности KПЛ и работы, затрачиваемой на упругую деформацию AУП этой породы:

где KПЛ – коэффициент пластичности породы.

Наконец, работа, затрачиваемая на деформацию чисто пластической породы AПЛ, может быть определена по графику деформации такой породы (рис. 3.26, в) путем вычисления площади ОА'С, получаемой при внедрении индентора на условную глубину 5 мм.

Удельная работа, затрачиваемая при РГП

При исследованиях процесса РГП обычно определяют «удельную объемную» или «контактную» величину работы разрушения при одинаковых условиях, что позволяет делать сравнительную оценку эффективности того или иного способа РГП.

Удельная объемная работа разрушения определяется отношением общей работы, затраченной при разрушении АОБЩ, кГс·м/см3, к объему разрушенной породы (лунки) VP, см3:

УдельнаяконтактнаяработаразрушенияАУК, кГс·м/см2, определяетсявыражением

где SК − площадь контактной поверхности.

При определении показателя эффективности РГП прибегают к помощи коэффициента полезного действия η, который определяется отношением полезной работы процесса РГП AПРП к работе, затрачиваемой до разрушения породы:

131

Величина этого коэффициента, по данным профессора Л.А. Шрейнера, при механических способах разрушения горных пород не превышает 0,01 %. Такая низкая величина КПД объясняется большим расходом энергии на повышение температуры породы, породоразрушающего инструмента и окружающей среды.

Работа, расходуемая на разрушение (диспергирование) горной породы, может быть оценена при помощи известного закона Риттингера: «Работа, затраченная на дробление (разрушение) породы, пропорциональна вновь полученной поверхности измельченного материала или степени его измельчения».

3.2.Разрушение горных пород

при механических способах бурения скважин

3.2.1. Разрушение горных пород инструментом дробяще-скалывающего действия

при ударном способе бурении скважин

Ударное бурение скважин является древнейшим способом. Первые упоминания о бурении скважины ударным способом датируются 3 тыс. до н. э. В Китае, Египте и в Древней Руси скважины использовались с целью водоснабжения и добычи соляных растворов. Это были несложные деревянные или бамбуковые буровые штанги для спуска в скважину породоразрушающего инструмента в виде зубила. При этом использовались грузоподъемные приспособления в виде балансиров или лебедок-воротов (рис. 3.27).

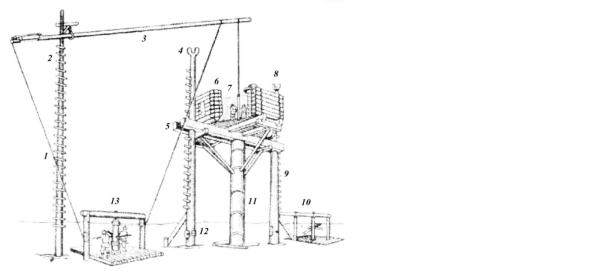
Рис. 3.27. Установка для бурения под рассолоподъемную трубу на Балахновском Усолье:

1 – канат; 2 – очап; 3 – коромысло; 4 – соха; 5 – переклад; 6 – изба (укрытие); 7 – штанга;

8 – развилка для привязанных блоков; 9 – лестница; 10, 13 – вороты с блоками для

спуска труб и буровых операций; 11 – обсадная труба; 12 – матица

В практике этот способ бурения применялся в разных вариантах: с использованием бурильных труб или каната (троса) при спуске и подъеме ПРИ.

132

Применение бурильных труб позволяло осуществить принудительное сбрасывание бурового снаряда с увеличением частоты ударов, наносимых буровым снарядом. При использовании каната частота ударов ограничивалась скоростью падения бурового снаряда.

Продукты разрушения заливались водой и вычерпывались ведром (желонкой).

3.2.2. Конструктивные элементы и условия применения породоразрушающего инструмента дробяще-скалывающего действия

Породоразрушающие инструменты (ПРИ) или долота дробяще-скалывающего действия (ДрСкД), применяемые при ударном бурении, имеют вид лопасти с клиновой формой породоразрушающего элемента (рис. 3.28, а). Основными конструктивными элементами таких долот являются: лезвие, щёки, лопасть или корпус долота, резьбовая головка для присоединения к буровому снаряду.

Лезвие долота образуют две грани − щеки, угол между которыми α называется углом приострения. Длина лезвия D характеризует диаметр формирующейся скважины. Этот параметр условно принято считать диаметром долота.

Лезвия могут иметь форму прямой или изогнутой линии, угол наклона которой γ может быть, соответственно, равным нулю (при прямой форме лезвия), отрицательным (при вогнутой форме) и положительным (при выпуклой). Различным может быть и количество лезвий: одно, два, три и более. Обычно одно является основным, а остальные − дополнительными или боковыми (рис. 3.28, б–д).

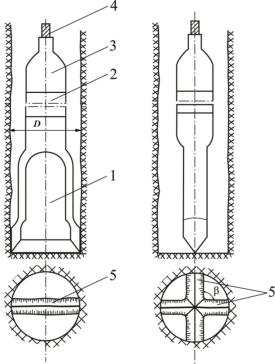
Рис. 3.28. Общий вид и конструктивные элементы долота для ударного способа разрушения пород:

1 – долото;

2 – буровая штанга;

3 – канатный замок;

4 – канат;

5 – забой

Долота с одним лезвием называют плоскими (оставляют при ударе след прямой линии); с двумя − крестовыми (след в виде двух прямых линий, пересекающих-

133

ся под прямым углом); с одним основным и двумя дополнительными − двутавровыми или зетобразными (след имеет вид двутавра или буквы зет).

При ударном способе бурения разрушение породы обычно происходит вследствие нанесения ударов по забою специальным буровым снарядом с долотом той или иной конструкции (рис. 3.29).

Рис. 3.29. Схема конструктивных элементов породоразрушающих инструментов для ударного способа РГП при канатном бурении скважин:

1 – лезвие долота; 2 – щеки долота; 3 – корпус долота; 4 – резьбовое соединение; а, б – тело и след от удара плоским долотом; в – след от удара крестового долота; г – след от удара двутаврового долота; д – след от удара z-образного долота

Породоразрушающий инструмент в этом случае, утяжелённый ударной штангой, сбрасывается с некоторой высоты после подъёма с помощью специального механизма и, нанося удар по забою, разрушает породу. После каждого удара снаряд поднимается на небольшую высоту и поворачивается на некоторый угол β (рис. 3.29) без разрушения породы. Поэтому такой способ бурения называют удар- но-поворотным (в отличие от ударно-вращательного).

Удары могут наноситься по ПРИ и без его подъёма – с помощью специального ударного устройства. Такой способ называется ударно-забивным. Он реализуется обычно при бурении скважин в достаточно мягких породах.

Ударный снаряд может быть подвешен на канате или на колонне бурильных труб. В первом случае бурение называется ещё и ударно-канатным, а во втором − ударно-штанговым.

3.2.3. Теоретические основы разрушения горных пород инструментом дробяще-скалывающего действия клиновой формы

Усилия, разрушающие породу при ударном бурении, как было сказано, носят динамический характер, а разрушение происходит за счёт дробления, смятия и скалывания некоторых элементов породы.

134

При внедрении лезвия долота в твёрдую хрупкую породу под его торцом порода дробится, а частицы разрушенной породы вытесняются из-под торца ПРИ или спрессовываются.

По обе стороны лезвия происходит скалывание некоторых элементов хрупкой породы за пределами контактной поверхности (рис. 3.30).

Рис. 3.30. Схема разрушения хрупкой (а) и пластичной (б) породы при ударном бурении скважин:

1 − уплотненная раздробленная или пластически деформируемая порода; 2 − частицы скалываемой породы; 3 − пластически деформируемая и вытесняемая из лунки порода; в – план забоя: 1 – разрушение породы в контакте щек лезвия долота; 2 – площадки скалывания породы за пределами контактной площади; 3 – площади возможного

дополнительного скалывания породы при повторных ударах

В этом случае объём разрушенной породы будет больше объёма внедрившейся части долота, а глубина лунки h1, с учётом разрушенной уплотнённой породы, больше глубины внедрения лезвия долота h.

При внедрении в более мягкую вязкопластичную породу происходит смятие, уплотнение и вытеснение породы внедрившейся частью долота (рис. 3.30, б). При этом возникают пластические деформации, а скалывание происходит в значительно меньшем объёме или совсем не происходит. Часть породы вытесняется долотом из лунки без разрыва связей. Объём образующегося углубления соответствует при этом объёму внедрившейся части долота.

Время нагружения tн инструмента при таком способе разрушения весьма незначительно. Практически оно составляет всего лишь 0,003…0,005 с. Следовательно, при частоте ударов порядка 50 в минуту долото воздействует на забой в момент удара всего только в течение 0,15…0,25 с.

Сила удара может достигать значительных величин за счёт массы снаряда и скорости его соударения. Поэтому при ударном способе бурения с помощью долот из прочной стали можно разрушать достаточно твёрдые породы. Но механическая скорость бурения при этом невелика в связи с малым числом ударов в единицу времени (обычно частота ударов 50…60 мин–1) по технологическим причинам.

Для разрушения породы по всей площади дна скважины (площадь круга) долотом следует нанести серию ударов (см. рис. 3.29, а). При этом в определённых условиях порода в промежутках между углублениями, полученными при нанесении ударов, скалывается.

135

Разрушение горных пород при ударном бурении определяется, таким образом, целым рядом факторов: силой удара Р, количеством ударов m, наносимых по забою для его углубки на некоторую величину h, и величиной угла поворота долота β после каждого удара.

От силы удара зависит глубина внедрения долота h, а от количества ударов m и угла поворота β − скорость углубки скважины или продвижения забоя VМ.

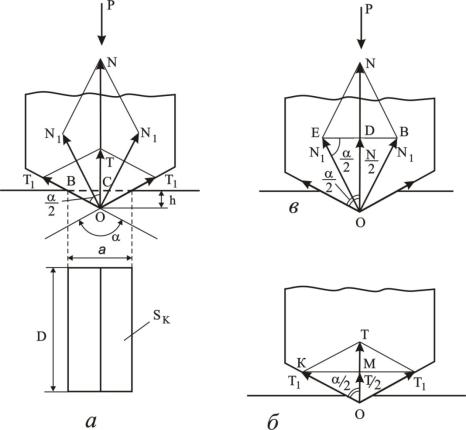
Рис. 3.31. Схема действия сил при внедрении долота в породу

Теория РГП при ударном способе бурения, предложенная в своё время профессором Н.С. Успенским и использованная в работах проф. Б.И. Воздвиженского и других учёных, сводится к следующему (рис. 3.31, а).

При ударе с силой Р лезвие долота внедряется на глубину h. В этом случае происходит дробление и смятие породы на площади контакта щек долота с забоем SК, величина которой в проекции на плоскость забоя определяется выражением

где D − длина лезвия долота (диаметр скважины); а − ширина площадки разрушаемой породы долотом; SК − площадь дробления-смятия породы.

В этом случае долото преодолевает в конечном итоге сопротивление породы разрушению − силу N и сопротивление силы трения Т, которые являются равнодействующими соответственно сил N1 и Т1, направленных против действия силы Р на каждой из щёк долота.

136

Из чертежа на рис. 3.31, а видно, что сторона ВС треугольника ОСВ имеет величину а/2, а сторона ОС = h − глубине внедрения долота. Следовательно, можно записать:

где α − угол приострения лезвия долота.

Подставив значение а в формулу (3.46), получим величину силы N:

Теперь определим величину силы трения Т из прямоугольного треугольника ОМК (см. рис. 3.31, б), у которого стороны ОМ = Т/2, а ОК = Т1. Следовательно, можно записать:

Но сила трения Т1, действующая на одной щеке лезвия долота, определяется силой её прижатия N1 к породе при ударе и величиной коэффициента трения f щёк долота о породу забоя:

где N1 − сила реакции породы при внедрении лезвия долота. Силу N1 находим из треугольника ОDЕ (см. рис. 3.31, в):

откуда

N1 = 2sinN α .

2

Подставив сюда значение силы N, найденное ранее (3.49), и сделав преобразования, будем иметь:

137

Подставив найденное значение силы N1 (3.54) в выражение (3.52), определяем величину Т1:

= fhDσ

T1 cos αСЖ . (3.55) 2

Подставив это выражение в уравнение (3.51), находим общую величину силы трения Т:

Найденные значения сил N (3.49) и T (3.56) подставляем в исходное выражение (3.44), определяющее главное условие разрушения породы

PД = N +T = 2hDσСЖtg α2 = 2 fhDσСЖ

или

Из этого выражения находим величину внедрения долота в породу h:

Отсюда видно, что глубина внедрения долота в породу тем больше, чем больше сила удара и чем меньше диаметр долота D и сопротивление породы разрушению σСЖ, а также зависит от угла приострения долота α и коэффициента трения f.

Но полученное выражение (3.58) справедливо только для плоских долот простейшей конструкции. При ударно-канатном бурении часто применяются долота сложных конфигураций, имеющие дополнительные поперечные лезвия, длина которых может составлять 25−30 % от длины основного. С этим связано то, что площадь разрушаемой породы будет иметь большие размеры, чем предполагалось, больше будут и силы сопротивления породы разрушению, а следовательно, меньше глубина внедрения лезвия долота при той же силе удара (на 25−30 %). Поэтому для долот сложной конфигурации вводят в формулу (3.58) поправочный коэффициент К1, учитывающий влияние длины и формы лезвий долота (К1 = 0,75–0,7).

Кроме того, глубина внедрения долота при повторных ударах его о породу будет уменьшаться в результате его затупления при износе лезвия. По данным практики, глубина внедрения долота в связи с притуплением лезвия долота снижается на 30−40 % и больше, что учитывается ещё одним коэффициентом К2 притупления до-

лота (К2 = 0,7–0,6).

Тогда в окончательном виде будем иметь:

138

Наконец, эту формулу можно упростить, заменив выражение tgα/2 + f буквой К. Тогда

3.2.4. Условия разрушения породы по всей площади дна скважины при ударном способе бурения

Для разрушения породы по всей площади дна скважины необходимо нанести целую серию ударов (рис. 3.32).

Рис. 3.32. Схема скалывания элементов породы при повторных ударах долота по забою и формирования ствола скважины цилиндрической формы:

I, II, III – порядок наносимых ударов

Чтобы скважина приобретала цилиндрическую форму, а эффективность разрушения была максимальной, следует после каждого удара поворачивать долото на строго определенный угол β. В этом случае порода будет разрушаться не только под торцом долота в пределах площади SК, но и за ее пределами на площади S′СК, S′′СК, под действием скалывающей силы ССК. Условием скалывания породы при этом бу-

дет: ССК > σСК (S′СК + S′′СК).

Объем скалывающейся породы будет зависеть, естественно, от свойств пород, в частности прочности на скалывание σСК, глубины внедрения h, суммарной площади SСК и величины скалывающей силыССК.

139