БТЖ и ФРГП на весну 16 года / БТЖ - лекции_2015 / СулакшинЧубик

новных механических свойств: упругости, хрупкости и пластичности, прочности или твердости и др.

Упругостью называется способность деформируемого тела восстанавливать первоначальную форму или объем после снятия нагрузки. Известно, что все твердые материалы в первом приближении подчиняются закону Гука, который является основой теории упругости: деформация упругого тела пропорциональна действующему усилию. Однако для горных пород эта зависимость оказывается более сложной из-за их сложного состава, пористости, влажности и других свойств, что приводит к получению нестабильных показателей и отклонениям от закона Гука, хотя минералы, слагающие породу, этому закону подчиняются. Упругость горных пород проявляется, прежде всего, в форме упругих деформаций, исчезающих после снятия нагрузки (обратимые деформации).

Поведение породы как твердого тела чаще всего иллюстрируют диаграммой деформаций, получаемой при вдавливании цилиндрического штампа с плоским торцом (рис. 2.3). В первый период нагружения (участок ОА) может быть упругая деформация по закону Гука. Такое поведение присуще большинству твердых горных пород. На участках АВ и ВС пропорциональность между нагрузкой и деформацией нарушается, т. е. происходит пластическая деформация. Углы наклона этих линий α, α1, α2 названы деформационными углами. Показателями упругих свойств горных пород служат: модуль упругости Е, коэффициент Пуассона μ, модуль сдвига G, модуль всестороннего (объемного) сжатия К.

Рис. 2.3. Диаграмма деформаций, получаемая при вдавливании цилиндрического штампа с плоским торцом (по Л.А. Шрейнеру)

Модуль упругости (или модуль Юнга) является коэффициентом пропорциональности между действующим нормальным напряжением σ и относительной деформацией δσ.

Для подавляющего большинства породообразующих минералов модуль упругости Юнга (по данным Л.А. Шрейнера [18]) изменяется в довольно узких пределах (табл. 2.4). Для горных пород величина модуля Юнга существенным образом зависит от вида деформации и величины приложенной нагрузки, что весьма важно. Заметное различие в модуле Юнга при различных видах деформаций имеет место

71

Между модулями упругости, определяемыми при статических ЕС и динамических ЕД нагрузках, для ряда пород установлена корреляционная связь [13]:

Значение модуля ЕС в данном случае определяется следующим образом (для песчаника с халцедоновым цементом), табл. 2.7:

EC 105 = 7,3,

или

10EC5 = 7,3,

откуда

EC = 7,3 105 = 730000 смкгс2 .

Модуль упругости пород существенно зависит от условий сжатия. Установлено, что при объемном сжатии модули упругости, как статический, так и динамический, возрастают по сравнению с их значениями, полученными при одноосном сжатии. Причем заметный рост наблюдается при всестороннем сжатии в пределах 500...1000 кгс/см2. Отмечено, что более интенсивно растет статический модуль упругости, увеличивающийся в 3 раза при всестороннем сжатии порядка (1000 кгс/см2), тогда как динамический модуль упругости увеличивается только в 1,5–1,6 раза. Объясняется это уплотнением породы, закрытием пор и увеличением площади контактов зерен, воспринимающих нагрузку при всестороннем сжатии образца. Установлено, что разница между ЕД и ЕС тем больше, чем более пористы породы.

Коэффициент Пуассона μ является коэффициентом пропорциональности между относительными продольными δ и поперечными δ' деформациями:

73

Коэффициент Пуассона для горных пород колеблется в широких пределах от 0,1 до 0,45, но в большинстве случаев имеет среднее значение около 0,25 (глины пластичные – 0,38…0,45; глины плотные – 0,25…0,35; глинистые сланцы –

0,10…0,20; известняки – 0,28…0,33; песчаники – 0,30…0,35; гранит – 0,26…0,29).

У разных пород этот показатель меняется по-разному, в зависимости от условий деформации. У одних возрастает, а у других уменьшается.

Модуль сдвига G является коэффициентом пропорциональности между касательным напряжением τ и соответствующей деформацией сдвига δτ:

Модуль сдвига G может быть вычислен, если известны модуль упругости Е и коэффициент Пуассона μ, с помощью выражения

Значения модуля сдвига для разных пород различны. По данным П.М. Цимбаревича, модуль сдвига для известняков составляет (2,5…6,5)·103 кгс/см2, для мрамора 1,5·103 кгс/см2, для кварцита 12,8·103 кгс/см2.

Модуль всестороннего сжатия К характеризует в случае объемного сжатия связь между напряжением σ и относительным изменением объема V/V. Для идеально упругих тел модуль объемного сжатия может быть вычислен с помощью выражений [13]:

Все модули имеют размерность Н/м2 или внесистемную кгс/см2. Коэффициент Пуаcсона является величиной безразмерной.

Хрупкость и пластичность горных пород. Поведение горных пород при де-

формациях, как указывалось ранее, может быть различным. В одних случаях под действием приложенных сил порода будет менять только свою форму и объем без разрыва сплошности, т. е. деформироваться пластически, в других – порода разрушается на отдельные элементы без заметной пластической деформации (без поглощения механической энергии в необратимой форме). В соответствии с таким поведением горных пород выделяются их важные свойства: пластичность и хрупкость.

Пластичностью называется способность породы получать остаточные деформации или поглощать, не разрушаясь, механическую энергию в необратимой форме. Синонимом этого понятия является вязкость.

Пластическая деформация в твердых горных породах объясняется двумя основными процессами: межкристаллическим скольжением и пластическим течением внутри минеральных зерен. Проявление и преобладание того или иного процесса зависят от многих факторов, к числу которых относятся: сила связи между зернами минералов или кристаллитами, пластические свойства кристаллов минералов, спайность, свойства цементирующего материала и др.

Хрупкостью называется способность горной породы разрушаться без заметного поглощения механической энергии в необратимой форме, т. е. без заметной пластической деформации.

74

Большинство горных пород проявляют хрупкие свойства, и только при условии всестороннего сжатия возникают пластические деформации. При этом может наступить пластическое течение, когда деформация нарастает со временем без увеличения нагрузки. Деформационный угол α на диаграмме в таком случае будет равен нулю (см. рис. 2.3). Нагрузку, при которой упругие деформации переходят в пластическую, принимают за условный предел текучести. Если при нагружении образца после упругой деформации наступает пластическая деформация, а затем хрупкое разрушение, порода относится к группе хрупкопластических тел. Наконец, если порода при нагружении с самого начала деформируется пластически или течет, то она относится к пластическим или вязким породам.

Установить точной границы между хрупкими и пластичными породами практически очень трудно, так как проявление этих свойств зависит и от характера приложенной силы, например от скорости нагружения. Одна и та же порода может вести себя и как хрупкое, и как пластичное тело. Действительно, при достаточно быстрых деформациях у большинства пород разрушение наступает раньше, чем текучесть, т. е. хрупкое разрушение наступает раньше, чем проявляются остаточные деформации. В этом случае порода будет проявлять свойства хрупкого материала. Так, например, каменная соль, вар, стекло, мрамор и другие материалы при быстром действии нагрузки (при ударе) раскалываются как хрупкие тела. При медленном нагружении у них же проявляются пластические свойства: вар растекается или приобретает форму сосуда, в котором он медленно прессуется. Также может течь каменная соль, которую можно выдавить через отверстие любой формы. Палочка из стекла, положенная на две опоры, в течение времени прогнется и станет изогнутой. Также ведут себя породы в природе в процессе складкообразования.

Проявление свойств, согласно теории твердого тела, можно характеризовать следующим уравнением:

где σ – напряжение; Е – модуль упругости; х – величина деформации; η – коэффициент вязкости; t – время действия нагрузки. В случае быстрого увеличения нагрузки время t имеет небольшое значение и второй член уравнения быстро возрастает. Напряжение σ быстро приближается к пределу прочности или превышает его. Происходит хрупкая деформация. При медленном возрастании прилагаемой нагрузки напряжение σ увеличивается постепенно, и происходит пластическая деформация. Это явление имеет существенное значение для процессов бурения. При медленном приложении нагрузки в породе могут развиваться остаточные деформации и она не будет разрушаться. При быстром приложении нагрузки порода разрушается, проявляются хрупкие деформации, объем разрушенной породы увеличивается. Таким образом, с ростом скорости нагружения уменьшается пластичность пород, но возрастают твердость и предел текучести (рис. 2.4), и порода из хрупкопластичной переходит в хрупкую.

75

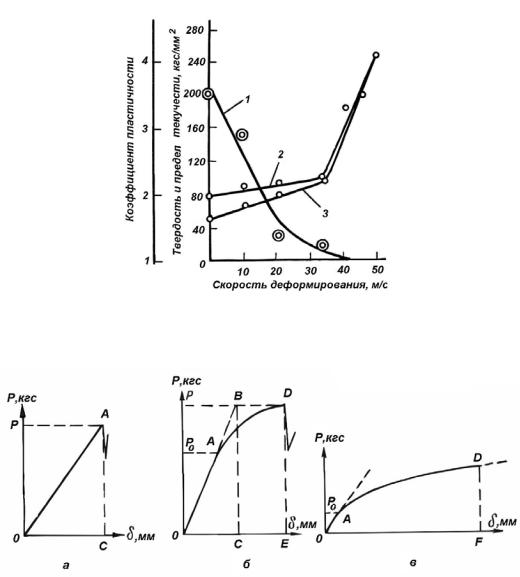
Рис. 2.4. Диаграмма изменений свойств пород в зависимости от скорости деформирования при внедрении штампа диаметром 10 мм

(по данным Н.Н. Павловой и Л.А. Шрейнера):

1 – коэффициент пластичности; 2 – твердость; 3 – предел текучести

Рис. 2.5. Графики деформаций пород (по Л.А. Шрейнеру):

а– хрупких (кварцит); б – пластично-хрупких (мрамор);

в– высокопластичных (каменная соль) и сильнопористых

На рис. 2.5 приводятся графики, характеризующие поведение горных пород при вдавливании штампа по методу Л.А. Шрейнера. График деформации хрупкой породы (кварцита) показывает (рис. 2.5, а), что до момента хрупкого разрушения в точке А под торцом штампа имела место упругая деформация. На рис. 2.5, б показан график деформации пластично-хрупкой породы (мрамора). До точки А была упругая деформация и далее – пластическая до точки D, в которой порода хрупко разрушается. При вдавливании штампа в типично пластичную породу (рис. 2.5, в) происходит пластическая деформация без хрупкого разрушения.

Показателем пластических свойств пород могут служить предел текучести или коэффициент пластичности. Предел текучести РТ, характеризующий пластичнохрупкие породы, определяется отношением нагрузки Р0 соответствующей точке

76

перехода от упругой деформации к пластической, к площади торца вдавливаемого штампа S и оценивается внесистемной единицей кгс/см2.

Коэффициент пластичности КП (по Л.А. Шрейнеру и О. П. Петровой) характеризуется отношением работы, затраченной на упругую и пластическую деформацию А0 (до разрушения породы), к работе, затраченной на упругие деформации АУ, за вычетом работы, затраченной на деформацию штампа АШ:

Для пород высокопластичных коэффициент пластичности принимается равным бесконечности. Для пород плотных и с незначительной пористостью коэффициент пластичности достигает 7. У пористых пород коэффициент пластичности увеличивается за счет дополнительной остаточной деформации, связанной с уплотнением породы, что следует учитывать при оценке этого показателя.

Показателем хрупкости горных пород Л.И. Барон и В.М. Курбатов предложили считать коэффициент хрупкости КХ, представляющий собой отношение работы, затрачиваемой на чисто упругую АУ, к общей работе, затраченной на деформацию и разрушение породы А0, что является величиной, обратной коэффициенту пластичности:

Прочность горных пород

Понятие «прочность» может быть определено как способность твердого тела сопротивляться силам, стремящимся разрушить связь между элементами (частицами, из которых состоит это тело). Прочность горных пород зависит от характера, силы связи или сцепления и силы внутреннего трения между частицами, слагающи-

77

ми породу, что обусловливается рассмотренными ранее факторами, а также от условий и способа определения этого свойства.

У горных пород силы сцепления С возникают при непосредственном контакте зерен (кристаллов разных минералов или их обломков) или за счет цементирующей массы, заполняющей промежутки между зернами или обломками. Поэтому у горных пород можно выделить силы сцепления: внутри зерен (кристаллов или их обломков) СВЗ, между зернами СМЗ, между зернами и цементом СЗЦ и внутри цемента СВЦ. Обычно связь внутри зерен наиболее совершенная и прочная, нежели между зернами и цементом. Редко встречается обратная картина.

Разрушение породы можно представить себе как перемещение одного участка относительно другого, что связано с проявлением сил трения, создающих дополнительное сопротивление силам, вызывающим разрушение породы. Действительно, разрушение образца породы или некоторого объема происходит при возрастании одного из главных напряжений, вызывающих деформацию образца. Так, например, если в условиях трехосного сжатия образца одно из главных напряжений σ1 окажется больше двух других σ2 и σ3, произойдет сдвиг одной части относительно другой в плоскости развития максимальных тангенциальных напряжений τ, расположенной под углом β к оси большего из главных напряжений (см. рис. 2.2). Как было выяснено ранее, этот угол теоретически равен 45°. Для горных пород он обычно имеет близкие к этому значения, отличающиеся в большую или меньшую сторону. Таким образом, потеря прочности при сжатии характеризуется сдвигом некоторых элементов породы, который наступает в тот момент, когда касательные напряжения превысят некоторое предельное значение сил сопротивления породы сдвигу.

Условие прочности твердого тела впервые было определено Кулоном и затем подтверждено экспериментально: момент перехода от равновесия к разрушению, то есть предельное состояние образца при деформации, выражается зависимостью между сопротивлением породы сдвигу, или тангенциальным напряжением τ, и нормальным напряжением σН к поверхности сдвига:

где kf – коэффициент трения; С – сила сцепления зерен.

Это выражение представляет собой уравнение прямой линии, отсекающей на

Первый член этого уравнения tgϕσH рассматривается как сопротивление сил трения F = kfσН сдвигу элементов породы, возникающих между частицами, слагающими эту породу. По аналогии с законом трения kf определяется как коэффициент внутреннего трения породы, а φ является «углом внутреннего трения». Величина С была принята за показатель сцепления, определяемого силами связи между частицами, слагающими породу. Таким образом, величины φ и С отражают в первом приближении количественные характеристики прочности пород.

Рассмотренное условие прочности пород, выраженное уравнением прямой линии (2.23), в механике горных пород названо условием предельного равновесия. Это условие может быть выражено посредством главных напряжений σ1 и σ2, если σ2 = σ3, a σ1< σ2, с использованием кругов Мора (рис. 2.6). По оси абсцисс откладываются значения главных напряжений σ1 и σ2, а на их разности строится окруж-

78

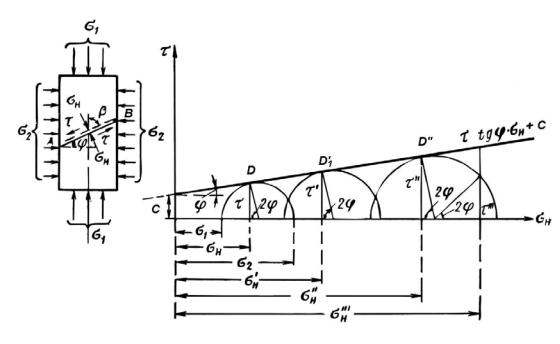
ность, диаметр которой d = σ1 – σ2. Ординаты и абсциссы любой точки этого круга соответствуют значениям στ и τ для различно расположенных площадок в данной точке. Так, для площадки АВ, расположенной под углом φ к плоскости, на которую действует большее главное напряжение σ1, значениями τ и σН являются координаты точки D. Если для ряда горизонтальных напряжений этой же породы установлены значения нормальных предельных напряжений σН, σН′, σН′′, σН′′′ и т. д., при которых происходит разрушение породы, то строится серия кругов напряжений (рис. 2.6), общая касательная к которым будет являться графическим изображением условия предельного равновесия. Угол наклона этой линии будет характеризовать угол внутреннего трения φ данной породы, а отрезок, отсекаемый этой линией на оси ординат, – показатель сцепления С.

Рис. 2.6. Графическое изображение условия предельного равновесия с помощью кругов Мора

Таким образом, сопротивление горных пород тангенциальным нагрузкам (прочность на сдвиг) определяется, прежде всего, величиной сцепления С и зависит от коэффициента трения движения перемещающихся элементов (участков) породы и нормального напряжения, т. е. от силы трения:

Пользуясь диаграммой Мора и главным напряжением σ1 и σ2 = σ3, сцепление можно выразить уравнением

Силы сцепления между зернами возрастают при действии на породу давления, особенно в течение длительного времени. Это объясняется уменьшением расстояний между зернами, что приводит к увеличению сил взаимодействия между частицами. При растяжении происходит обратная картина, поэтому прочность пород при сжатии всегда больше. Поэтому силы сцепления, характеризующие сопротивляе-

79

мость пород разрушению при различных видах деформации (сжатие, растяжение, срез или скалывание), имеют, соответственно, различные значения.

Используя диаграммы Мора, Фрелих [19] нашел зависимости между сцеплением С, прочностью на сжатие σСЖ и растяжение σР и углом внутреннего трения породы , имеющие следующий вид:

где ССЖ, и СР – соответственно сцепление пород при сжатии и растяжении. Многие исследователи считают, что величина сцепления мало отличается от прочности на разрыв (в пределах 1–6 %). Поэтому для практических расчетов принимают СР ≈ σР.

Коэффициент трения Kf, определяемый как тангенс угла внутреннего трения φ, для разных пород имеет различные значения. При этом следует различать коэффициенты трения покоя и движения. В табл. 2.9, 2.10 приводятся некоторые значения коэффициентов трения породы о породу и породы о другие материалы по данным различных авторов.

80