4.2. Построение а.Ф.Х. Линейной части. Его характер можно определить по его графику, показанному на рисунке 15. График колебательного процесса получен средствами анализа программы SyAn.

Рис. 14 – САУ с нелинейностью

Определим критический коэффициент системы К_кр.

В характеристическом уравнении замкнутой астатической САУ свободный член равен К_раз.

Для определения К_кр по критерию Найквиста необходимо определить величину запаса устойчивости по модулю а: a=1/7,4=0,14.

Тогда критический коэффициент усиления разомкнутой системы рассчитывается по формуле:

К_кр=а К_раз=1,26. Так как К_кр < К_раз,

то рассматриваемая система неустойчива (–аналитический расчёт подтвердил).

Критерий Найквиста предполагает построение годографа на комплексной плоскости. Для построения годографа из характеристического уравнения замкнутой системы путем подстановки p=iω получаем аналитическое выражение вектора:

Выделяем мнимую и действительную части:

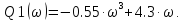
Рис. 5.1 Годограф Найквиста

Из рис 5.1 видно, что годограф Найквиста последовательно обходит в положительном направлении 4 квадранта, следовательно, нескорректированная САУ устойчивая. Для достоверности определим критический коэффициент усиления разомкнутой К_кр при котором замкнутая САУ находится на границе устойчивости. Условием нахождения системы на границе устойчивости является прохождение годографа Найквиста через начало координат. В этом случае существует значение ω, при котором

т.е. ,

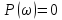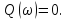
Для нахождения К_кр решим систему уравнений:

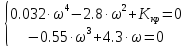
Из уравнения (2) найдем частоту ω:

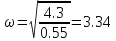
Подставим найденную частоту в уравнение (1) и найдем К_кр:

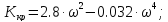
Так как К_кр > К_раз, то рассматриваемая нескорректированная система устойчива.

6. D-разбиение по параметру К_у.

Для построения кривой D-разбиения по параметру К_д характеристическое уравнение замкнутой САУ:

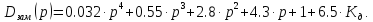
Представляется в виде:

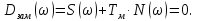
где S(ω) - полином, не содержащий параметр К_д; N(ω) - полином в который линейно входит параметр К_д, по которому выделяется область устойчивости.

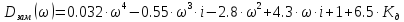
Определим параметр К_д:

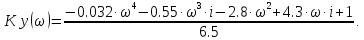
Выделим действительную и мнимую часть:

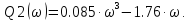
Строим на комплексной плоскости К_у кривую и штрихуем одинарной штриховкой для определения претендента на область устойчивости. Кривая D-разбиения по 1-му параметру штрихуется одинарной штриховкой слева, если двигаться по границе устойчивости в направлении возрастания ω от -∞ до ∞. Претендентом на область устойчивости является та, которая имеет наименьшее количество правых корней.

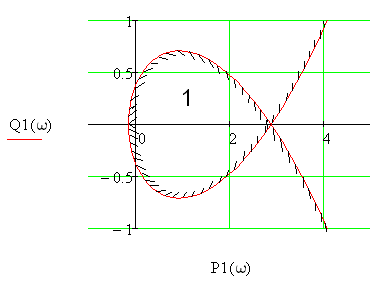
Рис. 6.1 D-разбиение

Область 1 - вероятный претендент на устойчивость. Проверим ее на устойчивость по Гурвицу, взяв точку К_д = 1.

Тогда характеристическое уравнение примет вид:

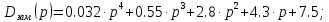
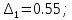
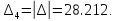
Область 1 является областью устойчивости, т. к. определители Δ₁, Δ₂, Δ₃, Δ₄ > 0.

Взяв значение параметра К_д = 1.9 для начальных данных, мы получим следующее характеристическое уравнение.

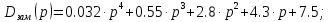
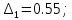
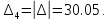
Исходя из условий Гурвица можем утверждать о устойчивости системы в данной точке. Лишний раз убедились в устойчивости системы.

7. Определение параметров корректирующего устройства.

Для t_рег = 0.15 ε_ст = 0.015 и σ = 20 % по номограммам Солодовникова определим :

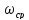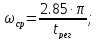
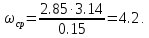
Для САУ с такой частотой среза рекомендуется следующие средние показатели устойчивости: φ_зап = 45, H_м = 16 дБ, -H_м = 14 дБ. Для того чтобы обеспечить необходимую скоростную ошибку коэффициент K_тр должен быть равным:

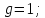
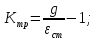
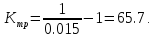
По требуемым значениям построим логарифмические частотные характеристики передаточных функций. Передаточная функция нескорректированной САУ:

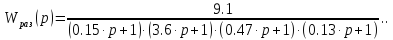
Передаточная функция желаемой САУ:

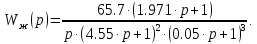
Передаточная функция последовательного корректирующего устройства находится графическим способом. Графики нескорректированной, скорректированной систем и корректирующего устройства представлены на рис 7,1..

Рис. 7.1 ЛАХ нескорректированной системы L₀, желаемой разомкнутой системы L_ж и последовательного корректирующего устройства L_ку.

Передаточная функция последовательного корректирующего устройства для САУ:

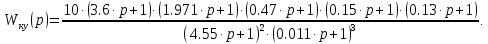
При схемной реализации корректирующей цепи воспользуемся таблицами RC-цепей. Здесь возможен вариант, когда цепь коррекции является совокупность ряда табличных цепей, т.е. корректирующая цепь составляется из последовательных каскадов, моделирующих типовые передаточные функции. Разобьем передаточную функцию корректирующего устройства на несколько простых звеньев. Задаваясь одним параметром схемы, находим через соответствующие формулы параметры всей схемы.

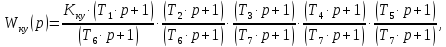
где

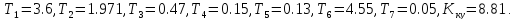
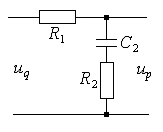
Рис. 7.2. Схема корректирующего звена

Первое звено соберем по схеме показанной на рис. 7.2.

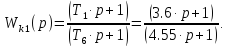
Возьмем:

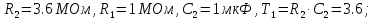
Второе звено соберем по схеме показанной на рис. 7.2.

Возьмем:

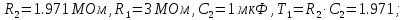
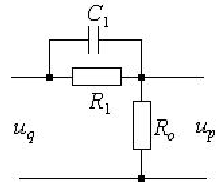
Рис. 7.2. Схема корректирующего звена

Третье звено соберем по схеме показанной на рис. 7.3.

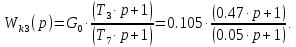
Возьмем:

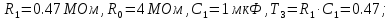
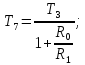
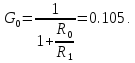
Четвертое звено соберем по схеме показанной на рис. 7.3.

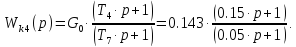
Возьмем:

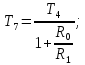
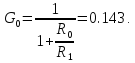
Пятое звено соберем по схеме показанной на рис. 7.3.

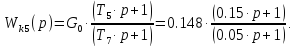
Возьмем: