IV. Векторная алгебра § 1. Векторы

Величина, которая полностью определяется своим числовым значением, называется скалярной или скаляром (термин ввел У. Гамильтон в 1843 г.). Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора, который ранее уже использовался в примерах.

Вектор – это направленный отрезок. Если А – начало вектора, а В – его конец, то вектор обозначается символом или. Вектор,называетсяпротивоположным вектору . Вектор противоположный вектору_, обозначается ().

Длиной вектора называется длина отрезкаи обозначается. Вектор, длина которого равна нулю, называетсянулевым вектором и обозначается (или 0, когда нет сомнений в понимании обозначения). Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным и обозначается через. Единичный вектор, направление которого совпадает с направлением вектора, называетсяортом вектора . Векторыиназываютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых.

Два вектора иназываютсяравными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку O пространства, то есть векторы определены с точностью до параллельного переноса.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

§ 2. Линейные операции над векторами

Под линейными операциями над векторами понимают операции сложения векторов и умножение их на число.

Геометрическая интерпретация. Пусть идва произвольных вектора. Возьмем произвольную точкуO и построим из нее вектор . От точкиA отложим вектор . Вектор, соединяющий начало первого вектора с концом второго, называется суммой векторови:(рис.IV.1).

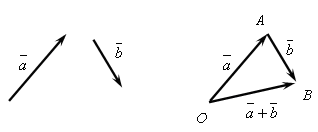
Рис. IV.1

Это правило сложения векторов называется правилом треугольника. Аналогично происходит сложение нескольких векторов (рис IV.2):

Рис. IV.2

Под разностью векторов ипонимается вектор. На практике вектораиоткладывают из одной точки, концы соединяют и вектор имеет направление «к концу вектора».

Отметим, что в параллелограмме (рис. IV.3), построенном на векторах и, одна направленная диагональ является суммой векторови, а другая разностью.

Рис. IV.3

Произведением вектора на скаляр (число)λ, , называется вектор, который имеет длину вектора, умноженную наλ, а направление совпадает с направлением вектора , если, и противоположно направлению вектора, если.

Линейные операции над векторами обладают следующими свойствами:

1) ;	3) ;
2) ;	4) ;
5) , .

Эти свойства позволяют проводить преобразования над векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.