§ 3.2Анализ движения механизмов

3.2.1Режимы движения механизмов

Полное время движения механизма– промежуток времени от момента начала движения до момента его окончания.

Т.к. закон движения всех звеньев механизма зависит от закона движения ведущего звена, то полное время определяется по промежутку времени движения ведущего звена.

Полное время состоит из трех частей

1. Время разбега t_р– время, при котором происходит возрастание угловой скорости ведущего звена от нулевого значения до среднего. Оно характеризует нормальную рабочую скорость ведущего звена (начало работы механизма).

2. Время установившегося движения t_ус.дв.–время, при котором происходит колебание скорости ведущего звена около среднего значения, периодически при этом повторяющейся (работа механизма).

3. Время выбега t_в– время, при котором происходит убывание скорости ведущего звена от среднего значения до нулевого (остановка механизма).

Итак, полное время является суммой t_р, t_ус.двиt_в, т.е.

t_полн.= t_р+ t_ус.дв + t_в= (с). (3.57)

Зависимость угловой скорости ведущего звена от времени отображается зависимостью ω = ω(t), называемойтахограммой механизма (рисунок 3.15).

Цикл установившегося движения– промежуток времени установившегося движения, по истечении которого положение, скорость и ускорение ведущего звена принимают первоначальные значения.

На рисунке 3.15 время установившегося движения имеет четыре цикла, поэтому время t_ус.двбудет вычисляться по формуле

t_ус.дв= kt_ц, (3.58)

где k– число циклов,t_ц– время цикла.

ω

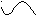
ω_max ω_ср ω_min

t

t_ц t_ц t_ц t_ц

t_р t_ус.дв t_в

t_полн

Рисунок 3.15 - Тахограмма механизма

Продолжительность времени t_р, времениt_ус.дв и времениt_взависит от соотношения между действующими силами, массами и кинематическими параметрами механизма и если эти соотношения известны, то всегда можно определитьt_р, t_ус.двиt_в. Полное время установившегося движения может состоять из любого числа циклов движения и зависит от того, сколько долго необходимо поддерживать рабочий режим движения механизма со средней угловой скоростью.

Периодическое движение механизма– такое, при котором механизм обладает постоянными циклами движения, причем в течение каждого цикла движение происходит по одному и тому же закону. На рисунке 3.15 показано, что механизм имеет периодическое движение на участке времениt_ус.дв. Цикл может соответствовать одному или нескольким оборотам ведущего вала.

Рассмотрим с точки зрения динамики характеристику разбега, установившегося движения и выбега. Для этого запишем уравнение кинетической энергии

А_дв.с.-А_с.с.=, (3.59)

где А_дв.с - работа движущих сил,А_с.с.,Т = mυ²/2- кинетическая энергия механизма,υ- скорость в конце движения,υ₀ - скорость в начале движения.

Для времени разбега, необходимо, чтобы скорость в конце движения была больше скорости в начале движения, т.е. υ > υ₀. А это влечет за собой требование, чтобы работа движущих сил была больше работы сил сопротивления, а именно:

А_дв.с.>А_с.с;

для времени установившегося движения начальная скорость равна величине конечной скорости υ = υ₀, поэтому работы также равны друг другу:

А_дв.с.= А_с.с ;

для времени выбега υ < υ₀и поэтому

А_дв.с.<А_с.с.

Следовательно, правая часть уравнения (3.59) для каждого движения примет вид:

для времени разбега

> 0;

для времени установившегося движения

= 0; (3.60)

для времени выбега

< 0.

Из уравнений (3.60) видно, что за время разбегапроисходитприращениекинетической энергии.Во время установившегося движения приращение кинетической энергии равно нулю. Завремя выбегапроисходитотдача кинетической энергии, накопленной за время разбега.