II класса 1 вида

Исходные данныедля расчета:

ℓ_АВ, ℓ_ВС, ℓ_ВЕ = ℓ_СЕ - длины звеньев вм;υ_А, υ_С - скорости внешних шарниров (направление и величина) вм/с;а_А, а_С - ускорения внешних шарниров (направление и величина) вм/с².

Определить:υ_В, а_В - направление и величина скорости и ускорения внутреннего шарнира;ω₂, ω₃ - угловые скорости звеньев;ξ₂, ξ₃ - угловые ускорения звеньев;υ_Е, а_Е - скорость и ускорение точкиЕ.

Общие сведения.В точкеВсоединены 2 звена. Поэтому будут две точкиВ:В₂, принадлежащая второму звену, иВ₃, принадлежащая третьему.Еслизвенья соединены во вращательную кинематическую пару, то линейные скорости и ускорения будут равны, а угловые нет, т.е.

υ_В2 = υ_В3, а _В2 = а _В3, ω₂  ω₃, ξ₂  ξ₃.

Решение.Рассчитывается масштабный коэффициент плана скоростей

μ_υ = υ_А/[Р_υа] = (м/с), (2.30)

причем отрезок [Р_υа]выбирается произвольно.

Затем считается чертежная величина вектора скорости точки С

[Р_υс] = υ_С /μ_υ = (мм). (2.31)

Построение плана скоростей. На свободном поле чертежа выбирается точка полюса Р_υ. Из нее строятся заданные или заранее определенные отрезки скоростей [Р_υа] и [Р_υс] (рисунок 2.6). Для определения скорости точки В движение этой точки раскладывается на переносное поступательное со скоростями точек А и С и относительное вращательное вокруг этих же точек. Тогда, воспользовавшись сложением скоростей, векторные уравнения будут иметь вид:

υ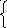_В = υ_А+ υ_ВА  АВ;

υ_В = υ_С + υ_ВС  ВС. (2.32)

В(В₂,В₃) а υ_А Р_υ

υ_В υ_С

2 3 ω₃ с

υ_ВА υ_Е

А Е С е

1 ω₂ 4 в υ_ВС

υ_А υ_С

Рисунок 2.6 - Схема структурной группы IIкласса 1 вида

и ее план скоростей

Направления относительных скоростей известны по направлению: υ_ВА  АВ, υ_ВС  ВС. Величины этих скоростей будут находиться из построения плана скоростей. Для этого из точки а на плане скоростей проводится линия действия скорости υ_ВА, перпендикулярная звену АВ, а из точки в проводится линия действия вектора скорости υ_ВС, перпендикулярная звену ВС. На пересечении получается искомая точка в.

Точка е на плане скоростей определяется по правилу подобия:

1. если на схеме механизма имеется жесткий треугольник (ΔВСЕ), то на плане скоростей (ускорений) будет подобный треугольник (Δвсе), причем порядок букв на схеме механизма будет совпадать с порядком букв на плане скоростей или ускорений (обход контура);

2. если точка находится на звене и делит его на пропорциональные отрезки, то данная точка на плане скоростей(ускорений) будет находиться на соответствующем векторе и делить его на равнозначные пропорциональные отрезки;

3. если точка находится на продолжении звена, то на плане скоростей (ускорений) она будет находиться на продолжении соответствующего вектора, причем порядок букв на схеме механизма будет совпадать с порядком букв на плане скоростей или ускорений.

Воспользуемся п.1 из правила подобия. Так как по заданию ℓ_ВЕ = ℓ_СЕ, то и отрезки ве = се. Длина этих отрезков определится из пропорции

ℓ_ВЕ/ℓ_ВС=ве/вс. (2.33)

Теперь из точек в и с проводятся дуги до их пересечения, равные этим отрезкам. Получается искомая точка в.

Определяются действительные значения всех найденных векторов скоростей:

υ_В = [Р_υв]μ_υ =

υ_Е = [Р_υе]μ_υ = (м/с).

υ_ВА = [ав]μ _υ=

υ_ВС = [вс]μ_υ =

Отрезки замеряются на плане скоростей в мми умножаются на масштабный коэффициент плана скоростей.

После определения линейных скоростей определяются угловые скорости:

ω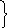₂ = υ²_ВА/ℓ_АВ = (с^-1),

ω₃ = υ²_ВС/ℓ_ВС = (2.34)

а затем и их направления.

Определим направление угловой скорости ω₂. Для этого вектор линейной скорости υ_ВА мысленно переносим во внутренний шарнир на схеме механизма, т.е. в точку В, и вращаем точку В относительно точки А (точку А считаем неподвижной). Аналогично определяем направление ω₃.

Построение плана ускорений. Рассчитываем масштабный коэффициент плана ускорений:

μ_а = а_А/[Р_аа] = (^м/с2/_мм). (2.35)

Затем высчитываем чертежную величину вектора ускорения точки С:

[Р_ас] = а_С/µ_а = (мм). (2.36)

На свободном поле чертежа произвольно выбирается точка полюса Р_а. Из нее проводятся ранее определенные отрезки [Р_аа] и [Р_ас] (рисунок 2.7).

Для определения ускорения внутреннего шарнира (точки В) рассматриваем ее сложное движение. Сложное движение состоит из переносного поступательного с ускорениямиа_Аи а_С, и относительного вращательного вокруг точекАиС. Тогда векторные уравнения для определения ускорения точкиВбудут следующие:

а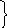_В = а_А + аⁿ_ВААВ + а^τ_ВААВ

а_В = а_С + аⁿ_ВСВС + а^τ_ВСВС(2.37)

В а а_А Р_а

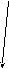
аⁿ_ВА

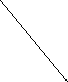
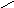
2 3 n_ВА а_С

ξ ₂ ξ ₃ а_ВА а_В с

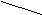
А Е аⁿ_ВС

а_А С а^τ_ВА e n_ВС

1 а_С 4 а^τ_ВС

в

Рисунок 2.7 - Схема структурной группы II класса 1 вида

и ее план ускорений

В уравнении (2.37) известны направления всех векторов: нормальные ускорения направляются параллельно звеньям к центру вращения, а тангенциальные - перпендикулярно этим же звеньям. Величины нормальных ускорений находятся по формулам в (м/с²):

а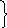ⁿ_ВА= υ²_ВА/ℓ_АВ =

аⁿ_ВС = υ²_ВС/ℓ_ВС = (2.38)

Вычисляем чертежные значения нормальных ускорений в мм:

(2.39)

Тангенциальные ускорения определяются построением плана ускорений.

Из точки ана плане ускорений откладываем вектор АВи направляем его к точкеА. Затем из точкиn_ВАпроводим линию действия тангенциального ускоренияа^τ_ВААВ.Через точкуспроводим вектор ВСи направляем его к точке С, а из точкиn_ВСпроводим линию действия тангенциального ускоренияа^τ_ВС  ВС. Пересечение этих линий даст искомую точкуви определит длины векторов тангенциальных ускорений. Точкуенайдем по п.1правила подобия. Для этого составим пропорцию:ℓ_ВС/ℓ_ВЕ = вс/веи строим аналогично скорости. Действительные значения ускорений определяются по формулам:

а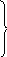_В= [Р_ав] μ_а = (м/с²);

а_Е = [Р_ае] μ_а = (м/с²);

а^τ_ВА = [n_ВАв] μ_а = (м/с²);(2.40)

а^τ_ВС = [n_ВСв] μ_а = (м/с²).

Величина угловых ускорений определяется по формулам:

ξ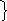₂ = а^τ _ВА/ℓ_АВ = (с^-2);

ξ₃ = а^τ _ВС/ℓ_ВС = (с^-2).(2.41)

Для определения направленияугловых ускоренийнеобходимо векторы этих ускорений мысленно приложить во внутренний шарнир и поворачивать звенья относительно точекА и С(рисунок 2.7).

Задача 2. Кинематический анализ структурной группы