Казунина Г. А

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

U ( ) Re S( )

f (t) cos tdt

f (t) cos tdt.

..pdf

Скачиваний:

Добавлен:

16.03.2016

Размер:

2.06 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

	i	k	i	k
	i		i
1 e		2	e	2

k			2i
k			2i

sin k2 . k

Для спектральной плотности получаем

S( k )

sin( k / 2)

Амплитудный спектр

S( k )

можно

построить, задавая

номера гармоник:

k 0,1, 2,

S k

и нанося

их

на

диаграмму

( k ;

S( k )

). При этом получим

дискретный

(линейчатый)

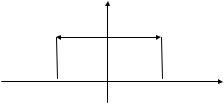
спектр (рис. 1.8).

-3

-1 0 1

Рис. 1.8

Следствием условия c k ck является то, что спектральная плотность S( k ) симметрична относительно оси ординат.

Аналогично вычисляя arg S( k ) для различных гармоник, получим фазовый спектр (рис. 1.9).

( k ) arg S( k )

				k
1	2	4	5	k

		Рис. 1.9

2. ПРЕОБРАЗОВАНИЯ ФУРЬЕ

2.1. ИНТЕГРАЛ ФУРЬЕ

Рассмотрим функцию f (x) , удовлетворяющую следующим условиям:

1) f (x), f (x) – определены на интервале ( ; ) , являются непрерывными или кусочно-непрерывными (могут иметь конечное число точек разрыва 1-го рода);

2) f (t) является абсолютно интегрируемой, то есть несоб-


ственный интеграл		f (t)	dt сходится.

Функция f (t)	не является периодической, но на любом ко-

нечном симметричном интервале ( l,l) может быть представлена рядом Фурье:

k t

f (t)

f (t)e

l .

2l l

Вводя

(k 1)

перепишем разложение f (t) в

следующем виде:

k t

f (t)

f (t)e

dt e

k t

k .

f (t)e

dt e

k 2

Переходя к пределу при условии (l ; k d ) , получим представление функции f (t) несобственным интегралом, который называют интегралом Фурье:

	1
f (t)		f (t)e
f (t)		f (t)e
	2
	2

i t dt ei t d .

Вводя специальное обозначение для внутреннего интеграла:

S ( )	1		i t dt ,
	1	f (t)e		(2.1)
		f (t)e		(2.1)
	2

перепишем интеграл Фурье в виде

f (t) S( )ei t d .				(2.2)

Соотношения (2.1) и (2.2) называют прямым и обратным преобразованиями Фурье соответственно. Прямое преобразование Фурье S( ) называют также спектральной плотностью. Эта функция дает анализ частотного состава временного сигнала f (t) . В отличие от спектральной плотности периодической функции функция S( ) является непрерывной и служит огибающей для соответствующего дискретного спектра.

Пример 2.1. Найти спектральную плотность одиночного прямоугольного импульса (рис. 2.1):

f(t)	1
	1		0,
			0,

			f (t) 1,


–l/2	0 l/2	t	0,
–l/2	0 l/2	t

tl / 2,

l / 2 t l / 2, t l / 2.

Рис. 2.1

l / 2

S ( )

f (t)e i t dt

e i t dt

2 l / 2

l / 2

e i t

l / 2

sin

1 e

S( )

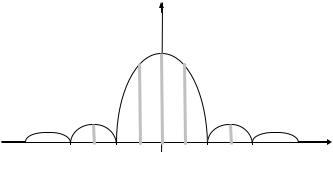
График функции S( ) огибает

дискретный спектр частот

прямоугольного

периодиче-

ского импульса (рис. 2.2).

Рис. 2.2

2.2. КОСИНУС- И СИНУС-ПРЕОБРАЗОВАНИЯ ФУРЬЕ

В общем случае спектральная плотность S( ) является функцией комплексной переменной:

S( ) U ( ) iV ( ) ;

		1
S ( )		1		f (t)e i t dt
S ( )				f (t)e i t dt
			2
	1
	1	f (t) cos tdt i			f (t) sin tdt

						;

	2

U ( ) Re S( ); V ( ) Im S( ).

Если функция f (t) является четной, то мнимая часть V ( ) 0 (как интеграл от нечетной функции на симметричном интервале). Спектральная плотность в этом случае имеет вид

Полученное преобразование называют косинус-

преобразованием Фурье.

Если функция f (t) является нечетной, то вещественная часть U ( ) 0 и спектральная плотность имеет вид

	1
V ( ) Im S( )		f (t)sin tdt,

		0

который называют синус-преобразованием Фурье.

Обратные преобразования задаются следующими соотношениями:


f (t) U ( ) cos td ;	f (t) V ( )sin td .
0	0

Рассмотрим примеры нахождения прямых и обратных преобразований Фурье.

									0,				t 0,
Пример 2.2. f (t) e t , t 0.

				1
	S( )			1			f (t)e						i t dt				1			e ( i )t dt
	S( )			2			f (t)e						i t dt				2			e ( i )t dt
				2													2			0
							1						1		e ( i )t
							1						1		e ( i )t
							2					i										0
																						0
					1						1				1				i					;
																								;
					2				i							2		2 2
Re S( ) U ( )			1											; Im S( ) V ( )											1			.
Re S( ) U ( )								2 2						; Im S( ) V ( )											2		2 2	.
				2				2 2																	2		2 2
При вычислении										интеграла							использовали									соотношение
e ( i )t	e t 0 при t .
e ( i )t	e t 0 при t .
Находим спектральные характеристики функции:
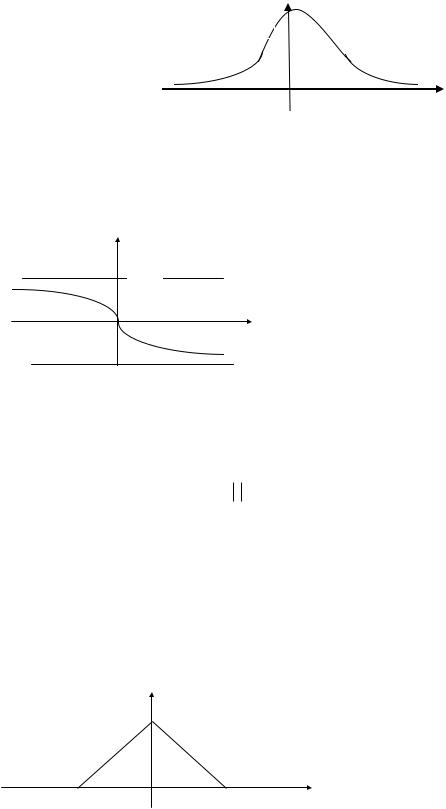
1) амплитудный спектр (рис. 2.3)
																			1		1
		S( )				U 2 ( ) V 2 ( )																				;



																			2				2 2
																			2				2 2

S( )

Рис. 2.3

2) фазовый спектр (рис. 2.4):

Рис. 2.4

( ) arg S( ) arctg .

Пример 2.3. f (t) e t .

В силу четности функции находим косинус-преобразование Фурье:

	1		1		1	1
S( ) U ( ) 2 Re		e t e i t dt		Re				.
S( ) U ( ) 2 Re		e t e i t dt		Re				.
	2 0				i		2 2
	2 0				i		2 2

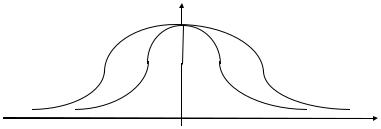
Пример 2.4. График функции представлен на рис. 2.5:

						0,
			f (t)
	Е						E
	Е						E


						t
						f (t) 1
							E
t1				t	t	t1
		1
		Рис. 2.5				0,

(t t1),

(t1 t),

t t1,

t1 t 0 ,

0 t t1, t t1.

В силу четности функции находим косинус-преобразование Фурье:

(t1 t)

2E sin 2

sin t

sin

tdt

(1 cos t )

Постройте график этой функции самостоятельно.

f (t)

Пример 2.5.

(t2 1)2

Поскольку функция является нечетной, то находим синус-

преобразование Фурье:

i t

S( ) V ( ) Im

2 (1 t

)

Так как f (t) 0

при t для вычисления интеграла можно

использовать теорему о вычетах:

f (t)e i tdt 2 i res f (tk )e i tk ,

Im tk

k 1

Таким образом, учитывая, что подынтегральная функция имеет полюс второго порядка в нижней полуплоскости, спектральная плотность запишется в следующем виде:

i t

(t i)

S( ) Im

2 i res

)

(t i)

(1 t

t i

i t

ti e

)(t i)

2(t i)e

Im i

(t i)

t i

(1 ti )(t i) 2t

i t

(1 )( 2i) 2i

Im i

Imi

(t i)

t i

2i 2 i 2i

Пример 2.6. Найти преобразование Фурье для функции Гаусса

f (t) e

(рис. 2.6).

f (t)

2> 1

0	t

Рис. 2.6

Для вычисления спектральной плотности

			t 2


	1			e i t dt
S( )	1	e
S( )		e
	2

покажем предварительно, что интеграл Пуассона


I	e t 2 dt 1.

Действительно, вычисляя квадрат интеграла в полярной системе координат, получаем


I 2	e x2 dx	e y2 dy	e (x2 y2 )dxdy

			29
2		2		1		2
2

d e			d 2		e			1.
d e			d 2	2	e			1.
				2
0	0						0
0	0						0

Далее сведем вычисление интеграла Фурье к интегралу Пуас-

сона:

								t		2	i t	2		2		2 2
								t			i t


			1									4				4
S ( )			1		e							4				4
S ( )		2			e
		2
						2 2					t	i 2


			1									2
			1		e		4		e					dt
					e		4		e					dt
		2

					2 2											2 2
	1			e 4											e 4
	1							e z2 dz
								e z2 dz					2
	2												2

Здесь при вычислении интеграла ввели переменную

zt i . График S( ) изображен на рис. 2.7.

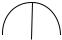
Рис. 2.7

Покажем, как по спектральной плотности восстановить функцию f (t) , то есть найти обратное преобразование Фурье.

Пример		2.7. По известной спектральной плотности
S( )	1	найти обратное преобразование Фурье.

	2 2 2

30
	1	e	i t
f (t) S( )ei t d	1	e		d .
f (t) S( )ei t d				d .
	2 2 2

Для вычисления интеграла используем теорему о вычетах, записанную через переменную с учетом того, что подынтегральная функция имеет простой полюс в верхней полуплоскости k i .

S( )ei t d 2 i

res(S( k )ei kt );

k 1

Im k 0;

S( )

при .

i t

i e

i t

e t .

f (t)

2 i res

2.3. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБР АЗОВАНИЙ ФУРЬЕ

Рассмотрим основные свойства преобразований Фурье.

1. Линейность

Пусть функции f (t) и g(t) имеют своим преобразованием

Фурье функции S f ( ) и Sg ( ) соответственно. Тогда для функции
f (t) (t)	преобразованием	Фурье	служит	функция

S f ( ) Sg ( ) : f (t) g(t) S f ( ) Sg ( ) .

Это свойство следует непосредственно из свойств определенного интеграла, которым и является преобразование Фурье.

2. Симметрия

Если S( ) − преобразование Фурье для функции f (t) , то f ( ) является преобразованием Фурье для функции S(t). Рассмотрим это на примерах.

Пример 2.8.

Преобразованием Фурье для функции f (t) exp( t ) является

функция S( )	1		1	. Легко проверить, что преобразованием
		1 2

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.09.20191.76 Mб2К р № 2 для ГФ.doc
#
10.05.2015540.67 Кб63к.р. №1.doc
#
09.11.2018317.44 Кб2К2.doc
#
09.11.2018288.77 Кб2К3.doc
#
25.11.2019538.62 Кб7кабели электро.doc
#
16.03.20162.06 Mб62Казунина Г. А..pdf
#
03.05.2019143.36 Кб9КВ-АП_Эксплуатационные_свойства.doc
#
10.05.2015288.35 Кб22КДиП.pdf
#
22.11.201947.34 Кб5кейс 1.doc
#
22.11.201951.76 Кб1кейс 2.docx
#
22.11.201947.68 Кб5кейс 4.docx