2012

Министерство транспорта российской федерации Федеральное агентство железнодорожного транспорта

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

А. В. Гущин

ТЕОРИЯ И АЛГОРИТМЫ:

нечеткие арифметика, кластеризация, синтез знаний и принятие решений в условиях лингвистической неопределенности

Допущено Учебно-методическим объединением вузов по университетскому политехническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки 230100 – «Информатика и вычислительная техника»

Самара

2012

2

УДК 681.3.068., 519.254. ББК 32.818

Г 98

Рецензенты:

доктор техн. наук, профессор кафедры «Информационно-измерительная техника»

Самарского государственного технического университета

П. К. Ланге;

доктор техн. наук, профессор, заведующий кафедрой «Системы связи» Поволжского государственного университета

телекоммуникаций и информатики

В. В. Васин

Гущин А. В.

Г 98 Теория и алгоритмы: нечеткие арифметика, кластеризация, синтез знаний и принятие решений в условиях лингвистической неопределенности : учеб. пособие для вузов / А.В. Гущин ; Самарский гос. ун-т путей сообщения. – Самара : СамГУПС, 2012. – 96 с.

ISBN 978-5-98941-176-4

Учебное пособие содержит теорию и практические сведения по базовым интеллектуальным технологиям для магистрантов специальности «САУ». Приведены примеры алгоритмического программирования основных методов и операций, которые обобщены в теории нечетких множеств. Задания практической части каждой главы ориентированы на аудиторное исполнение магистрантами в присутствии преподавателя. Актуальность тем, представленных в издании, обоснована современными направлениями развития методов идентификации, управления, обработки ассоциативных образов, знаковых изображений и накопления знаний. В этих случаях математические модели формально трудны к описанию, реализации, восприятию, и экспертное представление становится доминирующим фактором в обозначении входных и выходных данных решаемых задач на основе нечетких логических посылок. Данное учебное пособие может быть рекомендовано для магистрантов специальности «Системный анализ и управление».

Материалы пособия могут быть основой курсовых, выпускных квалификационных работ, темы которых связаны с использованием математического аппарата на основе нечеткой логики.

УДК 681.3.068., 519.254. ББК 32.818

СамГУПС, 2012Гущин А.В., 2012

ISBN 978-5-98941-176-4

3

3.2.Нечеткая импликация …………………………………………………….. 13

3.3.Композиция бинарных нечетких отношений ……….………………….. 16

4. НЕЧЕТКИЕ ОБОБЩЕНИЯ НА АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ ………… 21

4.1.Нечеткая арифметика произвольных чисел, представленных

5.1.Кластеризация с-средних ……………………………………………….. 31

5.2.Нормы кластерного анализа ………………………................................... 39

6.3.Синтез нечетких правил на основе нечеткой кластеризации …………. 59

7.ОСНОВЫ НЕЧЕТКОГО ВЫВОДА. КОМПОЗИЦИОННОЕ ПРАВИЛО НЕЧЕТКОГО ВЫВОДА Л.ЗАДЕ ……………………………………………...…. 63

8.АППРОКСИМАЦИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ

ПАРАМЕТРИЧЕСКИМИ ФУНКЦИЯМИ …………………………………….… 66

9.УПРАВЛЕНИЕ И ПРИНЯТИЕ РЕШЕНИЙ В РАЗВИТИИ ТЕХНИЧЕСКИХ СИСТЕМ НА ОСНОВЕ НЕЧЕТКИХ МНОЖЕСТВ ……………………………. 70

9.1.Оценка риска модернизации технических систем в задачах содействия

принятию решения ………………………………………………………… 70

9.2.Упрощенная оценка риска модернизации технических систем ……….. 89

4

ПРЕДИСЛОВИЕ

Вниманию обучающихся автор пособия предлагает результаты отлаженных базовых алгоритмов, решающих математические и прикладные задачи на основе интеллектуальных технологий. Практическая часть пособия рассчитана на проведение занятий при непосредственном участии преподавателя, несмотря на подробное изложение алгоритмов и основ теории в самом издании. Это связано с тем, что достижение целей аналитических расчетов с учетом нечетких обобщений на логические и арифметические операции не всегда понятны учащимся из-за отсутствия еще достаточного опыта в переложении нечеткой теории на фактические задачи. Методика анализа и понимания алгоритмов формировалась в результате проводимых автором курсов по интеллектуальным системам и технологиям с использованием в практике расчетов математического пакета Mathcad. Учащимся не следует полагаться на понятие материала по интеллектуальным технологиям лишь по факту прочтения популярных изданий на данную тему. Кажущаяся простота изложения в сравнении, например, с системным анализом и теорией функций, содержит массу нюансов и нетривиальных вопросов, возникающих при непосредственном переходе к практическому решению. Следует помнить, что интеллектуальные технологии не изобилуют теоретическим материалом, а лишь используют нечеткое обобщение математической логики, отображений и арифметических расчетов в своих действиях при достижении результата. Здесь переменные и системные конструкции организации нечеткого вывода являются формами представления и обработки знаний. Методологически правильно нужно понимать, что дисциплины, основанные на нечетких множествах, не способны к теоретическому развитию на принципах строгой математической дедукции. Попытки составлять теоремы, леммы на заданную тему являются методологической ошибкой − в нечеткой теории нет од- нозначности отображений, биекции и не определены никакие типы сходимо- сти. А значит, не доказуема традиционно однозначность решения. Цель развития и использования интеллектуальных технологий должна быть очень проста и понятна − она всегда практическая и принадлежит конкретной прикладной области, соответственно обладая узкой специализацией. Но у данных технологий, в сравнении с построенными на формализме, есть основное преимущество − они игнорируют массу неопределенностей, которые порой требуют сложнейших математических моделей. Здесь нужна специальная форма (формула) знаний для достижения решения. Причем знания формализует эксперт, по типу своей деятельности порой далеко отстоящий от приемов математического моделирования. Естественно, что в роли эксперта может выступать и математик,

5

например, специалист по вероятностным моделям. По этой причине часто возникают системные рассогласования в подходе к нечеткому моделированию. Экспертные знания математика в нечетких технологиях не имеют никаких преимуществ перед экспертными оценками экономиста, биолога, социолога и т.д. Вся ценность для приемов нечеткого моделирования заключается только в эмпирическом опыте конкретного специалиста-эксперта. Традиционной ошибкой, например экспертов по вероятностным моделям, является их интуитивное представление о том, что они обладают большим знанием о свойствах функций принадлежностей, чем экономист или биолог. Это будет являться типичным заблуждением. Нельзя формы представления знаний (типа функций принадлежностей) математически ассоциировать, например, с вероятностными законами и проводить какие-либо подобные аналогии! Функция принадлежности продукт эмпирический. Выражение конкретного знания в конкретной области. Закон распределения в свою очередь − продукт четкой биекции, результат существования измеримой случайной величины и ее вероятностной функции. В нечетких технологиях ничего похожего не определено, даже нет пространства для алгебраических полей и нет свойств непрерывности относительно линейных операций. Это потому, что нет подобного уровня абстрагирования в экспертном мышлении, знании и в их приложении к практической деятельности. Схема мыслительного хода решения не может быть формально математически строго описана и обосновывается на специфических экспертных представлениях в виде причинно-следственных суждений. Подобные логические схемы решений существуют уже в немалом количестве − нет смысла их перечислять и типизировать. Есть основной смысл понимать их на примерах данного издания, чтобы в дальнейшем сделать успешный переход к проектированию новых систем на основе нечеткой теории множеств и соответствующих алгоритмов.

Каждая глава пособия и ее подразделы представляют собой отдельные блоки теоретических и практических сведений по отдельной нечеткой технологии с заданием и контрольными вопросами. Выполнять задания желательно последовательно, т. к. текущее содержание задания может содержать ссылки на использование результатов предыдущих работ. Графические решения и примеры программных листингов приведены в нотации входного языка пакета Mathcad. Подразделы, содержащие примеры программ, выделены шрифтом с равной шириной символов, что соответствует стилю написания машинных текстов.

В начале курса обучения студенты должны владеть базовыми приемами программирования в среде Mathcad.

6

1. ОСНОВЫ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ

Теория. Н е ч е т к о е м н о ж е с т в о . Нечеткое множество (fuzzy set) представляет собой совокупность элементов произвольной природы, относительно которых нельзя с полной определенностью утверждать – принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет. Другими словами, нечеткое множество отличается от обычного множества тем, что для всех или части его элементов не существует однозначного ответа на вопрос: «Принадлежит или не принадлежит тот или иной элемент рассматриваемому нечеткому множеству?» Можно этот вопрос задать по другому: «Обладают или нет его элементы некоторым характеристическим свой- ством, которое может быть использовано для задания этого нечеткого множества?»

Для построения нечетких моделей систем само понятие нечеткого множества следует определить более строго, чтобы исключить неоднозначность толкования тех или иных его свойств. Оказалось, что существуют несколько вариантов формального определения нечеткого множества, которые, по сути, отличаются между собой способом задания характеристической функции данных множеств. Для нечетких множеств нечеткая функция принадлежности есть первый пример обобщения четкой принадлежности элемента множества на нечеткую принадлежность. Точнее замена четкой градации «Элемент принадлежит или не принадлежит множеству» на монотонный интервал действительных чисел – степеней принадлежности элемента множеству, заключенных между 0 (принадлежит) и 1 (не принадлежит), включая и сами эти значения.

М а т е м а т и ч е с к о е о п р е д е л е н и е н е ч е т к о г о м н о ж е с т в а . Формально нечеткое множество A определяется как множество упорядоченных пар или кортежей вида: <х,µA (x) >, где х является элементом некоторого универсального множества или универсума X, a µA(x) — функция принадлежно- сти, которая ставит в соответствие каждому из элементов х Х некоторое действительное число из интервала [0,1], т. е. данная функция определяется в фор-

При этом значение µA(x) = 1 для некоторого х Х означает, что элемент х определенно принадлежит нечеткому множеству Α, а значение µA(x)=0 означает, что элемент x определенно не принадлежит нечеткому множеству А.

Формально конечное нечеткое множество будем записывать в виде:

А ={<x1, µA (x1) >, <x2, µA (x2)>,…, <xn, µA (xn)>}, а в общем случае – в

виде:

7

А ={<x, µA (x) >}.

П у с т о е н е ч е т к о е м н о ж е с т в о . В теории нечетких множеств сохраняют свой смысл некоторые специальные классические множества. Так, например, пустое нечеткое множество или множество, которое не содержит ни одного элемента, по-прежнему обозначается через Ø и формально определяется как такое нечеткое множество, функция принадлежности которого тождественно равна нулю для всех без исключения элементов: µØ = 0. В этой связи уместно упомянуть о том, что характеристическая функция обычного пустого множества также тождественно равна нулю для каких бы то ни было элементов:

хØ = 0.

У н и в е р с у м . Что касается другого специального множества, то так называемый универсум, обозначаемый через X, уже был использован выше в качестве обычного множества, содержащего в рамках некоторого контекста все возможные элементы. Формально удобно считать, что функция принадлежности универсума как нечеткого множества тождественно равна единице для всех без исключения элементов: µx = 1.

Н о с и т е л ь н е ч е т к о г о м н о ж е с т в а . Носителем нечеткого множества А называется обычное множество AS , которое содержит те и только те элементы универсума, для которых значения функции принадлежности соответствующего нечеткого множества отличны от нуля. Математически носитель

Иногда носитель нечеткого множества обозначают через supp(A), где supp

— первые буквы английского слова support. В данном издании не будет использоваться это обозначение, поскольку оно может быть ошибочно ассоциировано с обозначением рассматриваемой ниже функции sup(x).

Н о р м а л ь н о е н е ч е т к о е м н о ж е с т в о . Нечеткое множество A называется нормальным, если максимальное значение его функции принадлежности равно 1. Формально это означает, что для нормального нечеткого множе-

если условие (1.3) не выполняется, то такое нечеткое множество называется

субнормальным.

Контрольные вопросы

1.Перечислите проблемы в вопросах моделирования, управления, которые приводят к необходимости использованию аппарата нечетких множеств.

2.Нечеткость и традиционная математика − основные концептуальные отличия в представлении характеристических принадлежностей.

3.Определение нечеткого множества, универсума.

8

2.ПРЕДСТАВЛЕНИЯ НЕЧЕТКИХ МНОЖЕСТВ КУСОЧНО-ЛИНЕЙНЫМИ ФУНКЦИЯМИ

Теория. Формальное определение нечеткого множества не накладывает никаких ограничений на выбор конкретной функции принадлежности (ФП) для его представления. Однако на практике удобно использовать те из них, которые допускают аналитическое представление в виде некоторой простой математической функции. Это упрощает не только соответствующие численные расчеты, но и сокращает вычислительные ресурсы, необходимые для хранения отдельных значений этих функций принадлежности. Необходимость типизации отдельных функций принадлежности также обусловлена наличием реализаций соответствующих функций в рассматриваемых далее инструментальных средствах.

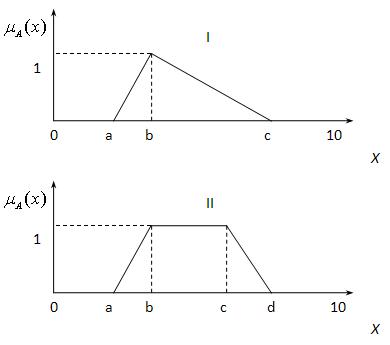
Рис. 1. Графики функций принадлежности:

I – треугольной формы, где a, c – пессимистическая оценка, b – оптимистическая;

II – трапециевидной формы, где a, d – пессимистическая оценка, а интервал [b,c] – оптимистическая

В качестве основного типа рассмотрим кусочно-линейные функции принадлежности, которые состоят из отрезков прямых линий, образуя непрерывную или кусочно-непрерывную функцию. Их еще можно называть экспертны- ми функциями по доступности и простоте понимания нечеткого представления ими принадлежностей экспертами различных прикладных областей. Наиболее

9

характерным примером таких функций являются «треугольная» (рис. 1, I) и «трапециевидная» (рис. 1, II) функции принадлежности. В нашем случае каждая из этих функций задана на универсуме Х = [0,10], в качестве которого выбран замкнутый интервал действительных чисел. В общем случае выбор универсума может быть произвольным и не ограниченным никакими правилами.

Нечеткое множество вполне определяется своей функцией принадлежности – это понятие используется как синоним нечеткого множества.

Пример описания. Первая из этих функций принадлежности (рис. 1, I) в общем случае может быть задана аналитически следующим выражением:

где a, b, c – некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: a< b<c.

Трапециевидная функция принадлежности (рис. 1, II) в общем случае может быть задана аналитически следующим выражением:

где а, b, с, d – некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: а< b< c< d.

Пример программы. Пусть trim и trap имена программных функций построения треугольника и трапеции соответственно. Обратите внима-

ние, как в примере задается положительный и отрицательный универ-

сум. Задание трапеции (2.2) и треугольника (2.1) на положительном универсуме:

Задание трапеции и треугольника на универсуме с отрицательными

значениями:

10