Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2012

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

1.79 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

4. НЕЧЕТКИЕ ОБОБЩЕНИЯ НА АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ

Принцип обобщения утверждает1, что отображение f и совокупность не-

четких множеств A1	, A2 ,..., Ak	однозначным образом порождают нечеткое ото-
бражение F : X 1 × X 2	× ... × X k	→ X , функция принадлежности которого опреде-
ляется по следующей формуле:
µF (< x1	, x2 ,..., xk , x >) = min{µ A1 (x1 ),µ A 2 (x2 ),...,µ Ak (xk )}		(4.1)
для всех кортежей < x1 , x2 ,..., xk , x > X 1 × X 2 × ... × X k × X ,			таких что
x = f (< x1 , x2 ,..., xk >) .

4.1.Нечеткая арифметика произвольных чисел, представленных кусочно-линейными функциями

Теория. Для нечетких чисел и интервалов в общем случае с использованием принципа обобщения (4.1) могут быть определены аналоги обычных арифметических операций. В этом случае расширенные бинарные арифметические операции (сложение, вычитание, умножение и деление) для нечетких чисел и интервалов определяются через соответствующие операции для обычных действительных чисел.

ПустьΑ иΒ — произвольные нечеткие числа (нечеткие интервалы: треугольники и трапеции) с функциями принадлежности µΑ (x)иµΒ (y)соответственно.

С л о ж е н и е . Операция сложения нечетких чисел (интервалов) обозначается через Α + Β = C = {z,µc (z)}, где функция принадлежности результата µc (z )определяется по формуле:

µ c ( z ) = sup {min {µ Α (x ),µ Β (y )}}.	(4.2)
z = x + y

В ы ч и т а н и е . Операция вычитания нечетких чисел (интервалов) обозначается через Α − Β = C = {z,µc (z)}, где функция принадлежности результата µc (z ) определяется по формуле:

µ c ( z ) = sup {min {µ Α (x ),µ Β (y )}}.	(4.3)
z = x − y

У м н о ж е н и е . Операция умножения нечетких чисел (интервалов) обозначается через Α Β = C = {z,µc (z )}, где функция принадлежности результата µc (z ) определяется по формуле:

1 Принцип обоснован классиком теории нечетких множеств Л. Заде.

µ c ( z ) = sup {min {µ Α (x ),µ Β (y )}}.	(4.4)
z = x y

Д е л е н и е . Операция деления нечетких чисел (интервалов) обозначается через Α ÷ Β = C = {z,µc (z )}, где функция принадлежности результата µc (z )определяется по формуле:

µ c ( z ) = sup {min {µ Α (x ),µ Β (y )}}.	(4.5)
z = x ÷ y

В выражениях (4.2)–(4.5) справа от знака равенства супремум берется по каждому из совокупности значений элементов универсума, которые в свою очередь являются результатом соответствующей обычной арифметической операции над численными значениями элементов универсума исходных нечетких чисел (интервалов). Другими словами исходное множество для sup формируется на основании принципа (4.1).

Пример описания. Подготовка парных векторов, представляющие функции принадлежности двух слагаемых:

i := 0.. 3		j := 0.. 4				4	0.5
	2		0.4			5		0.6
						5		0.6
x1:=	3	y1 :=	0.7	x2	:=	6	y2 := 0.85 .
x1:=	4	y1 :=	0.95	x2	:=	6	y2 := 0.85 .
	4		0.95					0.55
						7		0.55
	5		0.65
						8		0.4

Рассчитываем всевозможные пары четкого результата операции для формирования числовой четкой структуры − матрицы М, которая будет являться элементом x нечеткого отношения (4.1) при формировании результата обобщенной операции:

					6	7	8	9	10

M		:= x1 + x2		M =	7	8	9	10	11	.
M	i, j	:= x1 + x2		M =	8 9				12	.
	i, j	i	j		8 9		10	11	12

					9	10	11	12	13

Теперь имеем все элементы нечеткого отношения, по которому результат операции сложения формируется следующим образом.

•Выбираются из матрицы М одинаковые значения универсума − последовательное расположение в порядке возрастания данных значений будет формировать новый универсум результата.

•Для выбранных значений определяются координаты − порядковый индекс строки и столбца матрицы М. Например, для числа универсума 7 выбира-

ем две пары (1,0) и (0,1).

Пример программы.

• Отрабатываем оператор min (часть формулы (4.2)): по каждой паре координат цифры 7 находим принадлежности векторов, соответственно 1-я координата это индекс вектора y1 и 2-я координата − индекс вектора y2. Получаем результат из двух нечетких принадлежностей для универсума 7: min(0.7,0.5) и min(0.4,0.6).

• Завершаем вычисления результата для универсума 7, выбирая макси-

мальное значение принадлежности: max(min(0.7,0.5), min(0.4,0.6)) = 0.5.

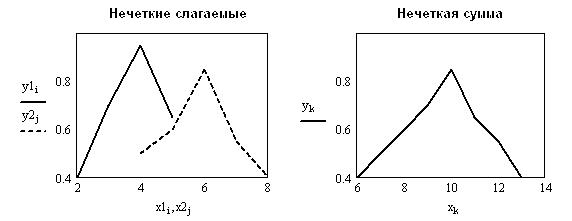
Для практического закрепления навыков сделайте расчет еще для нескольких значений универсума и сравните с тестовым результатом (рис. 4).

Рис. 4. Тестовый результат нечеткой суммы

Результат рассмотренной операции можно привести как элемент нечеткого множества, составленный из пар универсума xT = (6 7 8 9 10 11 12 13) и при-

надлежностей нечеткой суммы: yT = (0.4 0.5 0.6 0.7 0.85 0.65 0.55 0.4) .

Приводятся фрагменты кода, полностью автома-

тизирующие алгоритмы нечетких арифметических операций. Фрагменты показаны частями, демонстрируя ход расчетов. Назначение примера − способствовать читателю в создании единой универсальной процедуры выполнения нечетких арифметических действий с числами, представ-

ленными кусочно-линейными функциями.

Исходные данные и тип операции (нечеткая сумма) те же, что и в примере описания. Далее следующий порядок действий.

• Составляем матрицу значений универсума по результату четкой операции. Для операций, отличных от сложения, сделайте замену зна-

ка «+» на соответствующую операцию.

V :=	k ← 0
	for i 0.. 3
	for		j 0.. 4
					x1 + x2
					x1 + x2
						i	j
		v	k	←			i
			k				i

							j
		k ← k + 1
	return		v

Обратите внимание, что возвращаемый результат содержит вектор всех значений универсума и индексы, указывающие позиции операндов сло-

жения в первом и втором векторе принадлежностей у1 и у2.

• Формируем функцию f для заполнения матричной формы M.

f(i, j) := return (V )	M := matrix(length (V) , 3, f)
i	j

• Сортируем матрицу М по возрастанию универсума:

M:=csort(M,0),

где M<0> - значения универсума; M<1> - принадлежности 1-го вектора данных; M<2> - принадлежности 2-го вектора данных.

• Отлаживаем процедуру выполнения max-min композиции для дубли-

рованных значений универсума с формированием шкалы универсума и с вычислением нечетких принадлежностей по ней, используя формулу

(3.1):

Vfc := argx0 ← MS0 , 0

r0 ← min y1(MS0 , 1) , y2(MS0 , 2)

k ← 0

stop ← last(MS 0 )

for i 1.. stop if stop ≥ 1


r	← max r		, min y1	(MSi , 1)	, y2	(MSi , 2)	if MS		argx
k		k		(MSi , 1)		(MSi , 2)		i, 0	k

otherwise

k ← k + 1

rk ← min y1(MSi , 1) , y2(MSi , 2)

argxk ← MSi, 0

argx return

• Вызываем процедуру и делаем отдельные присвоения: для x воз-

вращаем шкалу универсума, а для y – нечеткие принадлежности.

x := Vfc0

y := Vfc1

Результат аналогичен примеру описания.

xT = ( 6 7 8 9 10 11 12 13)

yT = ( 0.4 0.5 0.6 0.7 0.85 0.65 0.55 0.4)

Практическое задание: пошаговое и автоматизированное выполнение нечетких арифметических операций.

Содержание задания:

•Получить значения исходных нечетких чисел, как индивидуальное задание от преподавателя.

•Ознакомиться с теорией арифметических операций нечетких чисел, представленных кусочно-линейными функциями по данным раздела «Пример описания».

•Открыть новый файл Mathcad. Выполнить заданные нечеткие арифметические операции над полученными числами по выражениям (4.2)–(4.5). В пошаговом выполнении задания руководствоваться разделом «Пример описания».

Результат практики: продемонстрировать результат нечетких арифметических операций графически.

Дополнительно: предложить собственную схему алгоритма автоматизации операций нечеткой арифметики над нечеткими числами в кусочно-линейном представлении. Сделайте попытку реализации и отладки алгоритма. Можно это задание выполнить вне аудитории в качестве самостоятельной работы.

Контрольные вопросы

1.Чем в первую очередь вызвана сложность и громоздкость алгоритмов нечеткой арифметики для кусочно-линейных функций?

2.Есть ли систематизирующая особенность в формировании матрицы M элементов универсума в приводимых примерах и как можно изменить алгоритм

сучетом этой особенности?

3.Будет ли обеспечена мономодальность результата при нечетком делении чисел, представленных кусочно-линейными функциями?

4.2. L-R числа, интервалы и арифметические действия с ними

Нечеткие числа и интервалы в форме (L-R) функций − это непрерывные функции, асимптотически стремящиеся к нулю слева и справа от моды. Они представляют ассиметричную композицию левой L и правой функции R с отдельными параметрами крутизны, что позволяет воссоздать фактически любую

мономодальную форму нечеткого числа. Эти функции абсолютно непрерывны и обладают способностью дифференцироваться бесконечное число раз. Это, кроме числовых представлений, позволяет использовать их в качестве конкретных весовых распределений, параметры которых обладают свойством адаптации, например в нейрологических комбинаторных схемах. В данном разделе эти функции будут использоваться как операнды нечетких арифметических операций. Алгоритмическое представление этих операций будет представлено здесь гораздо проще, чем в разделе нечеткой арифметики кусочно-линейных функций.

Параметризация L-R функций, возможно, затрудняет их непосредственное задание экспертом, но те же параметры делают их идеальным средством в синтезе знаний, в аппроксимации полученных нечетких результатов и т.п. Эти вопросы будут рассмотрены в следующих разделах.

Теория. Нечеткие числа и интервалы, которые наиболее часто используются для представления нечетких множеств в нечетком моделировании, являются нормальными. Однако данные выше определения нечеткого числа и нечеткого интервала слишком общие, что затрудняет их практическое использование. С вычислительной точки зрения удобно использовать более конкретные определения нечетких чисел и интервалов в форме аналитической аппроксимации с помощью так называемых (L-R) функций. Получаемые в результате нечеткие

числа и интервалы в форме (L-R)	функций позволяют охватить достаточно ши-
рокий класс конкретных функций принадлежностей.
Функции L – типа и	R – т и п а. Функция L – типа (а также и R –

типа), в общем случае определяется как произвольная функцииL : R → [0,1]и R : R → [0,1] , заданная на множестве действительных чисел, невозрастающая на подмножестве неотрицательных чисел R+ и удовлетворяющая следующим дополнительным условиям:

L(−х) = L(х) , R(−x) = R(x) − условие четности;	(4.6)
L(0) = R(0) = 1 − условие нормирования.	(4.7)

Примерами L функций и, соответственно, R функций являются следующие функции, которые в общем случае могут быть заданы аналитически в виде:

f (x) = e−

;

(4.8)

f (x) =

;

(4.9)

1 +

где p – некоторый параметр, который удовлетворяет условию: p ≥ 0.

Н е ч е т к о е ч и с л о (L − R) − т и п а. Нечетким числом (L − R) − типа

будем называть нечеткую величину			B = {x,µ B (x)}, функция принадлежности
которой может быть представлена в форме композиции некоторой L –функции
и некоторой R – функции в следующем виде:
	a − x				если x ≤ a
L				,

	α					(4.10)
µ B (x) =		x − a

	R				,	иначе

			β

где α > 0 и β > 0 . При этом параметр α является модой или модальным значением нечеткого числа, а параметры α и β являются левым и правым коэффи- циентами нечеткости соответственно. Как видно из этого определения, при задании нечетких чисел (L − R) − типа могут использоваться, вообще говоря, две различные функции указанного вида, что существенно расширяет диапазон их возможных представлений.

Из данного определения следует, что нечеткое число (L − R) − типа с функцией принадлежности µB (x) при фиксированных L и R функциях вполне определяется тройкой своих параметров < a, α,β >, что оказывается весьма удоб-

ным для выполнения операций с подобными числами.
Н е ч е т к и й и н т е р в а л (L − R) − т и п а . Нечетким	интервалом
(L − R) − типа будем называть нечеткую величину B = {x, µ B (x)},	функция при-

надлежности которой может быть представлена в форме композиции некоторой L функции и некоторой R функции в следующем виде:

		a − x
	L			,
	L			,
			α
µ B	(x) =		1,
		x − b
	R			,
	R		β	,
			β

где α > 0 иβ > 0 . При этом параметры a

если	x ≤ a
если	a < x < b	(4.11)
иначе

и b определяют ядро нечеткого интер-

вала (a < b) и называются соответственно нижним и верхним модальными зна- чениями нечеткого интервала. Параметры α и β по-прежнему называются ле-

вым и правым коэффициентами нечеткости соответственно. Следует отме-

тить, что нечеткий интервал (L − R) − типа часто называют толерантным нечетким числом (L − R) − типа.

Функция принадлежности µ B (x) нечеткого интервала (L − R) − типа при фиксированных L и R функциях вполне определяется четверкой своих пара-

метров < a,b, α,β >, что оказывается весьма удобным для выполнения операций с подобными интервалами. Чтобы отметить тот факт, что нечеткий интервал является (L − R) − типа, будем его обозначать специальным образом:

BLR =< a,b,α,β >LR .

Пример описания операций над нечеткими числами и интервалами (L − R) − типа. При определении операций над нечеткими числами и интервалами(L − R) − типа следует исходить из следующих соображений. Результат арифметических операций сложения, вычитания, деления и умножения должен быть точно или приблизительно равен некоторому нечеткому числу или интервалу с теми же функциями L – типа и R – типа, а параметры α и β результата должны некоторым однозначным образом зависеть от аналогичных параметров исходных нечетких чисел и интервалов (L − R) − типа.

С этой целью для определения аналогов обычных арифметических операций над нечеткими числами и нечеткими интервалами (L − R) − типа целесообразно использовать принцип обобщения (4.23). Замечательным свойством определенных таким способом арифметических операций (сложение, вычитание, умножение и деление) является то, что они определяются на основе значений


соответствующих параметров их (L − R) − представлений.
Пусть ALR и BLR –		произвольные нечеткие числа (L − R) − типа, заданные
параметрически в виде:		ALR =< a1 , α1 , β1 >LR и BLR =< a2 ,α2 ,β2		>LR .
С л о ж е н и е .	Операция сложения нечетких чисел (L − R) − типа обознача-
ется через ALR + BLR	= CLR =< a,α , β > LR ,		где параметры a, α и β	результата опре-
деляются следующим образом:
	a = a1 + a2 , α = α1		+ α2 , β = β1 + β2 .	(4.12)
В ы ч и т а н и е . Операция вычитание нечетких чисел (L − R) − типа обо-

значается через ALR − BLR = CLR =< a,α , β > LR , где параметры a, α и β результата определяются следующим образом:

a = a1 − a2 , α = α1 + β2 , β = β1 + α 2 .	(4.13)
Операции умножения и деления нечетких чисел ( L − R ) − типа могут быть оп-
ределены при выполнении некоторых дополнительных условий.
У м н о ж е н и е положительных нечетких чисел (L − R) − типа ALR	и BLR , т.
е. носители которых являются подмножествами R+, а модальные	значения

a1 > 0 и a2 > 0 . Операция умножения таких нечетких чисел (L − R) − типа обозначается через ALR • BLR = CLR =< a,α,β >LR , где параметры a, α и β результата определяются следующим образом:

	a = a1a2 , α = a1α2 + a2 α1 , β = a1β2 + a2β1 .				(4.14)
У м н о ж е н и е		нечетких чисел (L − R) − типа		ALR и BLR , для которых мо-
дальные значения разных знаков: a1 < 0 и			a2 > 0 .	Операция умножения таких
нечетких	чисел	(L − R) − типа	также	обозначается	через
ALR • BLR = CLR	=< a, α,β >LR , где параметры		a, α и β результата определяются
следующим образом:
	a = a1a2 , α = a2 α1 − a1β2 ,		β = a2β1 − a1α2 .		(4.15)
У м н о ж е н и е нечетких чисел (L − R) − типа ALR и BLR , для которых мо-

дальные значения отрицательные: a1 < 0 и a2 < 0 . Операция умножения таких

нечетких	чисел	(L − R) − типа	также	обозначается	через
ALR • BLR = CLR	=< a, α,β >LR , где параметры		a, α и β	результата определяются
следующим образом:
	a = a1a2 ,	α = −a2β1 − a1β2 ,	β = −a2 α1	− a1α2 .	(4.16)

Д е л е н и е положительных нечетких чисел (L − R) − типа ALR и BLR , т. е. носители которых являются подмножествами R+, а модальные значения a1 > 0 и a2 > 0 . Операция деления таких нечетких чисел (L − R) − типа обозначается че-

рез ALR	÷ BLR = CLR	=< a,α,β >LR ,						где параметры a, α и β результата определя-
ются следующим образом:
	a = a / a				2	, α = (a β			2	+ a		α		) / a 2 ,	β = (a α		2	+ a	β	) / a 2	(4.17)
		1			2		1		2	2			1	2		1	2	2	1	2
О б р а т н о е		н е ч е т к о е							ч и с л о для положительного нечеткого числа
(L − R) − типа ALR , т. е. носитель которого является подмножеством R+, а мо-
дальное значение a1			> 0 . В этом случае обратное нечеткое число обозначается
через C	−1 =< a,α,β >			LR			, параметры которого a, α									и β		определяются следую-
	LR			LR
щим образом:
						a = 1/ a ,		α = β			1		/ a 2 , β = a / a 2 .								(4.18)
							1				1			1	1	1

Пример программы. Ознакомьтесь с примером организации вещест-

венной шкалы универсума. Обратите внимание, как можно задавать шаг дискретизации между целыми значениями шкалы. В данном случае шкала ограничена 0..N-1, дискретизация единичного интервала 10.

		i
N := 20 stop := N 10	i := 0.. (stop ) − 1 xi :=		N

		stop − 1

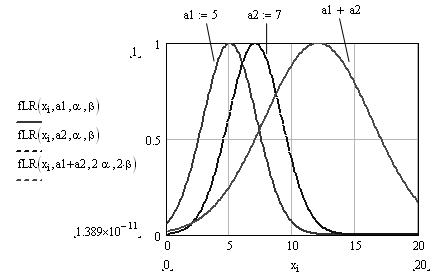
Задаем операнды (моды чисел (L − R) − типа) и определяем нечеткую

сумму (рис. 5).

Практическое задание: получить навыки процедурного программирования с использованием логических конструкций, организованных для вариант-

ного выбора. Запрограммировать и тестировать формулу отображения чисел (L − R) − типа. Произвести тест основных нечетких арифметических операций.

Содержание задания:

• Получить от преподавателя персональный вариант значений (по модам) для пары чисел (L-R) − типа.

Рис. 5. Исходные данные и результат суммы чисел (L–R) − типа

•Открыть новый файл Mathcad. Составить два варианта формулы для функции с именем LR по выражениям (4.8), (4.9). Задайте шкалу с дискретным шагом меньше единицы, используя раздел «Пример программы». Задав значение p:=2, протестируйте полученные формулы.

•Запрограммировать формулу числа (L-R) − типа по выражению (4.10), рекомендуемое в программе имя функции fLR(x).

•Отобразите полученные варианты исходных чисел графически, подобрав по своему усмотрению параметры α, β.

•Выполнить арифметические операции над числами, используя формулы

(4.12), (4.13) и (4.14).

Результат практики: продемонстрировать графически результат всех построений чисел (L-R) − типа и действий с ними.

Контрольные вопросы

1.Какие функции и почему получили большее распространение у экспертов для лингвистического представления знаний: кусочно-линейные или непрерывные (настраиваемые параметрами)?

2.Попробуйте обосновать связь или ее отсутствие между (L–R) функциями

ифункцией плотности распределения случайной величины.

3.С каким классом функций (L–R) функции структурно эквивалентны (изоморфны) по аналитическим свойствам.

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.20152.69 Mб1172. Технология возведения земляного полотна.doc
#
09.04.201599.02 Кб18200 иностранных слов.docx
#
15.11.2019377.34 Кб82002 Рабочая.doc
#
09.04.2015327.68 Кб702002.doc
#
09.04.201572.71 Кб462002.docx
#
15.03.20161.79 Mб442012.pdf
#
09.04.2015875.52 Кб272015.doc
#
09.04.20153.33 Mб2792034.doc
#
09.04.20151.04 Mб122045.doc
#
08.11.2019244.74 Кб1020591.doc
#
15.03.20161.63 Mб1502066.doc