2012

характеристик риска и важности для k-го фактора, k = 1, N , N – число факторов риска.

Веса факторов x1..xN в проекте модернизации обозначим вещественными функциями W 2(x1 ) ..W 2(xN ) . При этом выполняются условия нормировки

N

∑W 2(xk ) = 1, 0 ≤ W 2(xk ) ≤ 1, k = 1, N .

k=1

Всвою очередь функции веса jk -й характеристики риска k-го фактора xk

ключается в расчете нечетких матриц M k для каждого k-го фактора с формированием отношения общих степеней риска с учетом их весовых характеристик и с отображением данного отношения G :W 2 × (W1k × M k ) → R центроидным ме-

k =1,N

тодом G, где R – выход модели оценки риска по всей совокупности факторов.

Алгоритм 9.1

Шаг 1. Формирование N факторов риска модернизации ТС и совокупности их характеристик с последующим построением иерархической модели риска модернизации.

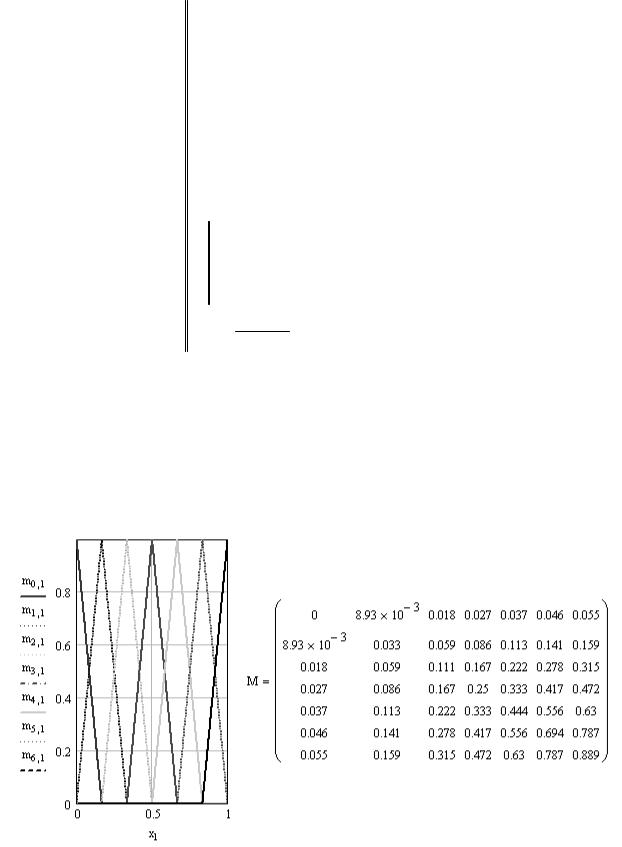
Шаг 2. Определение необходимого количества лингвистических переменных m (в табл. 7 их определено m = 11) для оценки степени истинности факторов риска (выход нечеткой модели риска) и их характеристик (вход нечеткой модели риска). Построение для sk ,• треугольных

функций принадлежности (2.1) в количестве nk m для каждого k-го

jk -й характеристики k-го фактора, значения элементов пар выбираются из диапазона m.

Шаг 3. Расчет матрицы Μ размерностью m × m производится путем приведения к четкости выражением (9.2) произведения нечетких чисел

деляется четкое значение лингвистической оценки риска. Это значе-

81

ние фиксируется по шкале универсума «степень риска» и определяется его пересечение с каждым t-м нечетким числом. Учитывая, что количество чисел m и что по числу характеристик фактора формируется nk строк из данных чисел, то нечеткая матрица M k k-го фактора будет иметь размерность nk × m (выход этапа I, рис. 22). В нормальную

Итак, Шаг 1 – Шаг 3 – это этап I, а Шаг 4 – Шаг 5 – этап II (рис. 22). Результат вычисления по модели оценки риска Шаг 1 – Шаг 5 далее передается в систему принятия решения модернизации ТС.

Пример программы по Алгоритму 9.1

Шаг 1. В примере используется массив m из семи функций принад-

лежности степеней риска и значимости 2-х факторов. Поэтому степени риска и значимости будут указываться i-м индексом к одной из ФП массива m. Объявляем эти функции по типу тре-

угольных с использованием конструкции trim():

82

где xl – это множество универсума отрезка [0,1] с малым ша-

гом; α и β – соответственно левая и правая характеристика нечеткости треугольных чисел, представленных i-й функцией принадлежности m.

Шаг 2. Для демонстрации конкретного решения выбираем два фак-

тора по индексу k. Описание характеристик факторов строим как числовые матрицы, где число столбцов соответствует ко-

личеству назначенных характеристик. Первый элемент столбца

– это индекс ФП из m для степени риска, второй индекс соот-

ветственно указывает на ФП степени значимости фактора:

Шаг 3. Расчет четкой матрицы M размерностью (N+1)×(N+1), содер-

жащей результат нечеткой корреляции ФП степеней риска и

значимости:

83

DCentr(r, i) := nr ← Nrr

ni ← Nri risk ← 0

cen_sum ← 0

left ← (nr αi) + (ni αr) right ← (nr βi) + (ni βr) modul ← nr ni

for k 0.. R

cen_step ← µtrim(xk, modul − left, modul, modul + right)

cen_sum ← cen_sum + cen_step risk ← risk + (xk cen_step )

risk

return

cen_sum

Mr, i := DCentr(r, i)

Это формула приведения к четкости центроидным методом (9.2)

результата нечеткой корреляции ФП (рис. 23), полученной на основании произведения треугольных ФП как чисел (L-R) – ти-

па (п. 4.2).

Рис. 23. Треугольные ФП степеней риска и значимости факторов с четкой матрицей M корреляции данных степеней

Строим функцию, которая выдаст ответ в виде нечеткого век-

тора из N+1 значений для любого элемента их М. Геометриче-

ски это значит, что ищется нечеткий уровень пересечения ка-

84

ждого элемента из M с каждой из N+1 ФП логической оценки степени риска и значимости:

Теперь можно перейти к расчету нечеткой матрицы риска mxk

размерностью nk × N + 1 для каждого k-го фактора:

Результат расчета нечетких матриц для первого и второго факторов:

Mrxk := submatrix(W1 , k, k, 0, cols(RIk) − 1) mxk

85

Mcols (Rc) := n ← rows(Rc) − 1 mxT ← 0

for r 0.. n mx ← Rcr

mxT ← stack (mxT, mx) if r > 0 mxT ← mx otherwise

return mxT

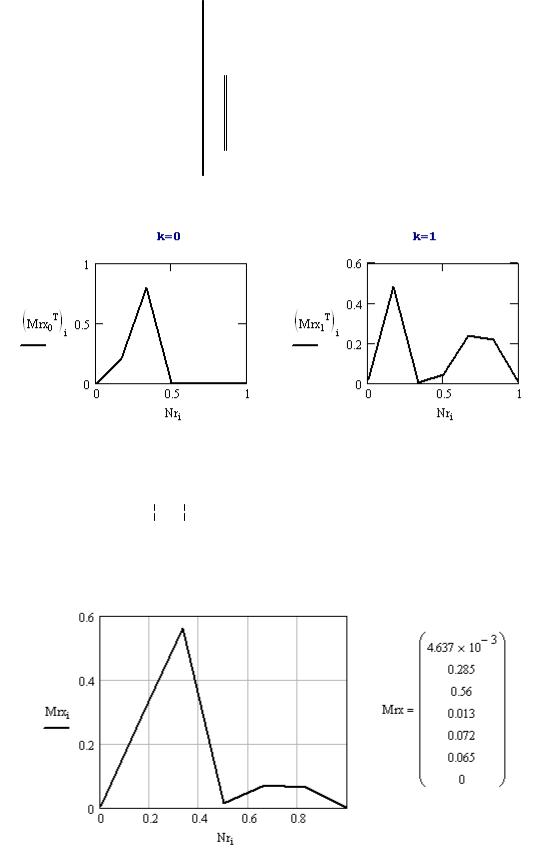
Результат нормализации на рис 24.

Mrx := ((W2)T Mcols (Mrx))T

Рис. 25. Синтез ФП риска модернизации всей системы

Шаг 5. Получение оценки общего риска устранением нечеткости Mrx

центроидным методом (9.2):

86

Centroid(µ , λ) := R ← length (µ) − 1 sumµx ← 0

sumµ ← 0 for k 0.. R

act_step ← µk

sumµ ← sumµ + act_step

sumµx ← sumµx + (λk act_step )

return sumµx sumµ

Ответ в форме четкого коэффициента риска модернизации всей

технической системы:

Centroid(Mrx, Nr) = 0.343

Практическое задание: оценка риска модернизации технической системы, где процесс модернизации представляется структурной иерархической моделью факторов модернизации с характеристиками их риска и значимости.

Содержание задания: исходные данные 4-х вариантов системы отображены в табл. 8 – 11. Предполагается использование индексов степеней риска и значимости от 0 до 7, хотя число степеней может быть изменено преподавателем.

Исходные данные по оценке факторов риска

Таблица 8

87

Таблица 10

Факторы xk , k = 1,4

С учетом большого объема программных построений алгоритма можно ограничиться Шагом 1 примера Алгоритма 9.1 и расчетом четкой матрицы нечетких корреляций степеней риска и значимости.

Результат практики: числовые модели выбранного варианта факторов и их весовые оценки в виде матриц (можно предложить собственный вариант, отличный от примера); графики ФП степеней риска и значимости факторов; матрица корреляций М.

Контрольные вопросы

1.Пояснить понятие сложной системы.

2.Дать определение структуры и подсистемы ТС.

88

3. Какая основная причина перехода от аналитических оценок к лингвистическим в моделях управления и идентификации?

9.2. Упрощенная оценка риска модернизации технических систем

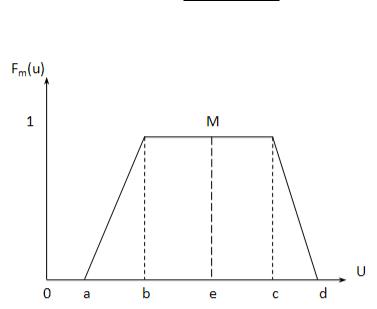
Теория. Для практических целей Алгоритм 9.1 существенно упрощается, если ввести операцию по снятию нечеткости трапецеидального нечеткого числа

М (рис. 26)

D(M ) = e = a + b + c + d . 4

Рис. 26. Снятие нечеткости трапецеидального нечеткого числа

Треугольное нечеткое число А, параметризованное тройкой (a, b, c), является частным случаем трапецеидального нечеткого числа М. В этом случае треугольное нечеткое число А может также быть представлено четверкой (a, b, b, c). Тогда снятие нечеткости значения D(A) треугольного нечеткого числа будет определяться с помощью зависимости

Базируясь на выражении (9.4), содержание иерархической структурной модели, показанной на рис. 21, может быть представлено в виде данных табл. 12. Здесь оценка риска Μ = D(r) × D(i) , где D(r) и D(i) – значения треугольных нечетких чисел со снятой нечеткостью, описанных соответственно степенью риска (r) и значимости (i). Отсюда упрощенный алгоритм оценки риска.

Алгоритм 9.2

Шаг 1. Совпадает с действиями Алгоритма 9.1 – Шаг 1 – Шаг 2.

89

Шаг 2. Расчет четкой матрицы Μ совокупности оценок риска, используя снятие нечеткости с термов способом трапеции.

Шаг 3. Оценка рисков отдельных факторов с использованием весовых коэффициентов характеристик риска и значения из Μ по индексам пары

Основным достоинством подхода во втором случае, не взирая на некоторую округленность результата, является то, что не требуется формировать нечеткие матрицы и оценки риска факторов для получения первостепенных составных векторов оценок риска. Кроме того, нет надобности выполнять сложные операции по снятию нечеткости в расчетах, использующих центроидный метод.

90