2012

6.СИНТЕЗ ЗНАНИЙ ТИПА ЛИНГВИСТИЧЕСКИХ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ И НЕЧЕТКИХ ПРАВИЛ

Конкретные числовые ФП являются отображением нечетких экспертных представлений, основанных на знании и эмпирическом опыте. В системе нечеткого моделирования и организации нечеткого вывода эксперт объявляет физическую величину как терм – существительное, под которое группируется совокупность терм-элементов, характеризующая изменения данной величины. Формальные детали такого подхода подробно описаны в [3], [5]. Коротко коснемся сути дела в вопросах формализма представления знаний в нечетких технологиях. Например, моделируется входная переменная технологического процесса, обозначается термом «Вода». Совокупность нечеткой оценки ее мгновенных температурных режимов выражается терм-элементами: «Холодная», «Теплая», «Горячая» и т. д., где каждый элемент – отдельная функция принадлежности. Элементы объединяет терм «Вода» по универсуму (измерению) температура. Ясно, что терм-элементы – конкретные одномодальные1 числовые функции. Их наличие и есть форма представления знаний эксперта о процессе изменения состояния входного вещества. Таким образом, процесс смыслового овеществления знаний в виде функций, или получение этих функций по результатам работы некоторого алгоритма, есть синтез знаний. Синтез нечетких принадлежностей – это центральная тема интеллектуальных технологий на основе теории нечетких множеств. Терм-элементы, воплощенные в числовые функции, являются подусловиями и подзаключениями элементарных импликативных конструкций – правил, системы которых композиционно агрегируют формулу нечеткого вывода (новое знание), приведение которой к четкости (дефаззификация) находит ответ (реакцию) модели на заданные воздействия.

Часто делаются попытки установить эквивалентность в определении моды терм-элемента экспертом и оценкой среднего по вероятности ожидания значения некоторой случайной величины. Автор издания сторонник теории, что никакой аналитической связи, эквивалентности случайного распределения и ФП не существует. Вероятность конкретной величины описана законом распределения лишь внешне похожим на одномодальные ФП. Вероятность и логическая истинность являются верхними границами (единицами) совершенно различных множественных абстрактных моделей, в данном случае вероятностного пространства и шкалы принадлежностей2. Закон распределения случайной величи-

1 Одномодальность терм-элемента есть адекватность суждений эксперта о единственном нечетком истинном значении параметра в окрестности моды.

2 Точнее для вероятности «Единица» – это верхняя граница измерения элементарных исходов; для четкой логики «Единица» – единственный не пустой элемент вырожденного множе-

51

ны и экспертное нечеткое представление − совершенно разные явления! Они не связанны изоморфно, тем более что изоморфизма нет в теории нечетких множеств, так как нет отображений со свойствами биекции, а если говорить об отношении ФП к вероятностям, то естественно отсутствует измеримая функция, а значит, и всякая связь со случайными явлениями! Мыслите системно и не допускайте подобных ошибок. В связи с этим в издании приведены примеры синтеза не затрагивающие спорные вопросы подобной связи. Конечно, не нужно утверждать, что нет причинно-следственной связи ФП и распределений случайных величин – она существует и является предельно сложной с точки зрения математической формализации. Нельзя ее устанавливать по свойствам эквивалентности и изоморфизма, проводить дедуктивную цепь доказательств. В издании есть пример оценки среднего времени разгона автомобиля по данным нечеткой кластеризации. Алгоритм примера только эмулирует поведение случайной величины – время разгона автомобиля. Установлена их смысловая связь через термы и обозначения. Но нет смысла устанавливать аналитическую связь случайности и экспертного смысла, т. к. кластеризация не предполагает использование априорной информации о распределении координат-признаков, без чего арифметическая оценка среднего по вероятности состояться не сможет!

Итак, ФП – конкретная числовая реализация знаний нечеткого представления о значении1. Фактически любое явление, которое измеряется вещественной шкалой, без особых затруднений может быть воспроизведено экспертом любой прикладной области в форме кусочно-линейной функции. Но в интеллектуальных технологиях значительный интерес представляют функции, которые синтезируются автоматически по результатам обработки измерений, или экспертных мнений. А если они еще и непрерывны и управляются параметрами

– то это класс важнейших функций, которые можно, например, использовать с градиентными методами в адаптивной настройке систем на нейрологическом базисе.

Рассмотрим кратко теорию и решение основных методов синтеза знаний. Первый метод − составление экспертных таблиц, он громоздок и прост. Читатель без труда освоит этот метод самостоятельно [7]. Поэтому сразу перейдем к методу парных сравнений.

6.1. Парные сравнения

Теория. При построении функций принадлежности по данному методу для каждой пары элементов универсального множества эксперт оценивает преиму-

ства – дистрибутивной ограниченной решетки; для нечеткой логики «Единица» – замыкание открытого множества вещественных принадлежностей к истинности.

1 А распределения вероятностей − конкретное вероятностное знаний о конкретном значении.

52

щество одного элемента над другим по отношению к свойству нечеткого множества. Такие парные сравнения удобно представлять следующей матрицей:

•1 – если преимущество элемента ui над элементом uj отсутствует;

•3 – если преимущество ui над uj слабое;

•5 – если преимущество ui над uj существенное;

•7 – если преимущество ui над uj явное;

•9 – если преимущество ui над uj абсолютное;

•2,4,6,8 – промежуточные сравнительные оценки:

2 – почти слабое преимущество, 4 – почти существенное пре-

имущество, 6 – почти явное преимущество и 8 – почти абсо- лютное преимущество.

Матрица парных сравнений является диагональной (aij = 1,i = 1, n) и обратно

пар строка × столбец заполняется нижний треугольник, а далее верхний уже автоматически − обратными значениями относительно диагонали.

Степени принадлежности принимают равными соответствующим координатам собственного вектора W = (w1, w2,..., wn)T матрицы парных сравнений А:

где λmax – максимальное собственное значение матрицы А.

Пример описания. Построить функцию принадлежности элемента нечеткого множества по терм-элементу «Высокий мужчина» на универсальном множестве {170, 175, 180, 185, 190,195}. Предположим, что известны такие парные сравнения:

53

•отсутствие преимущества 195 над 190;

•существенное преимущество 195 над 180;

•абсолютное преимущество 195 над 170;

•почти существенное преимущество 190 над 180;

•почти абсолютное преимущество 190 над 170;

•существенное преимущество 185 над 175;

•слабое преимущество 195 над 185;

•почти абсолютное преимущество 195 над 175;

•слабое преимущество 190 над 185;

•явное преимущество 190 над 175;

•почти существенное преимущество 185 над 180;

•почти явное преимущество 185 над 170;

•слабое преимущество 180 над 175;

•почти существенное преимущество 180 над 170;

•почти слабое преимущество 175 над 170.

Парные сравнения запишем следующей матрицей А:

Собственные значения матрицы парных сравнений А равны:

6,2494;

0,0318 + 1,2230i;

0,0318–1,2230i;

–0,1567 + 0,2392i;

–0,1567–0,2392i;

0,0004.

Следовательно, λmax = 6,2494 . Степени принадлежности, найденные по формулам (6.2) и (6.1), приведены в табл. 2. Нечеткое множество получилось субнормальным. Для его нормализации разделим все степени принадлежности на максимальное значение, т.е. на 0,3494. Графики функций принадлежности субнормального и нормального нечетких множеств «высокий мужчина» изображены на рис. 11. Разница между λmax и n служит мерой несогласованности парных

54

Пример программы. Вектор собственных чисел матрицы А и макси-

мальное собственное значение:

Wλ := eigenvals (A)

0.032 + 1.223i

0.032 − 1.223i

Далее объявляется блок Given с начальными условиями значения весов w. В блоке система из двух уравнений. Блок завершается ко- мандой решения Find(). После решения системы уравнений делается

переход от субнормального нечеткого s множества к нормальному :

55

Решение изображено на рис. 11.

Практическое задание: в качестве персонального задания придумайте терм-элемент и согласуйте его вариант с преподавателем.

Содержание задания: сформировать критерии парных сравнений и построить ФП терм-элемента методом парных сравнений, решив систему (6.2). Составьте алгоритм решения уравнения для Mathcad.

Результат практики: матрица парных сравнений по шкале Саати и функция принадлежности, полученная по данным матрицы. Функцию представить графически как субнормальную и нормированную (см. рис. 11).

Рис. 11. Синтезируемые функции принадлежности нечеткого множества «высокий мужчина»; I − субнормальная; II − нормированная

Справка к алгоритму: вектор собственных чисел матрицы парных сравнений А рассчитается функцией eigenvals(A), где максимальное значение является первым элементом вектора возвращаемых функцией значений. Далее можно уже решать систему уравнений (6.2), используя блок Given/ Find.

Контрольные вопросы

1.Парные сравнения – методика коллективная или персональная.

2.Назовите основные вычислительные трудности алгоритма парных сравнений при его реализации на ЭВМ.

3.Как вы понимаете смысл нормирования полученных ФП?

6.2. Синтез нечетких правил на основе горного алгоритма

Теория. Обозначим через V1,V2,..., Vc центры кластеров, найденные в результате горной кластеризации. Для упрощения выкладок примем, что центры

56

кластеров заданы двумя координатами Vi = (xi , yi ),i = 1,c . Задача состоит в синтезе нечетких правил, связывающих вход (х) с выходом (у).

Каждому i-му центру кластера Vi (i = 1,c) ставится в соответствие одно не-

четкое правило:

yi». Функции принадлежностей этих нечетких термов задаются гауссовой кривой:

где β – параметр алгоритма горной кластеризации.

Пример программы. Генерируем пространство признаков X в две ко-

ординаты и отдельно уровни-потенциалы кандидатов-центров Z:

Центры кандидаты и выбранные изображены на рис. 12.

Рис. 12. Координатное пространство Х признаков;

Z1 − назначенные кандидаты; Z2 − выбранные по алгоритму центры; количество выбранных центров − Nf = 2

57

Решение по выражению (6.3)

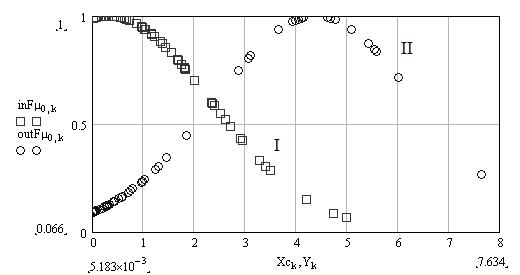
изображено графически на рис. 13.

по отношению к первому центру кластеризации;

I − ФП входа (антецедент); II ФП выхода (консеквент)

Составим смысловую интерпретацию результата. Исходные данные – вектора универсумов: Х – входной сигнал; Y – выходной сигнал. По начальным условиям горного алгоритма из координатного пространства

{X,Y} было определено 2 центра кластеров, что соответствует задаче построения базы правил из двух правил. Приведение к нечеткости X и Y было произведено по выражению (6.3). Причем X метрически взаимо-

действовал с 1-ми координатами кластеров, а Y со 2-ми, т.к. раз-

мерность кластерного пространства {X,Y} соответствует числу векто-

ров универсума. Таким образом, было сформировано два правила (ин-

декс j) согласно числу центров с двумя векторами inFµ и двумя outF

– функциями принадлежности подусловия и подзаключения для каждого из правил. Рассмотренный прием не только синтезирует ФП, но и их табличное отношение – базу правил.

58

Практическое задание: произвести синтез нечетких правил, связывающих вход и выход ФП, полученных по (6.3) в результате решения горной кластеризации.

Содержание задания: использовать горный алгоритм, полученный по результатам практики 5.3. Для выполнения задания в алгоритме должно быть просчитано не менее 3-х итераций или организованы циклические итерации с заданной точностью решения (не более 0.01). Сгенерировать координатное пространство и центры-кандидаты, используя пример. Размерность и способ случайной генерации могут отличаться. Рассчитать ФП по выражениям (6.3).

Результат практики: графики ФП входа и выхода синтезированного 1-го правила для 1-го центра. Для более полного выполнения задания желательно представить базу знаний из трех правил и более.

Контрольные вопросы

1.Объясните смысл результата горного алгоритма для алгоритмов синтеза нечетких правил.

2.Сравните трудность алгоритма и степень его автоматизации в получении результата с алгоритмом синтеза предыдущего раздела 6.1.

3.Как вы понимаете систему «вход-выход» на основании логического пра-

вила.

6.3. Синтез нечетких правил на основе нечеткой кластеризации

Теория. Нечеткие правила можно синтезировать по результатам нечеткой кластеризации. Например, пусть объекты кластеризации имеют два признака ( n = 2 ).Тогда результаты нечеткого разбиения можно представить трехмерной поверхностью. Для построения такой поверхности следует для каждого объекта отложить по осям абсцисс и ординат значения признаков, а по оси аппликат – степень принадлежности объекта нечеткому кластеру. Количество поверхностей равно числу кластеров (n), так как каждый объект принадлежит всем центрам, но с разной степенью принадлежности. Таким образом, каждая принадлежность объекта будет иметь отношение к отдельной плоскости. При синтезе каждому кластеру можно поставить в соответствие одно нечеткое правило.

По результатам нечеткой кластеризации можно синтезировать нечеткие правила различных баз знаний: синглтонной, Мамдани и Сугено [7]. Функции принадлежности термов в посылках правила получают проецированием степеней принадлежности соответствующего кластера (строчек матрицы нечеткого разбиения F) на оси входных переменных. Затем полученные множества степеней принадлежностей аппроксимируют подходящими параметрическими

59

функциями принадлежности1. При нечеткой кластеризации каждый объект может принадлежать всем кластерам, но с разной степенью. Если объект описы-

вается только одним признаком, тогда предлагается сопоставить нечеткий кластер нечеткому множеству. При этом функция принадлежности нечетко- го кластера будет соответствовать искомой функции принадлежности не-

четкого множества. Это очень важное условие, особенно при проведении эксперимента со случайными значениями. Можно в альтернативу статистической обработки синтезировать решение о нечетком значении среднего (один кластер), а также о значении наблюдений на n-интервалах (n-кластеров). К данному варианту обработки измерений относятся нижеследующие пример и задание.

По условиям задачи объекты задаются числовыми значениями, следовательно, нечеткое множество надо рассматривать как нечеткое число. Поэтому для обеспечения свойств нормальности и выпуклости найденные нечеткие множества нужно аппроксимировать параметрическими функциями принадлежности.

Пример описания является классическим для учебных задач. Пусть задана обработка данных более 300 измерений терма «Временя разгона автомобиля» с места до скорости 60 км/ч. По распределению этих данным стоятся три функции принадлежности. Результатом выполнения синтеза ФП правил являются нечеткие множества, которые можно интерпретировать как терм-элементы «Малое», «Среднее» и «Значительное» время разгона. Число терм-элементов можно регулировать числом задаваемых кластеров.

MC:= FCL(X, c, Iter, ε, m)

Fn := MC0 - Матрица принадлежностей кластерам

V:= MC1 - Координаты центров

1 Например L-R функциями или гауссовой кривой, см. разд.8. Это же условие получения ФП для дальнейших действий в системах нечеткого вывода распространяется и на синтез горным алгоритмом.

60