2012

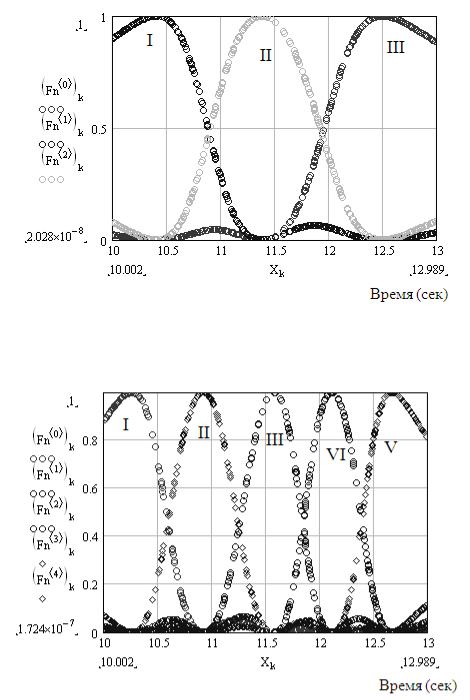
Результат приведен на рис.14., для с:=5 на рис. 15. Шкала уни-

версума отображает время разгона, а ФП имеют модальное значение в районе среднего значения экспертного знания о степени разгона для данной серии опытов.

Описание функции FCL() и ее параметров см. п.5.1., но в работе рекомендуется использование 3-х итераций, ранее выполненных в за-

дании 5.1.

Рис.14. Результат кластеризации – синтез 3-х элементов терма «Время разгона»: I − «Малое»; II − «Среднее»; III − «Большое»

Рис. 15. Результат кластеризации – синтез 5-ти элементов терма «Время разгона»: I − «Малое»; II − «Меньше среднего»; III − «Среднее»; IV − «Больше среднего»; V − «Большое»

61

Практическое задание: придумайте и согласуйте с преподавателем собственный вариант моделирования распределений по примеру времени разгона автомобиля. Синтезировать ФП по результату смоделированных стохастических распределений проводимых измерений. Содержание задания будет излагаться по примеру времени разгона автомобиля.

Содержание задания:

а) откройте ранее выполненный файл практики с алгоритмом нечетких c- средних. Назначьте числу объектов N значение от 40 до 50 и проследите, чтобы в тексте программы было не менее 3-х итераций;

б) перед началом 1-й итерации сгенерируйте одномерный вектор размерностью N. Вектор имитирует измерения разгона по времени в секундах. Поэтому назначайте в цикле каждому элементу среднее время, например, 12-15 сек. Далее прибавляете к этому значению случайное число, например rnd(3), для эмуляции вариаций (случайности) измерений в реальном эксперименте. Задайте число центров кластеров с:=3.

Результат практики: получите таблицу нечетких принадлежностей Fn. Отобразите на одном графике все три нечетких числа, значения которых находятся в колонках таблицы Fn. Положительный результат выполнения задания – это аналогия полученных графиков с рис. 14. Для большей достоверности результата можно добавлять итерации расчета Fn.

Контрольные вопросы

1.В чем важность в экспериментальной практике одномерных измерений? Какой дисциплине в данном случае составляет альтернативу технология синтеза правил?

2.Какие элементы матрицы принадлежностей определяют ФП и от чего зависит число синтезируемых правил по данным нечеткой кластеризации?

3.Какое основное алгоритмическое преимущество данного способа синтеза правил можно отметить по сравнению с предыдущими методами (п. 6.1 –

6.2).

62

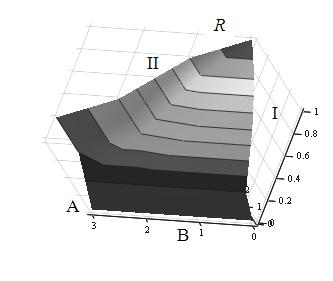
Рис. 16. Поверхность R − композиционное правило, формула знаний, связывающая вход-предусловие и выход-подзаключение;

I − проекция ФП входа; II − проекция ФП выхода

Далее, с использованием результата min-композиции R, осуществ-

ляются два способа расчета отклика (нечеткого вывода) по воздейст-

вию ФП, обозначенной как нечеткое множество С:

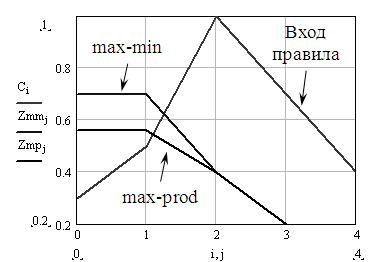
Решение демонстрируется графически на рис 17.

Практическое задание: решить матрицу R по min композиции на ФП предусловия и подзаключения; исследовать реакцию на нечеткое воздействие для полученной системы.

Содержание задания:

−открыть файл предыдущей работы построения ФП парными сравнениями;

−присвойте значение нормальной ФП входной переменной С;

−получите от преподавателя персональный вариант ФП входа X и выхода Y;

64

−составьте передаточное правило системы путем определения нечеткого отношения пар R = X o Y (применять в качестве t-нормы операцию min), при этом число строк R (размерность входа) должно быть равно размерности вектора C;

−решить задачу нечеткого вывода C o R типа max-min композиции с R, используя С в качестве входного вектора;

−сделать копию процедуры композиции и модифицировать ее под решение по max-prod. Присвоить значение новой выходной переменной и сравнить графически с предыдущим выводом.

Все этапы задания сопровождаются приведенным примером.

Результат практики: на одном графике отобразить значения входа − вектор С и значение ФП результатов нечеткого логического вывода (по примеру рис. 17).

Рис. 17. Два способа решения по композиционному правилу: выход по max-min и по max-prod композиции

Контрольные вопросы

1.Какую базовую числовую конструкцию в формуле классического вывода образуют элементы правила «ЕСЛИ ТО»?

2.Есть ли разница в чувствительности системы к входному воздействию при его обработке по max-min или max-prod композиции?

3.Какому типу систем эквивалентен базовый нечеткий вывод (статика, динамика)? Ответ обоснуйте с использованием характеристик, применяемых в расчетах числовых конструкций вывода.

65

8. АППРОКСИМАЦИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ ПАРАМЕТРИЧЕСКИМИ ФУНКЦИЯМИ

После процедуры синтеза ФП формально вы получаете только вектор из нечетких принадлежностей, но нет аналитической формулы самой функции. В технологиях, использующих расчеты с ФП, обычно ФП геометрически аппроксимируются гауссовыми функциями, которые имеют различные выражения и число параметров. В программном примере для данного раздела, кроме гауссовой аппроксимации, были дополнительно использованы две базовые формулы (L-R) функций для получения более точного результата аппроксимации ФП.

Теория. Для нахождения параметров нужно решить систему нелинейных уравнений, результат решения которых минимизирует квадратичный критерий (квадратичный функционал) невязки полученной ФП и рассчитываемой гауссовой кривой.

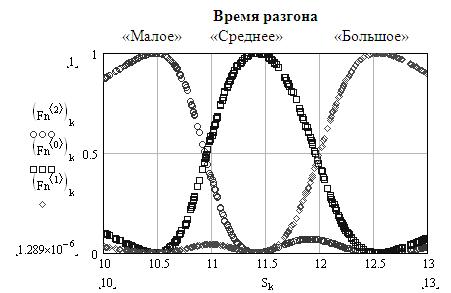
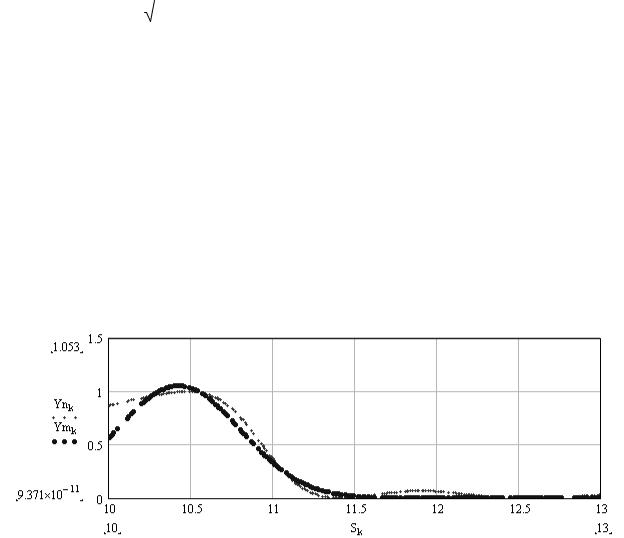
Пример программы. Объектом аппроксимации выберем результат не-

четкой кластеризации − ФП времени разгона автомобиля (п. 6.3); Fn

матрица результата кластеризации; Sk координата времени разгона

(рис. 18).

Рис. 18. Объекты аппроксимации по результатам нечеткой кластеризации

Демонстрируется решение аппроксимации «Скорость малая» (время разгона «Малое») по формуле закона нормального распределения

(функция F).

Задаются:

-квадратичный критерий SSE();

-начальные значения параметров a и b.

66

Далее решается нелинейное уравнение SEE() минимизации квадратов отклонения оператором Minerr() в блоке Given. Результат решения – это параметры a и b, указывающие соответственно крутизну склона функции и центр ее симметрии (рис. 19).

a = 0.379 b = 10.423

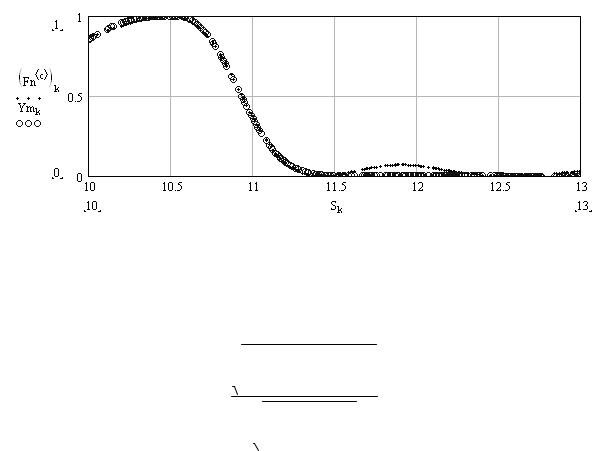
Рис. 19. Аппроксимация L-R функции;

тонкая линия — аппроксимируемая функция, утолщенная линия − результат аппроксимации

Приводим альтернативный блок расчетов аппроксимации ФП L-R-

функциями. Время расчетов значительно возрастает, но точность уве-

личивается (рис. 20).

67

a := 11.5 p := 2 α := 0.7 β := 0.7

SSE(a , α , β , p) := ∑(Ynk − F(Sk , a , α , β , p))2

k

Given

SSE(a , α , β , p) 0

Рис. 20. Улучшенная L-R аппроксимация, но с большим объемом вычислений

Сравнительный тест алгоритмов:

по формуле

∑ (Fn c ) − Ym 2

100

∑ ((Fn c ))2

68

произведены расчеты относительной погрешности аппроксимации ФП для трех типов скоростей разгона. Результат приведен в табл. 3.

Практическое задание: выполнить аппроксимацию функций принадлежностей параметрическими гауссовыми функциями.

Содержание задания: открыть файл с результатом нечеткой кластеризации, например по измерениям времени разгона автомобиля (п. 6.3). Выбрать вектор одной и полученной функций и, используя пример программы, найти параметры гауссовой функции, аппроксимирующей ФП. В качестве функции приближения выберите по желанию любую гауссову формулу.

Результат практики: изображения аппроксимации, аналогичные изображению результата на рис. 19 – 20.

Контрольные вопросы

1.В чем практическая ценность в получении формулы ФП разработчиком нечетких систем?

2.Связь числа параметров функции с точностью и скоростью вычислений.

3.Какие еще методы анализа способны выполнять подобную задачу аппроксимации?

69

9.УПРАВЛЕНИЕ И ПРИНЯТИЕ РЕШЕНИЙ В РАЗВИТИИ ТЕХНИЧЕСКИХ СИСТЕМ НА ОСНОВЕ НЕЧЕТКИХ МНОЖЕСТВ

9.1.Оценка риска модернизации технических систем в задачах содействия принятию решения

Теория. Основополагающим понятием в технике является понятие «техническая система». Т е х н и ч е с к а я с и с т е м а – это целостное образование, состоящее из взаимодействующих (взаимосвязанных) компонентов и обладающее свойствами, которые не сводятся к свойствам этих компонентов и не выводятся из них.

Техническая система (ТС) не может существовать как обособленный объект, без каких-либо связей с другими объектами. Она взаимодействует с внешней средой, характеризующейся конкретными объектами и определенной природой, может развиваться в этой среде и представляет собой открытое образование, состоящее из конечного множества подсистем и элементов с непосредственными или опосредованными связями.

ТС можно классифицировать по трем основным разделам: как системно-

структурное образование, как объект функционирования и как объект разви-

тия. Данная классификация требует введения ряда определений, связанных с понятиями ТС и ее жизненного цикла (ЖЦ).

К о н с т р у к ц и я Т С – представление (отображение или прообраз) упорядоченной в пространстве совокупности механически связанных между собой элементов ТС и представление допустимых строений (структур, признаков и параметров) каждого из этих элементов.

Э л е м е н т Т С – некоторый объект (материальный, энергетический, информационный), обладающий рядом свойств, обеспечивающих выполнение некоторых функций, внутреннее строение которого для целей исследования не представляет интереса.

Связью между элементами называется процесс их взаимодействия, важный для целей исследования.

С учетом последних двух определений ТС называется совокупность элементов со связями и целью функционирования, отличной от целей функционирования составляющих ее элементов.

Большой ТС называется система, состоящая из большого числа однотипных (однородных) элементов с однотипными связями.

70