
2012
.pdf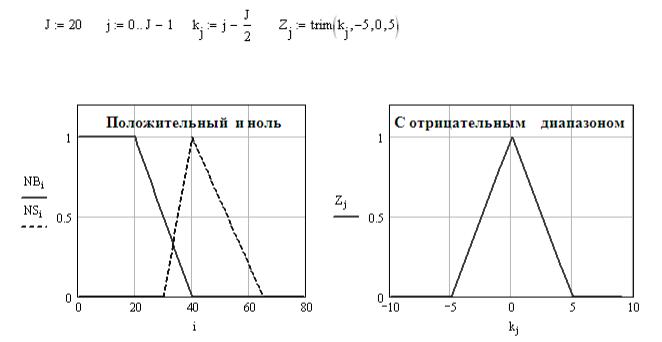
Результат построения ФП изображен на рис. 2.
Рис. 2. Примеры универсумов кусочно-линейных ФП
Обратите внимание, как формы ФП на рис. 2 могут выражать экс-
пертные знания. В простейшем случае интерпретации нечетких значе-
ний − это выражение нечетких чисел. Например «Нечеткое 40», «нечет-
кий 0». Лингвистическая интерпретация звучит, например, так:
«Температура ниже среднего» (трапеция); «температура выше средне-
го» (первый треугольник); «Нулевая температура» (второй треуголь-
ник).
Практическое задание: выполнить алгоритмы построения формул экспертных функций принадлежности.
Содержание задания: освоить практику создания, программирования и отладки процедур средствами Mathcad. В качестве примера процедуры описать операторами Mathcad функции trim и trap по формулам (2.1) и (2.2).
Результат практики: отлаженные процедуры trim и trap с демонстрацией их вызова с результатом графического построения ФП (рис. 2).
Контрольные вопросы
1.Назовите причину, по которой кусочно-линейные функции стали основными для экспертных представлений знаний.
2.Охарактеризуйте смысловую разницу одного и того же экспертного понятия, выраженного треугольником и трапецией.
3.Перечислите требования к кусочно-линейным функциям, сформированных в качестве входных данных для расчетов и моделирования. Возможна ли мультимодальность ФП в отражении экспертного мнения?
11

3. НЕЧЕТКИЕ ОБОБЩЕНИЯ НА ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Несмотря на то, что ФП конкретная числовая функция, формально представляющая элемент нечеткого множества (способна к употреблению в численных алгоритмах), самого понятия функции, как биекции, в теории нечетких множеств нет. Нет изоморфизма относительно определенных свойств, нет пространственных конструкций с топологическими и метрическими свойствами, а значит, нет сходимости и однозначности проводимых операций, нет доказательства теорем на основе математической дедукции. Отсутствие единственности решения и способности дедуктивно развиваться теория нечетких множеств замещает другим своим фундаментальным свойством − неоднозначным обоб- щением четких отношений, отображений, операций, алгебраических множественных конструкций и т.п. В общем, нечеткая теория обладает тем, что называется интуиция в интеллектуальном сознании при поиске решения без предварительной подготовки всей совокупности исходных формальных данных. Нужно понимать, что обобщения (нечеткость) и однозначная биекция (изоморфизм) − взаимоисключающие понятия, одновременное положительное упоминание этих понятий в одной теории будет являться системной ошибкой.
Данный раздел представляет особенности нечетких обобщений на примере нечетких операторов, группа которых получила название s-нормы для обобщений четкой логической операции ИЛИ и группы t-нормы – для операции И.
3.1. Нечеткие операторы
Теория. Рассмотрим примеры нечетких логических операций на нечетких множествах A и B, заданных на одном и том же универсуме X.
Операторы t-нормы.
Логическая конъюнкция (пересечение) Τ( A B) = min{Τ( A),Τ(B)}
Альтернативные формулы
Алгебраическое произведение Граничное произведение
Драстическое произведение
Τ( A B) = (Τ( A) Τ(B))
Τ( A B) = max{Τ( A) + Τ(B) − 1,0}
Τ(B), |
если Τ( A) = 1 |
|
|
|
если Τ(B) = 1 |
Τ( A B) = Τ( A), |
||
|
0, |
иначе |
|
||
Операторы s-нормы.
12

Логическая дизъюнкция (объединение) |
Τ( A B) = max{Τ( A),Τ(B)} |
|
Альтернативные |
формулы |
|
Алгебраическая сумма |
Τ( A B) = (Τ( A) + Τ(B) − Τ( A) Τ(B)) |
|
(треугольная s-норма) |
|
|
Граничная сумма |
Τ( A B) = min{Τ( A) + Τ(B),1} |
|
Драстическая сумма |
Τ(B), |
если Τ( A) = 0 |
|
|
если Τ(B) = 0 |
|
Τ( A B) Τ( A), |
|
|
|
иначе |
|
1, |
|
Пример программы. Пакет Mathcad имеет операторы max() и min(),
в качестве аргументов использующие числовые перечисления, векторы и двумерные матрицы. Соответственно построение логических операто- ров не вызывает никаких затруднений.
Задаем ФП:
Ai := trap(i, 0, 10, 20, 50) |
Bi := trim(i, 20, 40, 65) |
Объединение: |
Пересечение: |
Ci := max( Ai, Bi) |
Ci := min( Ai, Bi) |
Это пример логического взаимодействия двух ФП на одном универ- суме, объявленного ранжированной переменной i.
Практическое задание: научиться находить результат нечетких логических операций на основании неоднозначных обобщений.
Содержание задания: объявите универсум в форме ранжированной переменной. Постройте две исходные функции одной размерности. Используя основные и альтернативные формулы раздела «Теория», получите функцию принадлежности результата.
Результат практики: графическая демонстрация результирующих ФП как результат нечетких логических операций.
Контрольные вопросы
1.В чем выражается обобщение теории нечетких множеств по отношению к логическим операциям?
2.Как вы понимаете геометрический смысл операций max и min для конкретных элементов нечетких множеств?
3.Проанализируйте формулы операторов t- и s-нормы и определите, какие будут более чувствительными и точными к изменению операндов?
3.2.Нечеткая импликация
Теория. Нечеткой импликацией или просто − импликацией нечетких вы-
сказываний A и B (записывается как: A B и читается − «ИЗ A СЛЕДУЕТ
13
B », «ЕСЛИ A , ТО B ») называется бинарная логическая операция, результатом которой является нечеткое высказывание. Нечеткая импликация играет ключевую роль как элементарный вывод в процессе нечетких логических рас- суждений. Так же, как и в математической логике, первый ее операнд (нечеткое высказывание) называется посылкой или антецедентом, а второй − заключени- ем или консеквентом. В математике импликации – двигатель дедукции, приводят к заключениям о необходимости и достаточности условий, доказательствам теорем, лемм и их следствий. В нечетких технологиях импликации образуют многомерную систему подзаключений для ее дальнейшего агрегирования (композиционного объединения) в единственную формулу нечеткого вывода, кото-
рая называется новой формой знания.
Пример описания. Нечеткие обобщения импликации могут принимать значения, определяемые по одной из следующих формул.
• Классическая нечеткая импликация, предложенная JI. Заде:
T ( A B) = max{min{T ( A),T (B),},1 − T ( A)}.
Эту форму нечеткой импликации называют также нечеткой импликаци-
ей Заде.
• Классическая нечеткая импликация для случая T ( A) ≥ T (B) :
T ( A B) = max{T (− A),T (B)}= max{1 − T ( A),T (B)}.
Эту форму нечеткой импликации иногда называют нечеткой имплика-
цией Гёделя.
• Нечеткая импликация, предложенная Э. Мамдани:
T ( A B) = min{T ( A),T (B)}.
Эту форму нечеткой импликации также называют нечеткой импликаци-
ей Мамдани или нечеткой импликацией минимума корреляции. Можно заметить, что в случае T ( A) ≥ 0.5 и T (B) ≥ 0.5 классическая нечеткая импликация превращается в нечеткую импликацию Мамдани.
• Нечеткая импликация, предложенная Я. Лукасевичем:
T ( A B) = min{1,1 − T ( A) + T (B)}.
Эту форму нечеткой импликации также называют нечеткой импликаци-
ей Лукасевича.
• Нечеткая импликация, предложенная Дж. Гогеном:
T ( A B) = min{1,T (B) /T ( A)}, где T ( A) > 0.
Эту форму нечеткой импликации также называют нечеткой импликаци-
ей Гогена.
14
•Нечеткая импликация по формуле граничной суммы:
T ( A B) = min{1,T ( A) + T (B)}.
•Нечеткая импликация по формуле произведения:
T ( A B) = {T ( A) T (B)}
•Нечеткая импликация, предложенная Н. Вади:
T ( A B) = max{T ( A) T (B),1 − T ( A)}.
•Нечеткая импликация Брауэра:
|
1, |
если T ( A) ≤ T (B) |
T ( A B) = |
|
иначе |
T (B), |
||
Эта форма нечеткой импликации получила свое название в честь голландского логика JI. Брауэра (1881—1966), основоположника математического интуиционизма.
• Нечеткая импликация стандартной логики последовательностей (R-SEQ):
1, если T ( A) ≤ T (B)
T ( A B) =
0, иначе
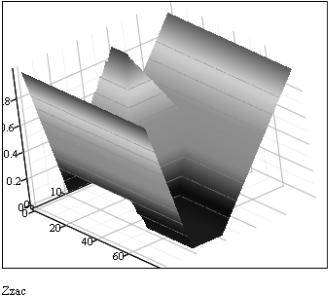
Пример программы. Импликация по Л. Заде (рис. 3).
Zmi, j := min(µCj, µAi)
µAi := trap(i, 0, 10, 20, 50)
Zzaci, j := max(min(µCj, µAi), 1 − µA j)
Рис. 3. Поверхность нечеткого вывода по импликации Л. Заде
15
Практическое задание: выполнить решение по базовым примерам нечеткой импликации.
Содержание задания: обратите внимание на двумерную размерность импликации. Это результат участия в решении ФП различной размерности. Объявите две функции с аргументами по ранжированным переменным разной размерности. Выполнить импликации, отличные от примера, используя формулы раздела «Теория».
Результат практики: графические построения поверхностей нечетких импликаций.
Контрольные вопросы
1.Приведите таблицу истинности для четкой операции импликации.
2.Обладает ли предметной наглядностью поверхность вывода нечеткой импликации?
3.Постройте простейшую сеть импликаций на отношениях направленного графа. К какой системе можно отнести данную конструкцию: накопление знаний, обработка знаний, система вывода? Предложите собственный вариант ответа.
3.3. Композиция бинарных нечетких отношений
Теория. Пусть Q и R — конечные или бесконечные бинарные нечеткие отношения. Причем нечеткое отношение Q = { xi , x j ,µQ ( xi , x j )} задано на де-
картовом произведении универсумов X 1 × X 2 , а нечеткое отношение R = { x j , xk , µ R ( x j , xk )}— на декартовом произведении универсумов X 2 × X 3 .
П р и м е ч а н и е . Следует понимать, что, например, Q это матрица результата композиции, состоит из коэффициентов нечетких принадлежностей и
имеет размерность в i строк и j столбцов. |
|
|
К о м п о з и ц и я |
д в у х б и н а р н ы х н е ч е т к и х отношений. Нечет- |
|
кое бинарное отношение, заданное на декартовом произведении X 1 × X 3 |
и обо- |
|
значаемое черезQ R , называется композицией бинарных нечетких отношений |
||
Q и R, а его функция принадлежности определяется следующим выражением: |
||
µQ R ( xi |
, xk ) = max{min{µQ ( xi , x j ),µ R ( x j , xk )}} |
(3.1) |
|
x j X 2 |
|
( xi , xk X 1 × X 3 ).
Обратите внимание, что в результирующей матрице композиции сокращена размерность j. Определенную таким образом композицию бинарных нечет-
16
ких отношений называют иногда max− min -композицией или максиминной сверткой нечетких отношений.
Пример описания.
• Max-min-композиция или максиминная нечеткая свертка:
µβ (y) = max{min{µΑ (x), µQ ( x, y )}}.
x X
• Max-prod-композиция:
µβ (y ) = max{µ Α (x) µQ ( x, y )}.
x X
• Min-max-композиция:
µβ (y ) = min{max{µΑ (x),µQ ( x, y )}}.
x X
• Max-max-композиция:
µβ (y ) = max{max{µΑ (x),µQ ( x, y )}}.
x X
• Min-min-композиция:
µβ (y ) = min{min{µΑ (x),µQ ( x, y )}}.
x X
• Max-average-композиция:
µβ (y ) = 0.5 max{µ Α (x) + µQ ( x, y )}.
x X
• Sum-prod-композиция:
µβ (y ) = f (∑ (µ Α (x) µQ ( x, y ))),
x X
где f — некоторая логистическая функция типа сигмоидной, которая ограничивает значения функции числом из интервала [0, 1]. Этот метод композиции применяется в приложениях искусственных нейронных сетей для установления взаимосвязей между параллельными слоями в многослойных сетях.
Пример программы. Пример программы содержит входные данные: матри-
цы нечетких принадлежностей Ms и Mt, на основании которых осущест-
вляется нечеткая композиция. Матрица Ms – нечеткое описание при-
надлежности психологических характеристик к профессиям. Матрица Mt
– принадлежность психологических характеристик к конкретным участ-
никам теста на профпригодность. Матрицы, например, могут быть со-
ставлены экспертами-психологами или получены как результат работы некоторого алгоритма обработки нечетких данных. Смысл выполняемого примера – это получение матричного отношения принадлежностей про-
фессий и кандидатов с последующим сокращением размерности психоло-
гических характеристик.
Первая матрица Ms. Нечеткое отношение профилирования специаль-
ностей обучения.
17

0.9 |
0.9 |
0.8 |
0.4 |
0.5 |
0.3 |
0.6 |
0.2 |
0.9 |
0.8 |
||
|
0.8 |
0.5 |
0.9 |
0.3 |
0.1 |
0.2 |
0.2 |
0.2 |
0.5 |
0.5 |
|
|
|
||||||||||
Ms := 0.3 |
0.9 |
0.6 |
0.5 |
0.9 |
0.8 |
0.9 |
0.8 |
0.6 |
0.3 |
||
|
0.5 |
0.4 |
0.5 |
0.5 |
0.2 |
0.2 |
0.3 |
0.3 |
0.9 |
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.7 |
0.8 |
0.8 |
0.2 |
0.6 |
0.2 |
0.2 |
0.3 |
0.3 |
0.2 |
||
Табличная расшифровка матрицы Ms:
|
Быстротаи |
Умение |
Устойчивость и |
Зрительная |
Быстрота |
|
гибкость |
быстро |
концентрация |
память |
реакции |
|
мышления |
принимать |
внимания |
|
|
|
|
решения |
|
|
|
|
|
|
|
|
|
Менеджер |
0.9 |
0.9 |
0.8 |
0.4 |
0.5 |
|
|
|
|
|
|
Программист |
0.8 |
0.5 |
0.9 |
0.3 |
0.1 |
|
|
|
|
|
|
Водитель |
0.3 |
0.9 |
0.6 |
0.5 |
0.9 |
|
|
|
|
|
|
Секретарь |
0.5 |
0.4 |
0.5 |
0.5 |
0.2 |
|
|
|
|
|
|
Переводчик |
0.7 |
0.8 |
0.8 |
0.2 |
0.6 |
|
|
|
|
|
|
|
Двигательная |
Физ.выно- |
Координация |
Эмоционально- |
Ответст- |
|
память |
сливость |
движений |
волевая |
венность |
|
|
|
|
устойчивость |
|
|
|
|
|
|
|
Менеджер |
0.3 |
0.6 |
0.2 |
0.9 |
0.8 |
|
|
|
|
|
|
Программист |
0.2 |
0.2 |
0.2 |
0.5 |
0.5 |
|
|
|
|
|
|
Водитель |
0.8 |
0.9 |
0.8 |
0.6 |
0.3 |
|
|
|
|
|
|
Секретарь |
0.2 |
0.3 |
0.3 |
0.9 |
0.8 |
|
|
|
|
|
|
Переводчик |
0.2 |
0.2 |
0.3 |
0.3 |
0.2 |
|
|
|
|
|
|
Вторая матрица Mt. Нечеткое отношение профилирования кандида-
тов на обучение.
|
0.9 |
0.8 |
0.7 |
0.9 |
1 |
|
|
|
|
0.6 |
0.4 |
0.8 |
0.5 |
0.6 |
|
|
|
|
|||||
|
0.5 |
0.2 |
0.3 |
0.8 |
0.7 |
|
|
|
|
0.5 |
0.9 |
0.5 |
0.8 |
0.4 |
|
|
|
|
|
|
|
|
|
Mt := |
|
1 |
0.6 |
0.5 |
0.7 |
0.4 |
|
|
0.4 |
0.5 |
1 |
0.7 |
0.8 |
|
|
|
|
0.5 |
0.8 |
0.9 |
0.5 |
0.4 |
|
|
|
|
|||||
|
0.5 |
0.6 |
0.7 |
0.6 |
0.5 |
|
|
|
|
0.8 |
1 |
0.2 |
0.5 |
0.6 |
|
|
|
|
|||||
|
0.3 |
0.5 |
0.9 |
0.6 |
0.8 |
|
|
Табличная расшифровка матрицы Mt:
18

|
|
Петров |
Иванов |
|
Сидоров |
Васильева |
Григорьева |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Быстрота и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гибкость |
0.9 |
|
|
|
0.8 |
|
0.7 |
|
0.9 |
1 |
||||
|
мышления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умение быстро прини- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мать решения |
0.6 |
|
|
|
0.4 |
|
0.8 |
|
0.5 |
0.6 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Устойчивость и концен- |
0.5 |
|
|
|
0.2 |
|
0.3 |
|
0.8 |
0.7 |
||||
|
трация внимания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Зрительная память |
0.5 |
|
|
|
0.9 |
|
0.5 |
|
0.8 |
0.4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Петров |
Иванов |
|
Сидоров |
Васильева |
Григорьева |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Быстрота реакции |
1 |
|
|
|
0.6 |
|
0.5 |
|
0.7 |
0.4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двигательная память |
0.4 |
|
|
|
0.5 |
|
|
1 |
|
0.7 |
0.8 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Физическая выносли- |
0.5 |
|
|
|
0.8 |
|
0.9 |
|
0.5 |
0.4 |
||||
|
вость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координация движений |
0.5 |
|
|
|
0.6 |
|
0.7 |
|
0.6 |
0.5 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эмоционально-волевая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
устойчивость |
0.8 |
|
|
|
1 |
|
|
0.2 |
|
0.5 |
0.6 |
|||
|
Ответственность |
0.3 |
|
|
|
0.5 |
|
0.9 |
|
0.6 |
0.8 |
||||
Процедура max− min -композиции: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
Rmaxmin ( M1 , M2 ) := |
|
K ← cols ( M1 ) − 1 |
|
|
|
|
|
|
||||||
|
|
|
|
I ← rows ( M1 ) − 1 |
|
|
|
|
|
|
|||||
|
|
|
|
J ← cols ( M2 ) − 1 |
|
|
|
|
|
|
|||||
|
|
|
|
for |
|
i 0 .. I |
|
|
|
|
|
|
|
||
|
|
|
|
for |
j 0 .. |
J |
|
|
|
|
|
|
|||
|
|
|
|
|
|
s ← 0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
for |
k 0 .. |
K |
|
|
|
|
|
||
|
|
|
|
|
|
s k ← min (M1 i , k , M2 k , j) |
|
||||||||
|
|
|
|
|
|
ri , j ← max ( s ) |
|
|
|
|
|
||||
|
|
|
|
return |
r |
|
|
|
|
|
|
|
|
|
|
Результат композиции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.9 |
0.9 |
|
0.8 |
0.9 |
0.9 |
|
|||||
|
|
|
|
|
0.8 |
0.8 |
|
0.7 |
0.8 |
0.8 |
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
Rmaxmin(Ms , Mt) = 0.9 |
0.8 |
|
0.9 |
0.7 |
0.8 |
|
|
|
||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
0.8 |
0.9 |
|
0.8 |
0.6 |
0.8 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0.7 |
0.7 |
|
0.8 |
0.8 |
0.7 |
|
|||||
изложен в табл. 1.
19

|
|
|
|
|
Таблица1 |
|
Таблицапринадлежностейпрофпригодности |
|
|||
|
|
|
|
|
|
|
Петров |
Иванов |
Сидоров |
Васильева |
Григорьева |
|
|
|
|
|
|
Менеджер |
0.9 |
0.9 |
0.8 |
0.9 |
0.9 |
|
|
|
|
|
|
Программист |
0.8 |
0.8 |
0.7 |
0.8 |
0.8 |
|
|
|
|
|
|
Водитель |
0.9 |
0.8 |
0.9 |
0.7 |
0.8 |
|
|
|
|
|
|
Секретарь |
0.8 |
09 |
0.8 |
0.6 |
0.8 |
|
|
|
|
|
|
Переводчик |
0.7 |
0.7 |
0.8 |
0.8 |
0.7 |
|
|
|
|
|
|
Практическое задание: получить навыки составления исходных условий, решения-вывода max− min и max− prod1 нечеткой композиции.
Содержание задания: самостоятельно разработать свой вариант исходных данных нечеткой композиции и согласовать его с преподавателем перед выполнением расчетов. Далее:
− запрограммировать процедуру композиции с входными параметрами из двух матриц, используя собственную методику построения кода или на основе процедуры примера. Для понятия формулы композиции приводится еще вари-
ант ее написания на языке |
логики 1-го |
порядка для композиции матриц |
Мs Мt: |
|
|
i, j ∑∑max( k ∑{v | vk |
:= min(Msi ,k , Mtk , j )}) ; |
|
i j |
k |
|
−отладить процедуру, используя в качестве входных данных матрицы Ms
иMt. В результате ответ должен совпасть с данными табл. 1;
−решить собственный вариант нечеткой композиции.
Результат практики: матрицы результата тестового примера и собственного варианта нечеткой композиции. Прокомментировать преподавателю смысловой результат композиции собственного варианта.
Контрольные вопросы
1.Каковы условия правильного соотношения размерностей матриц для операции композиции?
2.Можно ли решение по композиции отнести к системам снижения исходной размерности?
3.Является ли операция нечеткой композиции линейной для машинных алгоритмов? В чем ее основная машинная трудность?
1 Операция prod – замена нечеткой логической коньюнкции min на алгебраическое произведение prod.
20
