2012

X2k, i := if (Fn 0 )k ≤ (Fn 1 )k, Xk, i, 0

Результат демонстрируется графически на рис. 8.

Рис. 8. Смещение координат центров кластеризации образцовой «Бабочки» при коррекции расстояний центр-объект нормой Махаланобиса

Практическое задание: формирование корректирующих выражений для стандартной евклидовой нормы в алгоритмах кластерного анализа.

41

Содержание задания: формирование матриц диагональной1 и дисперсионной2 норм; коррекция кластерной классификации разработанными нормами.

Для выполнения задания используется ранее созданный файл с тремя итерациями нечеткой кластеризации. Сделайте копию файла, формируйте матрицы нормы соответствующей размерности используемого координатного пространства. Для этого скорректируйте алгоритм каждой итерации (шаг 4 алгоритма в разд. 5.2), добавляя матрицу B в формулу определения расстояния центр-объект (5.6) с результатом модификации нормы по выражению (5.10) (см. «Пример программы»).

Результат практики: сравнительная графическая демонстрация результата кластеризации со стандартной евклидовой нормой, нормой модифицированной диагонально и по Махаланобису (рис. 8).

Контрольные вопросы

1.Поясните значение нормы для линейных пространств, объекты применения нормы, что она обобщает?

2.Назовите примеры измерений в любой практической области деятельности, где по вашему усмотрению целесообразно применение диагональной нормы, нормы Махаланобиса?

3.Роль дисперсионных характеристик в изменении (коррекции) стандартной нормы, или в чем смысл учета вариаций по направлениям?

5.3. Горный алгоритм

Теория. Горный алгоритм кластеризации предложен Ягером (Yager) и Филевым (Filev) в 1993 г. Особенностью алгоритма является то, что он не требует задания количества кластеров. Зависимость числа кластеров от свойств координатного пространства объектов может задавать разработчик программы алгоритма. Алгоритм характеристически (четко) проводит кластеризацию. В нечетких технологиях это важное свойство алгоритма позволяет определять число кластеров, например в задачах синтеза знаний, где по информативной емкости координатного пространства требуется определение числа правил для экспертной базы знаний.

Пример описания. Детально понять алгоритм можно только при его программировании и отладке. Приводимая теория до раздела «Пример программы»

1 Диагональную норму можно рассматривать, например, как способ весовой коррекции отдельных направлений (координат) признаков.

2 В основе нормы Махаланобиса – обратные отношения входных дисперсий, корректирующие случайный разброс объектов кластеризации, точнее их координат.

42

в основном пошагово знакомит с метрическими и пространственными свойствами алгоритма.

На первом шаге горной кластеризации определяют точки, которые могут быть центрами кластеров. На втором шаге для каждой такой точки рассчитывается значение потенциала, показывающего возможность формирования кластера в ее окрестности. Чем гуще расположены объекты в окрестности прототипа кластера, тем выше значение его потенциала. На третьем шаге итерационно выбираются центры кластеров среди точек с максимальными потенциалами. Рассмотрим горный алгоритм кластеризации подробнее.

Н а п е р в о м ш а г е необходимо сформировать потенциальные центры кластеров. Для алгоритма горной кластеризации число потенциальных центров кластеров (Q) должно быть конечным. Такими центрами могут быть как объекты кластеризации (строчки матрицы X), так и особые точки факторного пространства. В последнем случае диапазоны изменения входных признаков разбивают на несколько интервалов. Проведя через точки разбиения прямые, параллельные координатным осям, получаем решеточный гиперкуб. Узлы этой решетки и будут соответствовать центрам потенциальных кластеров. Обозначим через qr – количество значений, которые могут принимать центры кластеров по r-й координате, r = 1, n . Тогда количество возможных кластеров будет

равно: Q = q1q2...qn.

Н а в т о р о м ш а г е алгоритма рассчитывается потенциал центров кластеров по следующей формуле:

P(Z h ) = ∑exp(-αD(Z h , X k )), h = 1,Q,

k =1,M

где Z h = (z1,h , z2,h ,..., zn,h )– потенциальный центр кластера h, h = 1,Q; α – положительная константа; D(Z h , X k ) – расстояние между потенциальным центром кластера (Zh) и объектом кластеризации (Xk). В евклидовом пространстве это расстояние рассчитывается по формуле:

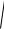
D(Z h , X k ) = Z h − X k 2 .

Когда объекты кластеризации заданы двумя признаками (n = 2), графическое изображение распределения потенциала будет представлять собой поверхность, напоминающую горный рельеф. Отсюда и название – горный алгоритм кластеризации.

Н а т р е т ь е м ш а г е алгоритма в качестве центров кластеров выбирают координаты «горных вершин». Центром первого кластера назначают точку с наибольшим потенциалом. Обычно наивысшая вершина окружена несколькими достаточно высокими пиками. Назначение центром следующего кластера точки

43

с максимальным потенциалом среди оставшихся вершин привело бы к выделению большого числа близко расположенных центров кластеров. Следовательно, перед выбором следующего кластерного центра необходимо исключить влияние только что найденного кластера. Для этого значение потенциала оставшихся возможных центров кластеров пересчитывается следующим образом: от текущих значений потенциала вычитают1 вклад центра только что найденного кластера (поэтому кластеризацию по этому методу иногда называют субтрактивной, от англ. subtractive – вычитание). Перерасчет потенциала происходит по формуле:

P2 (Z h ) = P1 (Z h ) − P1 (V1 ) exp(−βD(Z h ,V1 )), Z h ≠ V1 , h = 1,Q

Z1 ,Z 2 ,...,ZQ

Центр второго кластера определяется по максимальному значению обновленного потенциала:

V1 = agr max(P2 (Z 1), P2 (Z 2 ),..., P2 (ZQ )).

Z h :Z h ≠V1 ,h=1,Q

Затем снова пересчитывается значение потенциалов:

P3 (Z h ) = P2 (Z h ) − P2 (V2 ) exp(−βD(Z h ,V2 )), Z h ≠ V1 , h = 1,Q .

Итерационная процедура выделения центров кластеров продолжается до тех пор, пока максимальное значение потенциала превышает некоторый порог. Кластеризация по горному алгоритму не является нечеткой, однако ее часто используют при синтезе нечетких правил из данных.

Пример программы. Версия процедуры, которая из 2-мерного коор-

динатного пространства X формирует все возможные пары центров-

кандидатов. Результат - тоже координатное пространство, если про-

цент (порог от Рmax) малый процент. Если процент высокий - то из полного числа пар остается некоторое подмножество из тех же коор-

динат. Вывод: для координат данной и большей размерности достаточ-

но указать возможные их последовательности и будет выдан резуль-

тат отсортированных по порядку центров.

Начальные условия, включая генерацию координатного пространст-

ва Х:

1 Найденный максимальный потенциал своими координатами обозначает новый центр кластеризации. Для расчета координат следующего центра текущий максимальный потенциал исключается из кандидатов (обнуляется ), а пространство соседних потенциалов уменьшается в экспоненциальной зависимости от центра кластера – чем дальше от центра, тем больше экспоненциальный распад делителя потенциалов. Таким образом, ослабляется влияние значимых потенциалов вокруг лидера – центра кластеризации, повышая шансы новых потенциалов стать центрами, но уже на периферии пространства признаков от заданного центра.

44

Генерируем пространство признаков в 2 координаты

CentrClaster(). Функция горной кластеризации CentrClaster() полно-

стью описывается в приложении 2. Входные параметры: X − координаты объектов; α, β, − экспоненциальные веса; процент потенциала (в при-

мере 55%) от максимального, который будет учитываться при расчете вершин, если остаются вершины ниже указанного процентного отноше-

ния, то алгоритм останавливается.

Пример вызова функции для исходного пространства Х и результат

расчета координат центров в матрице ХХ (рис. 9):

r:=CentrClaster(X,α,β,55).

Функция CentrClaster возвращает убывающие по потенциалу коор-

динаты центров. Число координат центров кластеризации (собственно число кластеров) определяется как длина массива r: length(r)=3.

Формирование 1-й и 2-й колонки координат

Особенность алгоритма приводимой функции в том, что начальное множество кандидатов назначается из тех же координатных пар, кото-

рыми описаны объекты в матрице Х. Результат в ХХ − это выборка из Х для центров с максимальным потенциалом. Попробуйте, в качестве са-

мостоятельного задания, реализовать функцию CentrClaster(), опре-

деляя кандидаты независимо от X. Для этого нужно будет решить ша-

ги алгоритма, изложенные в нижеследующем задании практической ра-

боты.

45

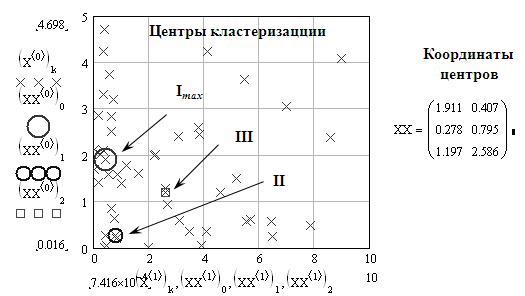
Рис. 9. Результат кластеризации 2-координатного пространства объектов: получены три центра, пронумерованные в порядке убывания рассчитанного потенциала

Рассмотрим пример интерполяции результата решения горным алгорит-

мом на поверхность средствами Mathcad.

46

Используется функция CentrClaster(), но модифицированная таким об-

разом, что возвращает вместе с координатными парами значение по-

тенциала. Координаты − это первая и вторая колонка матрицы ХХ, а

потенциалы ее третья колонка. Начинаем формировать матрицы поверх-

ностей.

и способна представить координатное пространство в виде «горной местности» (рис. 10). Матрица Zc содержит ненулевые значения по-

тенциалов точек, координаты которых были выбраны в качестве цен-

тров кластеров. Итерационный алгоритм остановился, когда уровни оставшихся потенциалов составляли менее 55% от потенциала первой максимальной вершины. В результате были просчитаны три вершины,

потенциал которых не меньше максимального потенциала P(Z1)=10.021 в

указанных процентах.

47

Рис. 10. Решение по горному алгоритму:

А− потенциалы («горный рельеф») первого прохода;

Б− финальные центры кластеров и их потенциальные уровни

Практическое задание: определение начальных условий и отладка одной итерации горного алгоритма.

Содержание задания: пройти путем программирования и отладки одну итерацию горного алгоритма. Итерация сокращена до 3-х шагов.

Подготовка к 1-му шагу заключается в генерации координатного пространства объектов кластеризации Х и координатного пространства назначенных центров-кандидатов Z. Генерацию 2-мерного X, как и все последующие отдельные приемы, смотреть в примере. Важно понимать, что число объектов и начальное число центров-кандидатов (строки матриц Х и Z) могут совпадать, но чаще отличаются. А вот размерность пространств должна совпадать (колонки матриц Х и Z) всегда! Итак, пусть число центров-кандидатов назначено переменной Nz, а число объектов кластеризации переменной N. Сгенерируйте матрицу Z центров-кандидатов с числом строк меньше или равным X.

Н а ч а л о и т е р а ц и и .

На 1-м ш а г е рассчитаем потенциалы вершин назначенных кандидатов и запишем их в 2-ю колонку PZ:

48

Значения координат центров вектора Result это колонки 0 – 1, потенциалы вершин – колонка 2. Произведенная кластеризация по горному алгоритму не является нечеткой, но ее часто используют при синтезе нечетких правил из данных.

Результат практики: это отладка и выполнение заданной итерации. Скопируйте и повторите строки отлаженной итерации шагов 1 – 2 не менее 3-х раз. Убедитесь, что максимальные вершины всех 3-х итераций корректно удаляются, а вектор Result пополняется значениями центров, количество которых должно быть равным числу проделанных итераций.

Контрольные вопросы

1.Какова цель применения горного алгоритма к исходному координатному пространству в задачах интеллектуальных технологий?

2.Какие можно предложить критерии останова алгоритма в отличие от приведенного в примере?

3.Какой параметр алгоритма регулирует (ограничивает) радиус действия вершины как доминирующей при расчете ее потенциала?

50