3.Задача Коши и методы ее решения.

3.1.Постановка задачи

Дифференциальное уравнение первого порядка можно записать в виде

Данное уравнение имеет некоторое семейство решений y(t) и конкретное решение определяется заданными начальными условиями. Начальное значение зависимого переменного может быть задано для любого значения t0 независимого переменного, например t0=0.

Для системы дифференциальных уравнение уравнений первого порядка; например,

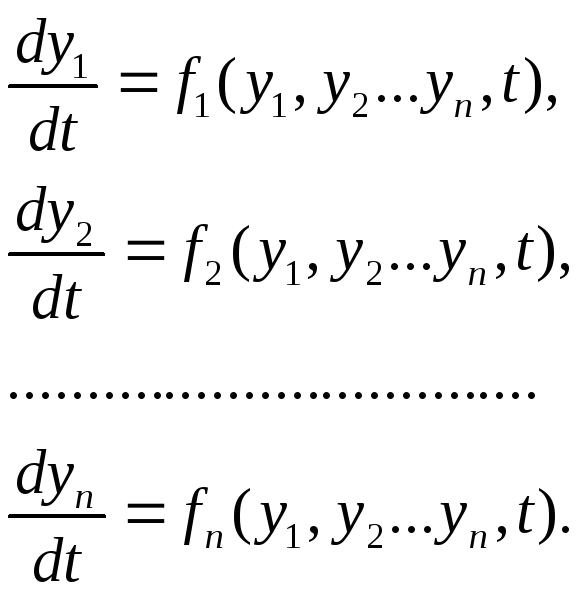
Допустим, что правые части уравнений могут быть определены на всем интервале интегрирования, тогда при известных значения зависимых переменных y₁(t0) , y₂(t0), ...,y_n(t0) для некоторого момента времени система уравнений будет иметь единственное решение.

Любое обыкновенное дифференциальное уравнение порядка n, которое можно записать так, что его левая часть есть производная наивысшего порядка, а в правой части эта производная не встречается, может быть записано и в виде системы изпуравнений первого порядка путем введения (n—1)новых переменных. Например,

можно записать как систему

где , т.е. привести с системе дифференциальных уравнений 1-го порядка.

В векторных обозначениях это выглядит так:

где

.

3.2.Численные методы решения

Метод решения задачи Коши удобно рассматривать на примере одного дифференциального уравнение 1-го порядка

,

,

Лишь очень немногие дифференциальные уравнения могут быть решены точно, и потому обычно необходимо решать задачу численными методами. Любые численных методов являются приближенными и необходима от пользователя следующая дополнительная информации:

Величина допустимой ошибки при решении. Если потребовать бесконечной малой величины ошибки решения, то (за исключением примеров из дисциплины «Высшая математика» и некоторых специально подобранных задач) решение найти невозможно.

Указание допустимых ресурсов ЭВМ (в первую очередь временных), которые пользователь готов выделить на решение задачи.

Решение осуществляется пошаговыми методами (разностными методами или методами дискретного переменного).

Формируется некоторая последовательность значений независимой переменной t₀, t₁, t₂, . t_n, в которых известно точное решение y(t₀), y(t₁), y(t₂),…, y(t_n) . Тогда в точке t_iточное решение y(t_i) заменяется некоторым приближенным значением y_i, которое вычисляется по нескольким предыдущим значениям y_i-1 , y_i-2, y_i-k.

В зависимости от количества используемых в расчете значений переменной методы могут быть одношаговыми, требуется значение y_i-1 , и k-шаговыми, требуются значения y_i-1, y_i-2, y_i-k.

Используют как методы с заданной величиной шага изменения независимой переменной, так и с переменной длиной шага h_i=t_i-t_i-1.

Примером одношагового метода является метод Эйлера. В методе Эйлера значение y_i+1вычисляется при помощи линейной экстраполяции из предыдущей точки y_i. Рассмотрим уравнение

,

при начальном условии

.

Тогда значение в точке t₁= t₀+h0 можно найти, выполнив разложение функции y(t₁)=y(t₀+h₀) ряда Тейлора (два первых члена ряда):

Значение в точке t2=t1+h1 рассчитывается аналогично:

и в общем случае используется соотношение

Для успешного применения метода Эйлера необходимо в уравнения подставить значение правой части в задаче Коши.