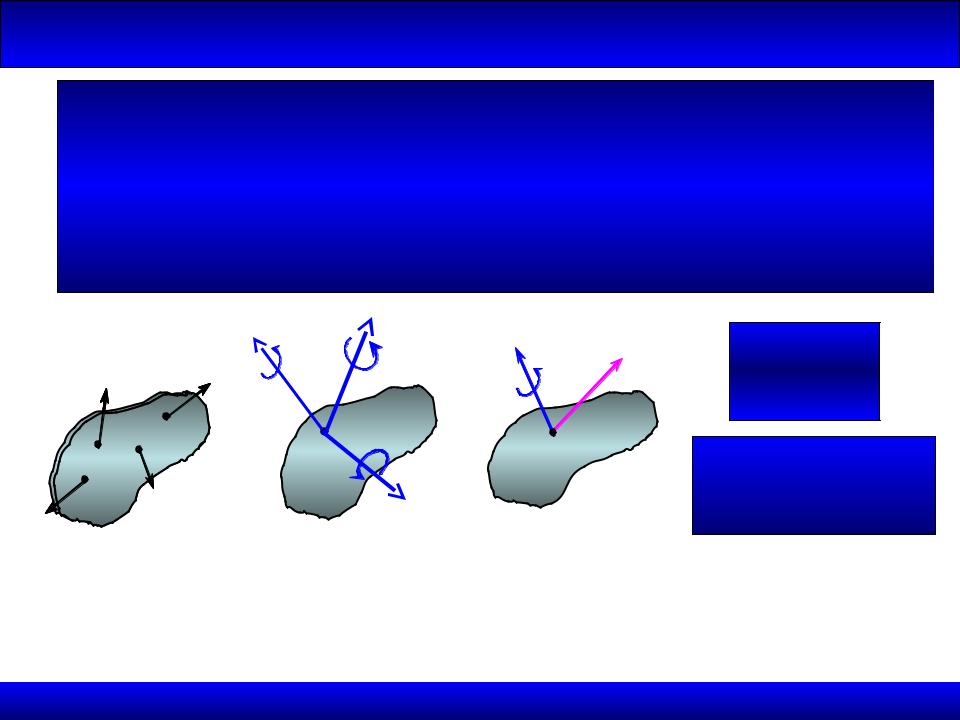
Теорема1.6.4.ТеоремаравнодействующейПуансо (1804 г.)двух сил

Произвольную систему сил можно заменить одной силы, приложенной в произвольно выбранной точке (центре приведения) и равной главному вектору системы сил, и парой сил с моментом, равным главному моменту системы относительно этой точки

•Пользуясь леммой о параллельном переноса силы, перенесем их все параллельно в точку А

Теорема доказана

1.6.5. Уравнения равновесия Равнодействующая СПС

Пусть дана произвольная система сил {F1, F2 ,..., Fn}. Тело под действием этой системы сил находится в равновесии, если она эквивалента нулю {F1, F2 ,..., Fn} ~ 0

Но

{F1, F2 ,..., Fn} ~ {R*, MO* )} ~ 0

В координатной форме эти уравнения равновесия имеют вид

1.6.6. Уравнения равновесия ПСС Равнодействующая СПС

Пусть все силы находятся в плоскости Oxy. В этом случае проекция главного вектора на ось Oz равна нулю, а главный момент направлен параллельно этой оси. Т.о., имеем три уравнения равновесия.

Основная форма уравнений равновесия ПСС

Вторая форма уравнений равновесия ПСС (АВ Ox)

Третья форма уравнений равновесия ПСС (точки А, В, С не

должны лежать на одной прямой)

1.6.7. Статические инварианты

Инварианты – величины, неизменные при некотором преобразовании. Статические инварианты – величины, не зависящие от выбора центра приведения.

• I статический инвариант – главный вектор системы сил

i1

•II статический инвариант – скалярное произведение главного вектора и главного момента системы

M A* R* inv

1.6.8. Частные случаи приведения

•R* 0, M А* 0 , но M *A R* – в этом случае система сил приводится к равнодействующей. Действительно, M A* R* 0

M A*

F'

F R А R*

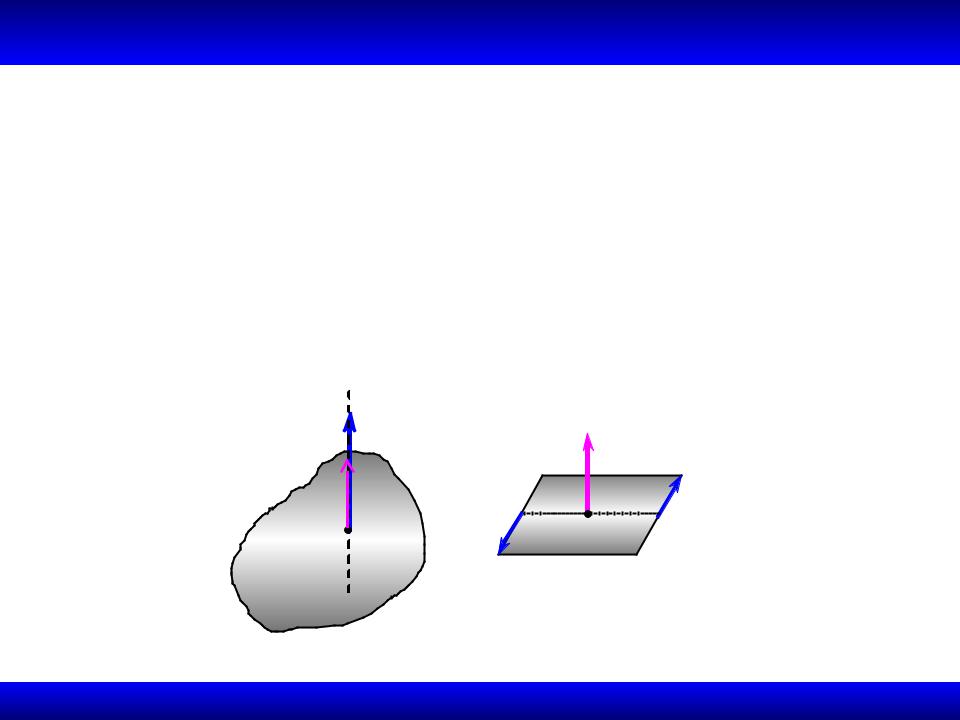
1.6.8. Частные случаи приведения

• R* 0, M А* 0 , но M A* || R* – в этом случае система сил приводится к приводится к силе R* и паре сил (P1, P2 ),

лежащей в плоскости, перпендикулярной к R* . Такая совокупность силы и пары сил называется динамой, а

прямая, вдоль которой направлен главный вектор, – осью динамы.

I. Статика

I.7. Трение

67

1.7. Трение

•Законы трения покоя

•Законы трения скольжения

•Реакции связей при учете трения

•Угол трения

•Конус трения, заклинивание

•Измерение коэффициента трения

•Трение качения

•Равновесие при наличии трения

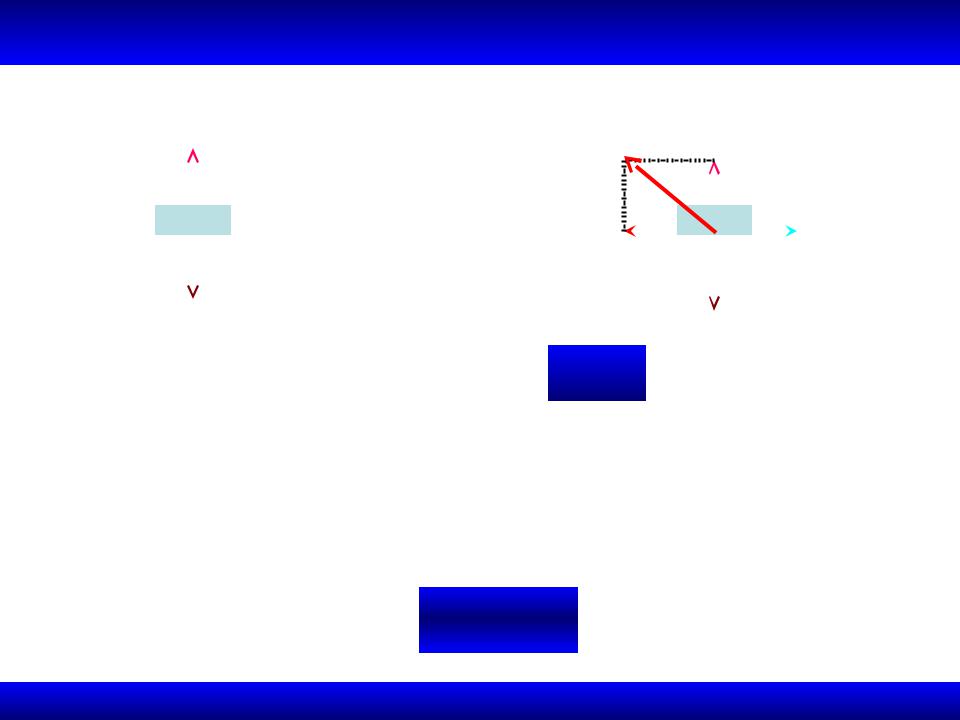
1.7.1. Сила трения покоя

• Возникает сила, препятствующая движению под действием силы

• Движение возникает лишь когда F Ff*

•Сила трения покоя может принимать любые значения от нуля до некоторого максимального, называемого предельной силой трения покоя. Направлена она в сторону, противоположную той, куда действующие активные силы стремятся сдвинуть тело

• Закон Кулона-Амонтона Ff* fs N Как определить fs ?