1.5.4. Момент пары как вектор
z |
|
А |
F1 |
|
B |
O |
y |
|
Момент пары сил (F, F1) равен
MM A (F2 ) M B (F1) AB F2
•Введем систему координат Оxyz
M AB F2 (OB OA) F2OB F2 OA
F2 OB F2 OA
F1
x
M MO (F1) MO (F2 )
Сумма моментов сил пары относительно любой точки О равна моменту пары этих сил. Поскольку момент пары сил перпенди- кулярен плоскости пары, а его модуль равен M AB F1 sin(AB, F1), то момент пары не зависит от точек приложения сил пары.
Он определяется лишь плечом пары.
1ПАРА2.15. ОПРЕДЕЛЕНИЕТЕОРИЯСИЛ ПАР СИЛССС |
52 |
1.5.5. Теорема об эквивалентности пар сил
Доказательство
Все пары сил, имеющие один и тот же момент, |
|||||||
эквивалентны. |
|
|
|
||||
Доказательство |
|
Дана пара сил (F, F ) с моментом m = Fh |
|||||
|
|
|
|
|
|
• Разложим каждую из них по двум |
|
|
|
|
|
Q |
|
|
направлениям на силы { f ,Q},{ f ,Q } |
|
|
|
|
|
(F, F ) ~ ( f ,Q, f ,Q ) но ( f , f ) ~ 0 |
||
|
|
|
|
C F |
|
||
|
A |
d |
|
|
(F, F ) ~ (Q,Q ) |
||
|
|
|
|
|
|||
|
|
|
B |
|
|
• Момент пары (Q,Q )равен m Qd |
|
f |
|
|
h |
|
f |
||
F |
|
|
|
||||
|
|
|
|
|
Так как ABC ~ FQf то d hF Q |
||
|
|
Q |
|
|
|
|
m Qd (Qh)F / Q Fh m |
Теорема доказана для пар, лежащих в одной плоскости
1ТЕОРЕМА2.15. ОПРЕДЕЛЕНИЕТЕОРИЯОБПАРЭКВИВАЛЕНТНОСТИСИЛССС |
ПАР СИЛ |
52 |
|
|
|
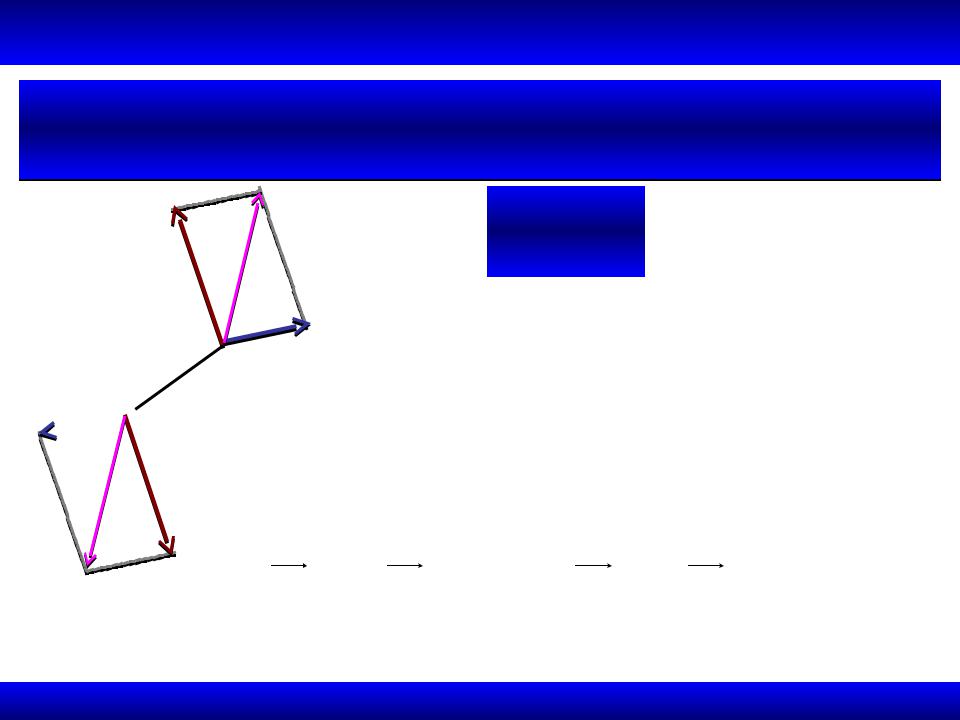
1.5.6. Теорема об сложении пар сил
Доказательство
Действие на тело системы пар с моментами M1, M2 ,...,M N
Эквивалентно действию одной пары с моментом
Q1
A
F1 
B
R1 Q1
|
|
N |
|
|
|
|
|
|
M Mk |
|
|
|
|||
R1 |
|
k 1 |
|
|
|
|
|
• Докажем сначала теорему для двух пар сил |
|||||||
|
|||||||
F1 |
• Из теоремы об эквивалентности пар следует, что |
||||||
|
для доказательства достаточно рассмотреть две |
||||||
|
пары, точки приложения сил которых A и B |
||||||
|
совпадают |
|
|
|
|
|
|
|
• Рассмотри две пары сил (F , F ) и (Q ,Q ) |
||||||
|
|
|
1 |
1 |
1 |
1 |
|
• Действие рассматриваемых двух пар эквивалентно |
|||||||
|
действию одной пары (R1, R1 ) |
с моментом |
|
||||
M AB R1 AB (F1 Q1) AB F1 AB Q1 M1 M2
Для N пар можно доказательство получается по индукции.
ТЕОРЕМА СЛОЖЕНИИ ПАР СИЛ |
53 |
12.15. ОПРЕДЕЛЕНИЕТЕОРИЯ ПАР СИЛССС |
1.5.7. Условия равновесия тела под действием системы пар
• |
Действие на тело произвольной системы пар сил с |
|||||
|
моментами M1, M2 ,...,M N |
эквивалентно действию |
||||
|
одной пары с моментом |
|
N |
|
||
|
M M k |
|
||||
|
|
|
|
|
k 1 |
|
• |
Для того чтобы тело под действием системы пар тело |
|||||
|
находилось в равновесии, необходимо и достаточно, |
|||||
|
чтобы |
|
N |
|
|
|
|
|
|
|
|||
|
|
M M k 0 |
|
|||
|
|
|
k 1 |
|
|
|
Уравнения равновесия |
|
|
N |
|||
|
N |
|
|
N |
|
|
|
M x M kx 0, |
|
M y M ky 0, |
M z M kz 0 |
||
|
k 1 |
|
|
k 1 |
N |
k 1 |
|
|
|
|
|
|
|
Для плоской системы сил |
|
mk 0 |
||||
1.5. ТЕОРИЯ ПАР СИЛ |
|
|
|
k 1 |
54 |
|
|
|
|
|
|||
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
|
|
|
|
||
1.5.8. Жесткая заделка
•Жесткая заделка – это вид связи, полностью запрещающей движение тела
•Пример – балка, один конец которой защемлен
•Реакция жёсткой заделки представляет собой совокупность силы и пары сил, которые образуют плоскую или пространственную систему сил в зависимости от того, какими являются активные силы.
Графическое представление |
Реакция жесткой заделки |
y
YA
А
mA |
x |
X A |
1.5. ТЕОРИЯ ПАР СИЛ |
55 |
|
2.25. УСЛОВИЯРЕШЕН |
РАВНОВЕСИЯЗАДАЧ СТАТИКИ |
|
I. Статика
I.6. Основная теорема статики
56
1.6. Основная теорема статики
•Теорема о параллельном переносе силы
•Главный вектор и главный момент системы
•Основная теорема статики (теорема Пуансо)
•Условия равновесия произвольной системы сил
•Уравнения равновесия
•Три формы уравнений равновесия ПСС
•Приведение пространственной системы сил к простейшему виду
•Статические инварианты
11.24.6. ОСВЯЗИ. СТАТИКАНОВНЫЕИ РЕ ПОНЯТИЯКЦИИ СВЯЗЕЙИ МОДЕЛИ |
57 |
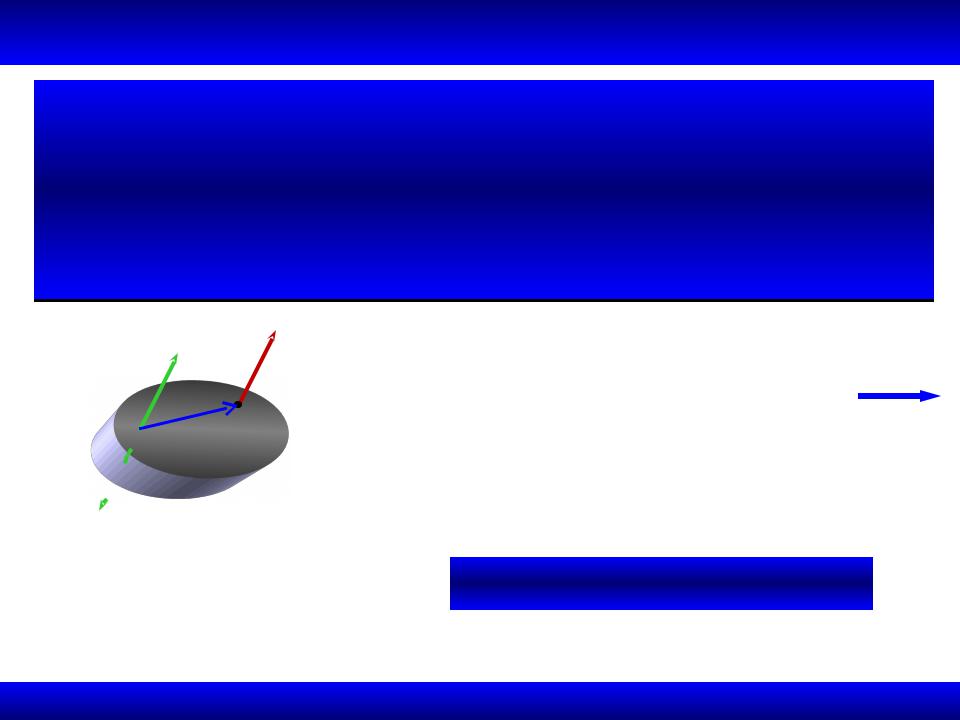
1.6.1. Лемма о параллельном переносе силы
Действие на твердое тело силы F , приложенной в точке A, эквивалентно действию силы F' , равной исходной по модулю, параллельной ей и приложенной в точке В, и
паре сил с моментом равным моменту данной силы относительно точки В
F'
В
F
'
Доказательство
F • |
Добавим к силе F уравновешенную |
|
A |
систему сил{F', F'} ~ 0 в точке В |
|
F ~ {F, F', F'} |
||
|
||
• |
Но силы F, F' образуют пару сил с |
|
|
моментом |
M (F, F') BA F M B (F)
Теорема доказана
12.61. ОСНОВНАЯПРЕДЕЛЕНИЕТЕОРЕМАССС СТАТИКИ |
58 |
1.6.2. Главный вектор
Главным вектором данной системы сил называется вектор R*, равный сумме всех сил системы
n
R* Fi
i 1
Замечание
•Главный вектор определен для любой системы, а равнодей- ствующая в ряде случаев просто не существует
•Главный вектор системы сил не зависит от центра приведения
12.16. ОСНОВНАЯПРЕДЕЛЕНИЕТЕОРЕМАССС СТАТИКИ |
59 |
1.6.3. Главный момент
Главным моментом данной системы сил относительно точки А называется вектор M A* , равный сумме моментов всех сил системы относительно той же точки
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M * |
|
|
M |
Ai |
M |
A |
(F ) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
Замечание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
Главный момент меняется при смене центра приведения |
|
|
||||||||||||||||||||
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, |
Ai |
r |
F |
|
|
M Bi |
rBK Fi |
|
|
|
|
|
|||||||||||
|
|
AK |
, аi |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Fi |
|
|
|
|
** |
|
|
n |
|
|
|
n |
|
|
|
|
|||
|
|
rAK |
|
|
|
|
MAA M A (Fi ) rAK Fi |
|
|
||||||||||||||
|
|
|
К |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
i 1 |
|
|
|
|
|
||
А |
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
r |
|
rВK |
|
(rAB |
rBK ) Fi |
rAB Fi |
rBK Fi |
||||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|
|||
|
|
АВ |
|
|
|
|
|
|
|
|
|
R* M B* |
|
|
|
|
|
|
|
||||
|
|
|
B |
|
|
|
|
rAB |
|
|
|
|
|
|
|
||||||||
12.16. ОСНОВНАЯПРЕДЕЛЕНИЕТЕОРЕМАССС СТАТИКИ |
60 |