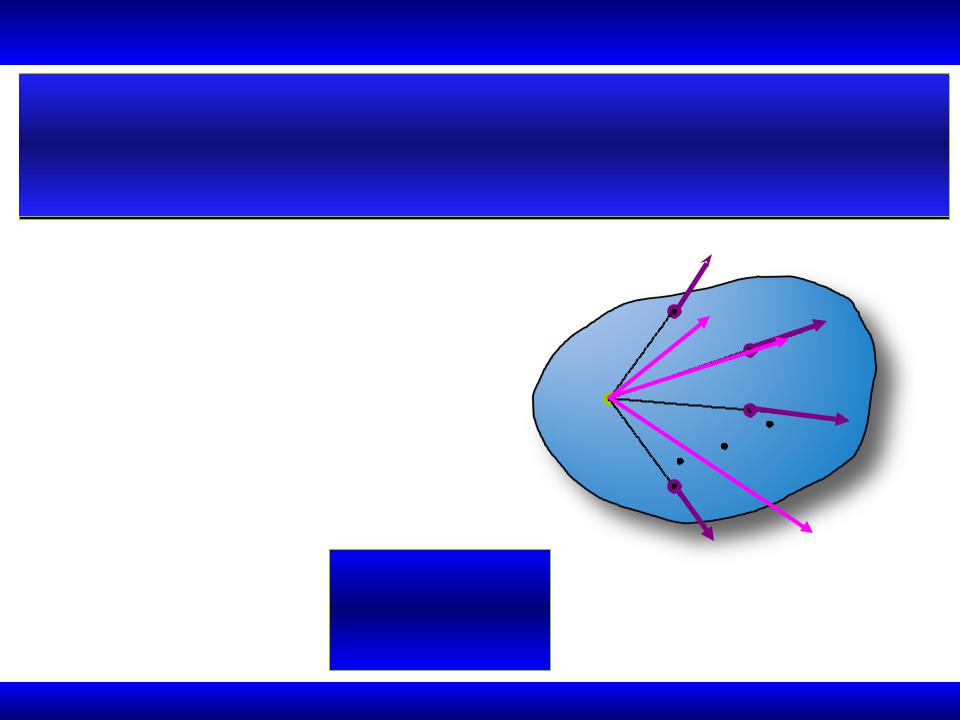
1.2.2. Теорема о равнодействующей CCC
Система сходящихся сил имеет равнодействующую, равную геометрической сумме этих сил и проходящую через точку пересечения их линий действияF1
Доказательство |
|
|
|
F1 R12 |
|
||
• |
Перенесем силы в точку |
|
|
F2 |
|||
|
пересечения линий действия |
|
|
|
|||
• |
Складывая затем силы попарно |
|
|
R123 |
|||
|
по правилу параллелограмма |
|
С |
|
F3 |
||
|
R12 F1 |
F2 , |
|
|
|
FN |
|
|
R123 R12 F3 |
F1 F2 |
F3, |
|
|
|
|
|
|
|
|
||||
|
…….. |
|
N |
|
|
R |
|
|
|
R Fi |
Теорема доказана |
||||
|
|
|
|
i 1 |
|
|
|
1.2. СИСТЕМА СХОДЯЩИХСЯ СИЛ |
|
|
|
21 |
|||
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
|
|
|
|
|||
1.2.2. Аналитический способ определения равнодействующей ССС
n |
n |
|
|
|
R Fk i Fkx jFky kFkz |
||||
k 1 |
k 1 |
|
|
|
n |
|
|
|
|
i Rkx |
jRky kRkz |
|
||
k 1
Где Rx, Ry, Rz – проекции равнодействующей на оси x, y, z
n |
n |
n |
Rх Fkx , |
Ry Fky , Rz Fkz |
|
k 1 |
k 1 |
k 1 |
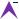
R kRz 
jRy
i Rx
Rxy
R 
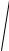Rx2 Ry2 Rz2
|
Rx |
|
|
|
Ry |
|
|
|
Rz |
|||||||
cos(R,x) |
|
|
|
, |
cos(R,y) |
|
|
|
, |
cos(R,z) |
|
|
|
|
|
|
|
|
|
|
R |
|
|||||||||||
|
R |
|
|
|
|
|
R |
|
|
|
||||||
|
|
|
|
|
|
|||||||||||
1.2. ССС |
|
|
|
|
|
|
|
|
|
|
22 |
|||||
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
|
|
|
|
|
|
|
|
||||||||
1.2.3.Геометрический способ определения равнодействующей ССС
•Равнодействующая может быть найдена геометрически
•Она является замыкающей стороной силового многоугольника, построенного на данных силах
|
N |
|
|
|
R Fi |
|
|
||
|
i 1 |
F1 |
F |
R |
|
|
|||
|
|
|
2 |
|
|
|
F |
|
F3 |
|
|
N |
|
F4 |
|
|
|
|
|
1.2. ССС |
23 |
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
1.2.4. Условия равновесия тела под действием ССС
Действие на тело произвольной ССС эквивалентно |
||||
действию одной силы, равнодействующей |
||||
|
|
|
|
N |
{F1 |
, F2 |
, , F1} ~ R Fi |
||
i 1
Но если тело находится в равновесии под действием одной силы, то эта сила равна нулю
N |
|
R Fi |
0 |
i 1
Геометрически это условие означает замкнутость силового многоугольника сил {F1, F2 , , F1}
1.2. ССС |
24 |
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
1.2.5. Уравнения равновесия CCC
Тело под действием ССС находится в равновесии, если
R i Rx jRy kRz 0
Это векторное уравнение содержит сумму трех взаимно перпендикулярных векторов. Поэтому оно удовлетворяется только, если нулю равен каждый, из слагаемых
n |
n |
n |
Rx Fix 0, |
Ry Fiy 0, |
Rz Fiz 0 |
i 1 |
i 1 |
i 1 |
Если на тело действует плоская ССС, скажем, в плоскости xy, то данная система уравнений сводится к следующей
n |
n |
Rx Fix 0, |
Ry Fiy 0 |
i 1 |
i 1 |
1.2. ССС |
25 |
2.32. УСЛОВИЯРАВНЕНИЯРАВНОВЕСИЯ |
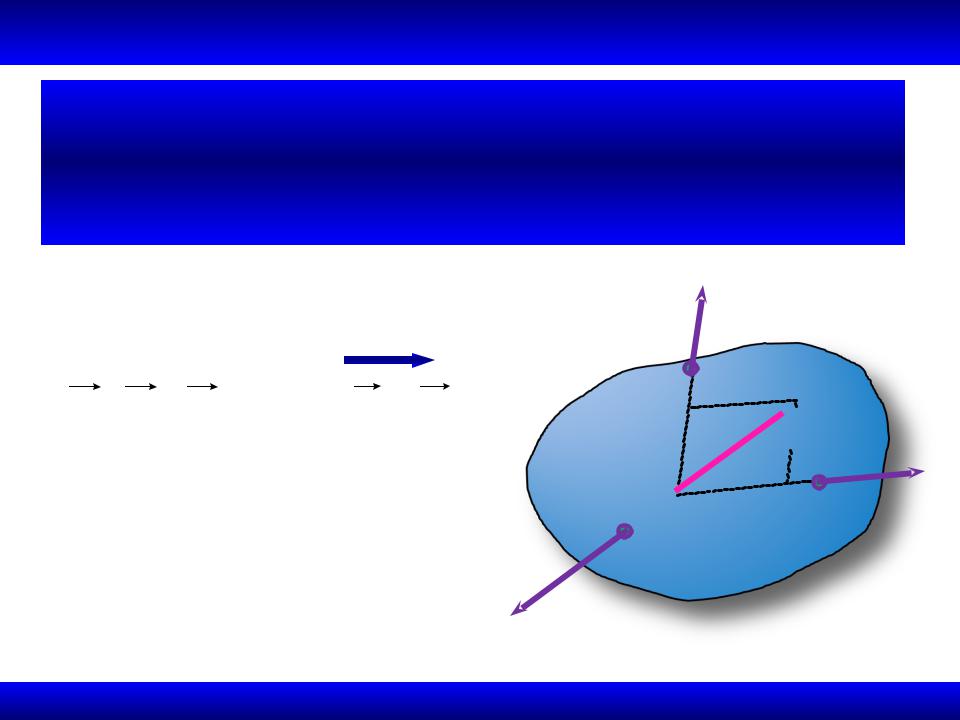
F1 1.2.6. Теорема о трех силах
Если твердое тело находится в равновесии под действием трех сил, причем линии действия двух из них пересекаются, то эти силы образуют ССС
Доказательство
Пусть линии действия двух первых |
F1 |
сил пересекаются |
|
( F1,F 2 ,F 3 ) ~ ( R12 ,F 3 )
Но согласно А1 эти силы должны быть равны по величине и противоположно направлены 
R12
С F2
F3
Линия действия силы проходит через С. Теорема доказана
1.2. ССС |
26 |
2.24. УСЛОВИЯТЕОРЕМА РАВНОВЕСИЯТРЕХ СИЛАХ |
1.2.7. Алгоритм решения задач статики
1.Установить, исследование равновесия какого тела (точки, системы тел) следует рассмотреть
2.Освободить тело от связей и изобразить действующие на него активные силы и силы реакций отброшенных связей
3.Установить, какая система сил действует на тело, и сформулировать условия равновесия этой системы
4.Составить уравнения равновесия
5.Решить уравнения равновесия и определить искомые неизвестные
Замечание
Если число неизвестных не превышает числа уравнений равновесия, то система называется статически определенной, в противном случае – статически неопределенной
1.2. ССС |
27 |
2.25. УСЛОВИЯРЕШЕН РАВНОВЕСИЯЗАДАЧ СТАТИКИ |
I. Статика
I.3. Момент силы
28
1.3. Момент силы
•Момент силы относительно точки
•Момент силы относительно оси
•Теорема Вариньона для ССС
•Теорема о связи момента силы относительно точки и относительно оси
•Алгебраическое понятие момента силы для ПСС
•Плечо силы
I1..24СТАТИКА. ОСНОВНЫЕСВЯЗИ И РЕАКЦИИПОНЯТИЯСВЯЗЕЙИ МОДЕЛИ |
29 |
1.3.1. Момент силы относительно точки
|
|
|
|
Моментом силы F относительно точки |
||
|
|
|
|
О называется вектор |
M, равный(F) |
|
|
|
|
F |
|
|
o |
|
h |
|
векторному произведению радиус- |
|||
|
|
|
вектора |
r |
|
|
Mo |
|
|
точки приложения силы и |
|||
|
r |
A |
силы: |
|
|
|
O |
|
|
Mo (F) r F |
|||
|
|
|
|
|
|
|
Момент силы направлен перпендикулярно плоскости векторов r и F и в ту сторону, откуда вращение тела
происходит против часовой стрелки
|
|| F | sin |
h | r | sin |
| Mo (F) | Fh |
| Mo (F) | | r |
Плечо силы h – это кратчайшее расстояние от точки относи-
тельно которой вычисляется момент до линии ее действия
1.3. МОМЕНТ СИЛЫ |
22 |
2.2. УСЛОВИЯ РАВНОВЕСИЯ |