1.3.1. Момент силы относительно точки
|
|
|
|
|
|
|
|
|
|
|
|
Mo (F) r F |
|
|
|
|
i j |
k |
|
|
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
||
MO (F) |
|
x y |
z |
|
( yFz zFy )i (zFx xFz ) j (xFy yFx )k |
|
|
|
|
Fx Fy Fz |
|
|
|
|
|
|
|
|
||
где x, y, z – координаты точки приложения силы, а Fx , Fy , Fz– проекции силы на оси координат
Mo (F) i Mox jMoy kMoz 
MOx (F) yFz zFy , |
MOy zFx xFz , |
MOz (F) xFy yFx |
|
|
|
1.4. МОМЕНТ СИЛЫ |
|
31 |
1.3. МОМЕНТ СИЛЫ |
|
|
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
|
|
|
|
18 |
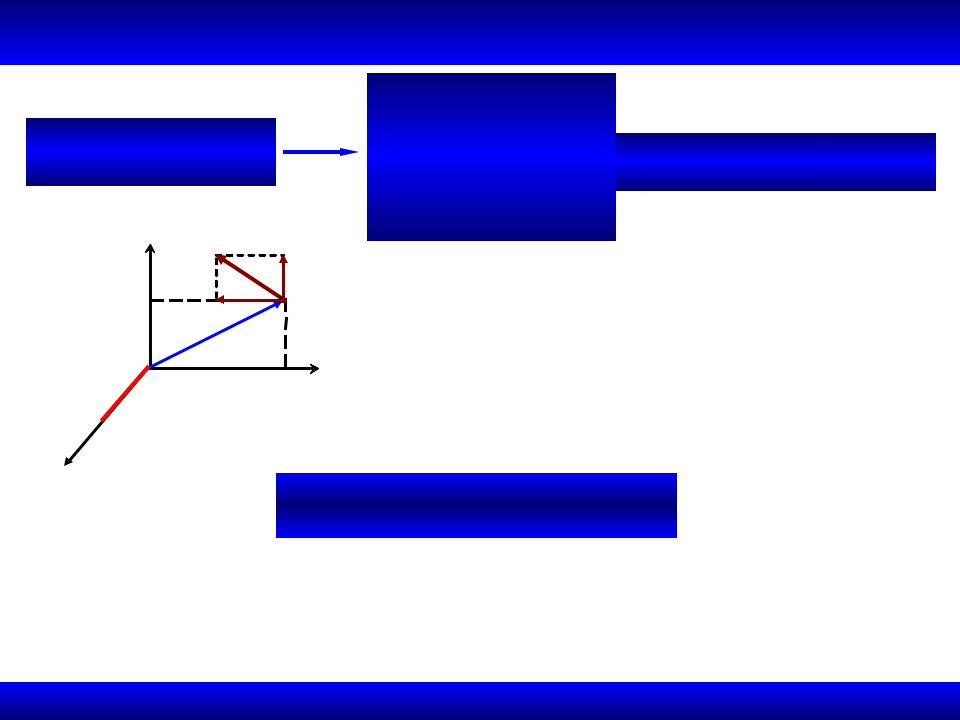
1.3.2. Момент силы на плоскости
|
|
|
|
Mo (F) r F |
|
||
Y |
F |
Fy |
|
|
|||
y |
Fx r |
A |
|
X |
|||
O |
x |
||
|
|||
|
|
||
MO (F)
Z
|
|
|
i j k |
|
|
|
|
|
|
||
MO (F) |
x y 0 |
(xF yF )k |
Fhk |
||
|
|
|
Fx Fy 0 |
y x |
|
|
|
|
|
|
|
|
|
|
|
MO (F) ||k |
|
|
|
F OXY |
|||
• Вектор момента силы имеет одну
составляющую и направлен перпен- дикулярно плоскости, в которой лежит сила и центр
mO (F) MO (F) F h
•Алгебраический момент силы mO (F) имеет знак плюс, если под действием силы тело поворачивается против часовой стрелки, и минус – в противном случае
1.3. МОМЕНТ СИЛЫ |
32 |
12.24. УСЛОВИЯЕНТ СИЛЫРАВНОВЕСИЯ |
|
|
20 |
1.3.3. Теорема Вариньона
Момент равнодействующей системы сходящихся сил относительно произвольной точки O равен векторной сумме моментов слагаемых сил относительно той же точки
Доказательство
Векторное произведение удовлетворяет закону дистрибутивности
|
F2 |
|
|
|
r (F1 |
Fn ) r F1 |
r F2 |
r Fn |
R F1 F2 Fn
M (F )
MO (R) rО (F1 F2 Fn ) O k
Теорема доказана
1.3. МОМЕНТ СИЛЫ |
33 |
12.24. УСЛОВИЯЕНТ СИЛЫРАВНОВЕСИЯ |
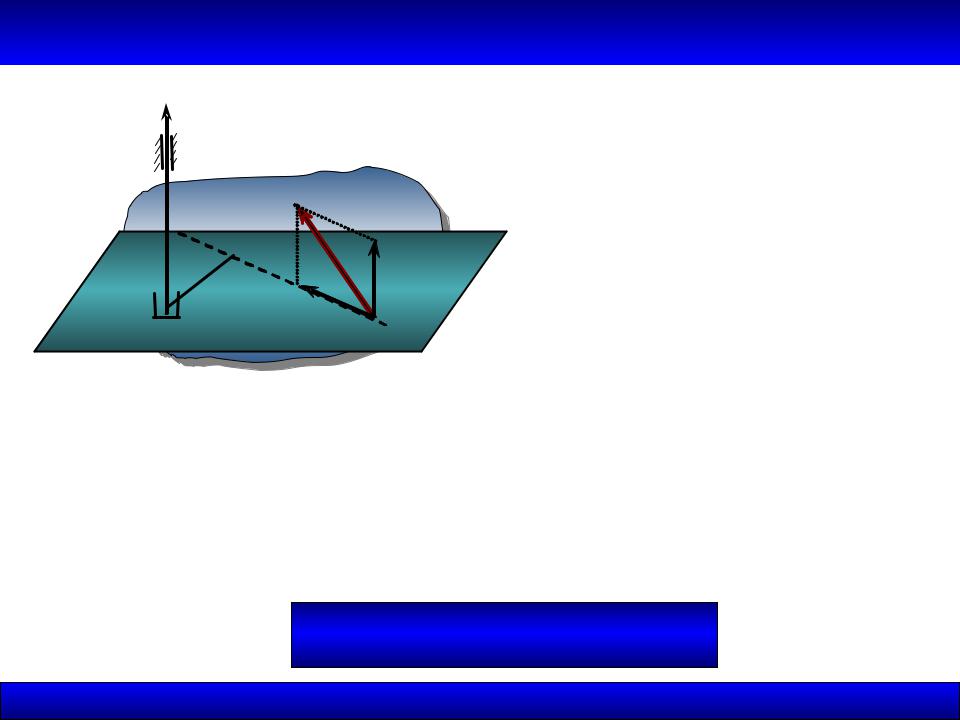
F 1.3.4. Момент силы относительно оси
z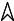 
F
|
O |
h |
F |
Fz |
|
(xy) |
A |
||||
|
|
xy |
|||
|
|
|
•Тело под действием данной силы будет вращаться относительно оси Oz
•Это вращение характеризу- ется скалярной величиной, называемой моментом силы относительно оси Oz
•За вращательное движение отвечает сила
Моментом силы F относительно оси OZ называется скалярная
величина, равная алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси относительно точки пересечения данной оси с этой плоскостью
M z (F) M z (Fxy ) Fxy h
1.3. МОМЕНТ СИЛЫ |
34 |
2.2. УСЛОВИЯ РАВНОВЕСИЯ |
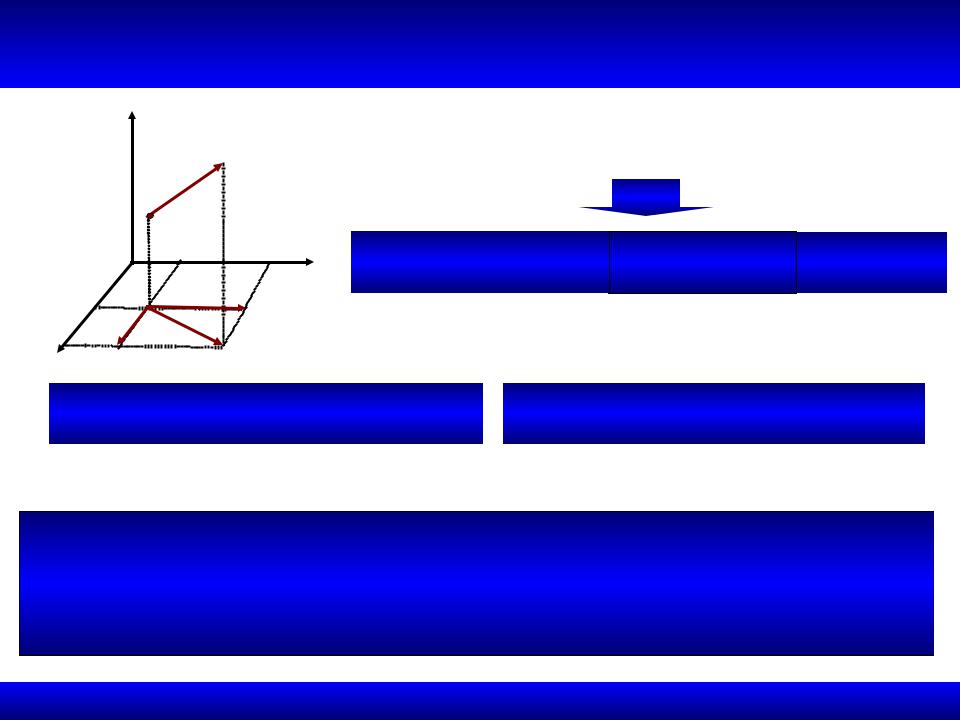
1.3.5. Теорема о связи момент силы относительно точки и оси
Z
F
|
|
A |
y |
Y |
|
O |
|
||
|
|
|
|
|
|
x |
|
|
Fy |
X |
|
|
|
|
Fx |
|
|
Fxy |
|
|
|
|
Чтобы найти момент силы F относительно оси Oz, воспользуемся теоремой Вариньона
M z (F) M z (Fxy ) xFy yFy MOz (F)
Аналогично
M x (F) MOx (F) yFz zFy , |
M y (F) MOy (F) zFx xFz |
Теорема
Моменты сил относительно осей в системе координат ОXYZ равны проекциям момента силы относительно начала координат О
1.3. МОМЕНТ СИЛЫ |
35 |
12.24. УСЛОВИЯЕНТ СИЛЫРАВНОВЕСИЯ |
|
|
24 |
I. Статика
I.4. Система параллельных сил (СПС)
36
1.4.Система параллельных сил
•Теорема о сложении двух параллельных сил, направленных в одну сторону
•Разложение данной системы на две ей параллельные
•Центр СПС
•Центр тяжести
•Методы определения центров тяжести
•Распределенные силы
I1..24СТАТИКА. ОСНОВНЫЕСВЯЗИ И РЕАКЦИИПОНЯТИЯСВЯЗЕЙИ МОДЕЛИ |
37 |
1.4.1. Теорема о равнодействующей двух сил
Система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, равную по модулю сумме их модулей, параллельна им и направлена в ту же сторону.
Линия действия равнодействующей делит отрезок между точками приложения данных сил обратно пропорционально их величине
12.14. ОСПС,РЕДЕЛЕНИЕНАПРАВЛЕННЫЕССС В ОДНУ СТОРОНУ |
38 |
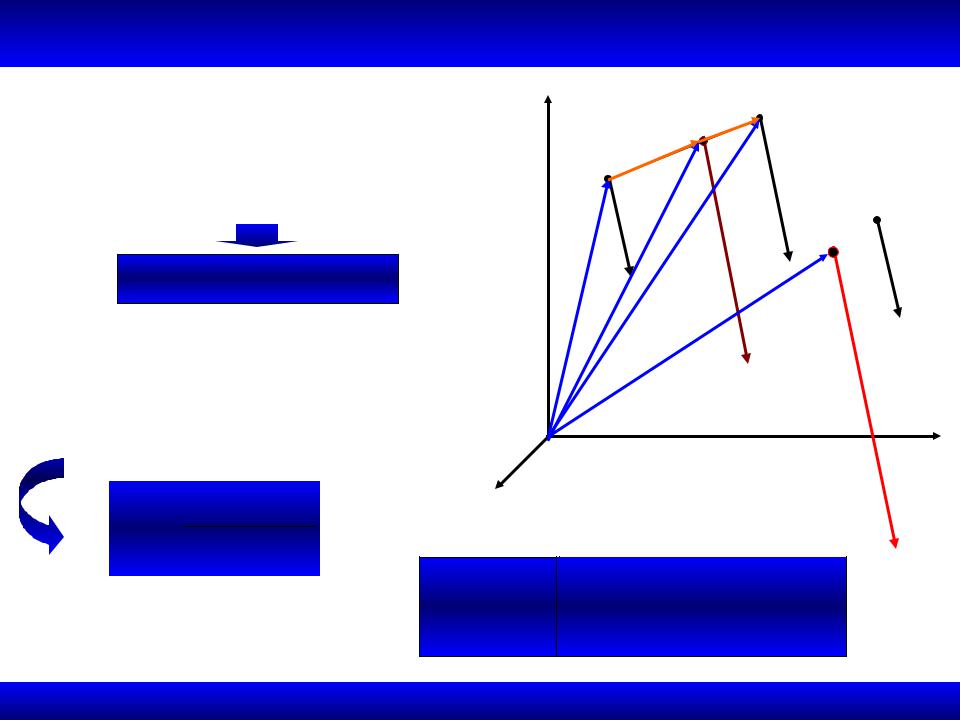
1.4.2. Центр параллельных сил |
|
|
|
|
|
||||||||
Равнодействующая СПС |
|
|
|
|
|
|
|||||||
Дана СПС {P1, P2 ,..., Pn} |
|
|
|
z |
|
C |
|
A2 |
|
|
|||
• Равнодействующая сил P1, P2 |
|
|
A |
1 |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
R12 P1 P2 |
и A1C1 / P2 C1 A2 / P1 |
|
|
1 |
rC1 |
|
|
|
|
||||
|
r1 |
P |
|
P ... |
An |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
C |
||
|
A1C1 / P2 C1A2 / P1 |
|
|
|
|
1 |
r2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
• |
|
|
|
|
|
|
|
|
|
||||
Введем систему координат |
|
|
|
|
|
|
|
|
|
Pn |
|||
• |
Тогда для радиус-векторов точек |
|
|
|
rС |
R12 |
R |
||||||
|
приложения сил имеем |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
(rC1 r1 ) / P2 |
(r2 rC1 ) / P1 |
|
x |
|
|
|
|
|
|
|
y |
|
|
|
Pr |
P r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
r |
1 1 |
2 2 |
|
|
|
|
|
|
|
|
|
|
|
C |
P1 |
P2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
n |
|
|
||
• Далее по индукции можно |
, |
|
|
|
|||||||||
P Pi |
|
rC R 1 |
Piri |
|
|||||||||
|
доказать, что |
|
|
i 1 |
|
|
|
|
|
i 1 |
|
|
|
132.143..ОСПСЦЕНТРРЕДЕЛЕНИЕСИСТЕМЫСССПАРАЛЛЕЛЬНЫХ СИЛ |
|
|
|
|
|
|
|
12 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
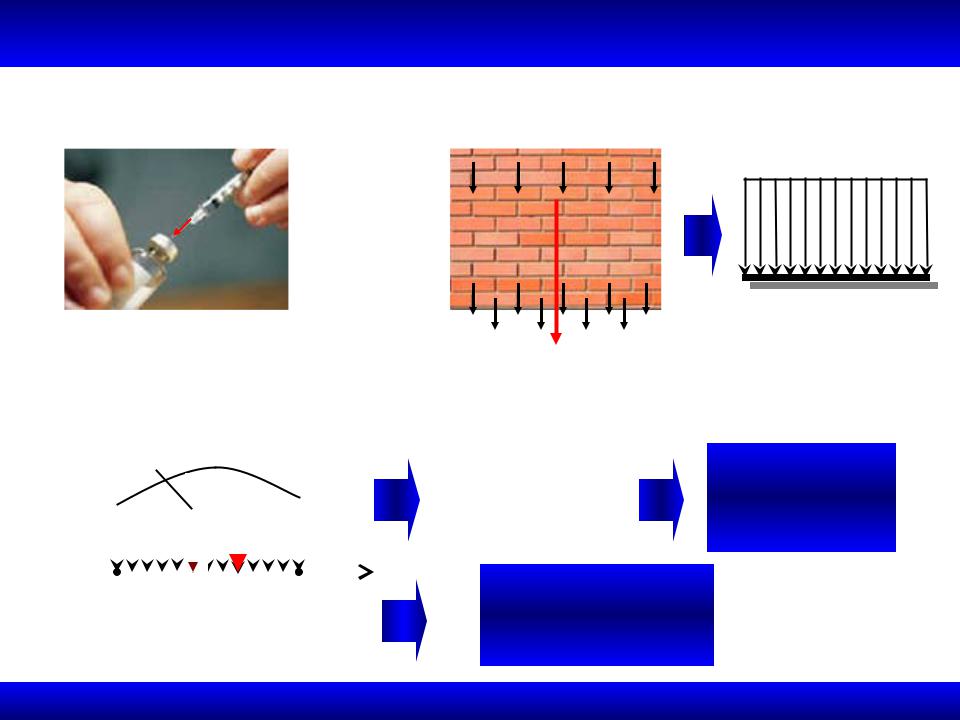
1.4.3. Распределенные силы Распределенные силы
Сосредоточенная сила |
Распределенная нагрузка |
…
Сила, действующая на единицу длины линии, называется интенсивностью нагрузки q
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
B |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
q(xi ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q q(xi ) xi |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q x |
|
|
|
|
Q q(x)dx |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 B |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x xQ B |
|
|
|
|
||||||||||||||||
O A |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xQ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
||||||||
A
132.143..ОСПСЦЕНТРРЕДЕЛЕНИЕСИСТЕМЫСССПАРАЛЛЕЛЬНЫХ СИЛ |
40 |
|
13 |