
Основы высшей математики для инженеров 2009
.pdf
6.4. Потенциальное и соленоидальное поля. Уравнение Лапласа |
301 |
П р и м е р. Найдем div(rot F ).
Пользуясь оператором Гамильтона, получим
div(rot F ) ( F ) ( ) F 0.
Таким образом, поле вихрей всегда соленоидально (свободно от ис# точников).
6.4.3. Уравнение Лапласа
Пусть задано потенциальное поле F . Как было показано выше, та# кое поле всегда является полем градиента некоторой функции
F gradU U i U j U k .
x y z
Потребуем, чтобы это поле было также и соленоидальным. Тогда
div gradU |
|
|
U |
|
U |
|
|
U |
|
2U |
|
2U |
|
2U |
0. |
(1) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x2 |
y2 |
z2 |
||||||||||||||||||
|
x |
x |
|
y y |
|
|
|
z |
z |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
следующим образом: |
|
|
|
|
|
|
||||||||||||||
Оператор , определяемыйM62 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
U |
2U |
|
|
|
2U |
|
2U |
, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
z |
|
|
|
|
|
|
|
|
|||
называется оператором Лапласа. Используя этот оператор, уравне# ние (1) можем переписать в виде
U 0. |
(2) |
Уравнение (2) — уравнение Лапласа. Функция U, являющаяся ре# шением уравнения Лапласа, называется гармонической функцией.

ГЛАВА 7
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
7.1. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка
Задачи, приводящие к дифференциальным уравнениям. Дифференци альные уравнения первого порядка. Задача Коши. Теорема Коши. Общее решение. Особые решения.
Теория дифференциальных уравнений является частью математи ческого анализа. Она дает мощный аппарат для исследования много образных процессов, протекающих в природе и в технике. Дифферен циальные уравнения моделируют процессы в различных объектах и устройствах, поведение которых определяется такими характеристика ми переменных состояния,M62как скорость, ускорение, температура, дав ление, напряжение, радиация и т. д. Поэтому с решением дифферен циальных уравнений неизбежно связаны практически все исследова ния по проектированию и разработке новой техники, технологических процессов, стратегических военных операций, экономических проек тов, химических процессов и многие другие.
7.1.1. Задачи, приводящие к дифференциальным уравнениям
При решении многих задач механики, физики, техники зачастую сразу не удается установить связь между искомой и заданной перемен ными величинами. Однако бывает возможно установить зависимость между заданной переменной, искомой функцией и ее производными. При этом приходим к дифференциальным уравнениям.
П р и м е р. Тело брошено на Землю вертикально вниз с начальной скоростью v0. Определить скорость тела в момент времени t t1, если сопротивление движению пропорционально скорости (коэффициент пропорциональности k).
По закону Ньютона F ma; v v(t) — скорость, a dv — ускоре dt
ние. В силу F входит сила притяжения Земли и сила сопротивления воздуха.

7.1. Задачи, приводящие к дифференциальным уравнениям… |
303 |
||
Тогда |
|
||
m |
dv |
mg kvn. |
|
|
(1) |
||
|
dt |
||
Это дифференциальное уравнение 1 го порядка, т. к. в него входит первая производная.
Решение данного уравнения позволяет установить, что через неко торое время переменная скорость падения стабилизируется и стано вится почти постоянной, равной (mg k)1
k)1 n. Совершенно очевидно, что подобная задача возникает при проектировании парашютов, но не только парашютов. Аналогичное уравнение может описывать и про цесс погружения в воду, и другие жидкости.
n. Совершенно очевидно, что подобная задача возникает при проектировании парашютов, но не только парашютов. Аналогичное уравнение может описывать и про цесс погружения в воду, и другие жидкости.
П р и м е р. Шарик с отверстием нани зан на стержне и соединен с двумя пружи нами. При малых отклонениях и от положе ния равновесия закон движения груза опи сывается уравнением
и )2и.
Вновь пришли к дифференциальномуM62уравнению. Это уравнение 2 го порядка, так как оно связывает перемещение и и его вторую произ водную по времени.
Решение уравнения свободных колебаний шарика позволяет опре делить основные характеристики колебательного процесса: частоту и период колебаний. Подобные задачи возникают при разработке мно гих изделий современной техники, поскольку частота собственных (свободных) колебаний упругих элементов многих конструкций вклю чается в технический паспорт конструкции.
ОПРЕДЕЛЕНИЕ. Дифференциальным уравнением n го порядка называется уравнение вида
F(x, y, y , , y(n)) 0,
связывающее переменную x, искомую функцию y и ее производные до порядка n включительно.
7.1.2. Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет вид
F(x, y, y ) 0. (2)
Оно связывает независимую переменную x, искомую функцию y и ее производную y .

304 |
Глава 7. Обыкновенные дифференциальные уравнения |
|
|
||||
Если за уравнения (2) можно выразить y , то получим уравнение |
|
||||||
|
|
|
y f (x, y), |
|
(3) |
||
которое называется уравнением, разрешенным относительно произ |
|||||||
водной. Предположим, что правая часть уравнения (3) f (x, y) опреде |
|||||||
лена на некотором множестве А вещественной плоскости (x, y). |
|
|
|||||
ОПРЕДЕЛЕНИЕ. Функция |
y y(x), определенная на интервале |
||||||
(a, b), называется решением уравнения (3) в этом интервале, если: |
|||||||
1) |
производная y (x) x (a, b); |
|
|
|
|||
2) функция |
y y(x) обращает уравнение (3) в тождество, т. е. |
|
|||||
|
|
|
y (x) J f (x, y(x)). |
|
|
|
|
Это означает, что x (a, b) точка (x, y(x)) A. |
|
|
|
||||
Из определения следует, что решение является непрерывной на |
|||||||
всей области определения функцией. |
|
|
|
||||
Процесс нахождения решения называется интегрированием диф |
|||||||
ференциального |
уравнения. График функции |
y y(x) в декартовой |
|||||
системе координат называется интегральной кривой. |
|
|
|||||
Выясним геометрический смысл интегральной кривой. |
|
|
|||||
Пусть точка |
лежит на интегральной кривой. Так как |
|
(x) |
||||
M(x, y) |
M62 |
|
y |
||||
есть тангенс угла наклона касательной к кривой, то в точке M(x, y) |
|||||||
y (x) f (x, y) tg ). Таким образом, интегральная кривая проходит так, |
|||||||
|
|
что tg угла наклона касательной к этой кривой в |
|||||
|
|
каждой |
точке ее с координатами (x, y) |
есть |
|||
|
|
f (x, y). Пусть задано дифференциальное урав |
|||||
|
|
нение (3), где f (x, y) определена в области А на |
|||||
|
|
плоскости (x, y). В каждой точке M(x, y) этой об |
|||||
|
|
ласти проведем отрезок, составляющий с осью x |
|||||
|
Рис. 7.2 |
такой угол ), что tg ) f (x, y). Тогда говорят, |
|||||
|
|
что в области А построено поле направлений. |
|||||
|
|
Проинтегрировать дифференциальное уравне |
|||||
|
|
ние — это значит геометрически построить ин |
|||||
|
|
тегральную кривую так, чтобы направление ка |
|||||
|
|
сательной в каждой ее точке совпадало с на |
|||||
|
|
правлением отрезка поля в этой точке. |
|
|
|||
|
Рис. 7.3 |
|
Кривая, в каждой точке которой наклон |
||||
|
поля, |
определяемого |
дифференциальным |
||||
|
|
||||||
уравнением 3, один и тот же, называется изоклиной этого уравнения. |
|||||||
Уравнение изоклины имеет вид f (x, y) k const. |
|
|
|||||

7.1. Задачи, приводящие к дифференциальным уравнениям… |
305 |
П р и м е р. Рассмотрим уравнение y 2 x. Его |
|
изоклины определяются уравнением 2 x k. В ча |
|
стности, во всех точках прямой x 1 наклон поля |
|
2 |
|
равен 1, так как касательные ко всем интеграль |
|
ным кривым, пересекающим эту прямую, образу |
|
ют угол ' с положительным направлением оси OX. |
|
4 Рис. 7.4
Используя достаточно большое количество изоклин, можно получить отчетливое представление об интегральных кривых уравнения.
7.1.3. Задача Коши. Теорема Коши
Уравнение y 2 x можно проинтегрировать непосредственно: y x2 C.
Таким образом, уравнение первого порядка может иметь множество ре
шений. Для того, чтобы из множества решений выделить одно, т. е. из |
|
M62y(x0) y0. |
(4) |
семейства интегральных кривых выделить одну кривую, нужно указать точку M0, через которую эта кривая проходит. Иными словами, нужно задать значение y0, которое принимает решение y y(x) при x x0:
Задача отыскания решения y(x) уравнения (3), удовлетворяющего условию (4), называется задачей Коши. Условие (4) — начальное условие.
Однако решение задачи (3)–(4) может существовать не всегда или может быть не единственным.
Теорема Коши (теорема существования и единственности реше ния). Если правая часть f (x, y) уравнения y f (x, y) и fy(x, y) непрерыв2
ны в некоторой области А переменных x, y, то какова бы ни была внут2 ренняя точка M0(x0, y0) A, существует единственное решение y y(x)
уравнения, удовлетворяющее условию y(x0) y0.
Как это следует из теоремы Коши, через каждую точку M0(x0, y0) A при выполнении условий этой теоремы проходит единственная инте гральная кривая уравнения. Таким образом, уравнение имеет множест во решений. В рассмотренном выше примере уравнение y 2 x имело решение y x2 C для C. Чтобы из этого множества интегральных кривых выделить одну, проходящую через точку M0(x0, y0), нужно задать конкретное значение C C0 y0 x20 . Здесь y x2 C — общее решение, y x2 y0 x20 — частное решение.


7.2. Методы интегрирования некоторых дифференциальных уравнений… 307
7.2. Методы интегрирования некоторых дифференциальных уравнений первого порядка
Уравнения с разделяющимися переменными. Однородные уравнения. Линейные уравнения.
7.2.1. Уравнения с разделяющимися переменными
Уравнением с разделяющимися переменными называется уравне ние вида
dy |
f (x) f |
(y), |
|
|
|
|
|||
dx |
1 |
2 |
(1) |
|
|
|
|
||
правая часть которого представляет собой произведение двух множи телей, каждый из которых является функцией только одного аргумен та. Например, уравнение
dy |
|
sin y |
dx |
x2 x |
|
является уравнением с разделяющимисяM62переменными, а уравнение
x dy y tg x dx
таковым не является.
Перепишем уравнение (1) в виде
dy f1(x)dx. (2) f2(y)
Говорят, что в уравнении (2) переменные разделены. Предполо жим, что решение уравнения (2) найдено: y y(x). Подставив его в уравнение, получим тождество. Проинтегрируем обе части этого тож дества по x:
|
|
|
D |
dy |
D f1(x)dx C. |
|
(3) |
|||
|
|
|
f (y) |
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
(3) — общий интеграл уравнения (1). |
|
|
||||||||
З а м е ч а н и е. При |
делении на |
f2(y) мы могли потерять |
решение |
|||||||
y y0 , где f2(y0) 0. Очевидно, y y0 есть также решение уравнения (1). |
||||||||||
П р и м е р. Найти общий интеграл уравнения |
|
|||||||||
|
|
|
|
xyy 1 x2. |
|
(4) |
||||
Разделим в уравнении (4) переменные: |
|
|
||||||||
y |
dy |
|
1 x2 |
|
или |
ydy |
1 x2 |
dx. |
|
|
|
|
x |
|
|||||||
|
dx |
|
x |
|
|
|
|
|||
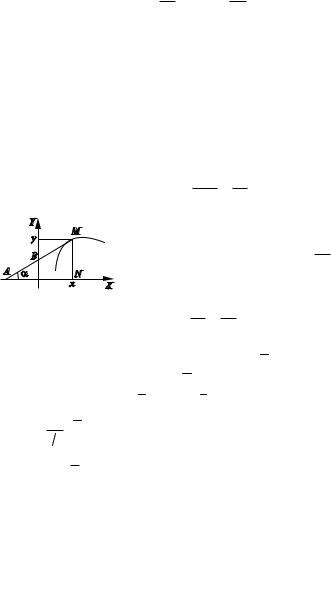

7.2.Методы интегрирования некоторых дифференциальных уравнений… 309
Пр и м е р. dy P(x, y), где P(x, y) и Q(x, y) — однородные много dx Q(x, y)
члены переменных x и y одинаковой степени однородности, т. е. такие многочлены, у которых сумма показателей степеней переменных в ка ждом члене одна и та же. Например, уравнение
dy |
|
x3 |
x2 y y3 |
dx |
|
y2 x x3 |
|
|
|
однородное, так как оба многочлена в правой части равенства имеют степень однородности 3. Действительно, это уравнение может быть приведено к виду (6)
|
|
|
|
|
|
|
|
|
y |
3 |
|
|
|
|
||
dy x3 |
x2 y y3 |
|
1 |
|
|
y |
|
|
|
|
||||||
|
x |
3 |
|
y |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
( |
|
. |
|
|
|
2 |
|
3 |
2 |
|
|
|
|
|
||||||
dx |
|
|
|
|
|
|
x |
|||||||||
|
|
|
y x |
|
x |
|
|
y |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Однородное уравнение легко преобразуется к уравнению с разде ляющимися переменными при помощи замены y z(x) или y xz. Тогда
|
dy |
|
|
dz |
|
|
|
|
x |
|
|
|
z x |
|
z x dz ((z). |
(7) |
|||||||
|
dx |
dx |
|||||||||
|
|
|
|
|
dx |
|
|
||||
Разделяя переменные, |
получим |
|
|
|
|
|
|||||
M62 |
|
|
|||||||||
|
|
|
dx |
|
|
dz |
. |
|
|
||
|
|
|
|
|
|
|
|||||
x((z) z
Тогда |
dz |
|
|
ln | x | D |
C |
||
|
|||
|
((z) z |
||
— общий интеграл уравнения (7). Найдя z z(x, C), получим y x z(x, C).
П р и м е р. Найти частное решение уравнения (x2 3y2)dx2 xydy 0, удовлетворяющее начальным условиям y 1 при x 2.
Перепишем заданное уравнение в виде |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
y 2 |
1 |
|||||||||
|
|
|
|
dy |
3y2 x2 |
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
x |
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||||
|
|
|
|
dx |
|
2 xy |
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это однородное уравнение. Полагая y zx, получим |
||||||||||||||||||||||
z x |
dz |
|
3z2 1 |
x |
dz |
|
3z2 1 |
z |
z2 1 |
. |
||||||||||||
|
|
|
|
|
||||||||||||||||||
|
dx |
|
2z |
|
|
dx |
|
|
|
2z |
|
|
|
2z |
||||||||

310 Глава 7. Обыкновенные дифференциальные уравнения
Разделим переменные: |
|
|
|
|
|
|
|
|
|||||
|
dx |
|
|
2zdz |
|
ln | x | ln | z2 1| lnC . |
|
||||||
|
|
|
|
|
|
||||||||
|
x |
|
|
z2 1 |
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
Потенцируя, получим x (z2 1) C, C /C . Вспоминая, что z |
y |
, мо |
|||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
||
жем записать: x |
|
|
1 C — общий интеграл уравнения. Исходя из |
||||||||||
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
начальных условий, найдем С. При x 2, y 1 будем иметь |
|
||||||||||||
|
|
|
|
|
2 |
1 |
|
8 |
. |
|
|
||
|
|
|
|
|
|
|
1 C |
C |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
4 |
|
3 |
|
|
|
||
Окончательно: y x 1 3 x — искомое решение.
1 3 x — искомое решение.  8
8
П р и м е р. Найти уравнение кривой, для которой отрезок, отсе каемый на оси ординат нормалью к любой точке кривой, равен рас стоянию этой точки от начала координат.
Решение. АМ — нормаль к кривой в точке M(x, y). По условию
| AO | |OM |. Уравнение нормали к кривой в точке M(x, y) имеет вид |
||||||||||
|
|
MY y 61 (X2x). |
|
|
|
(8) |
||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
Положив в (8) X 0, находим |
|
|
|
|
||||
|
|
|
|
Y y x |OA |. |
|
|
|
|
||
|
|
|
|
|
|
y |
|
|
|
|
|
|
Очевидно, |OM | |
x2 y2 . Поэтому |
|
|
|
||||
Рис. 7.6 |
|
y x x2 y2 |
y dy |
|
x |
|
. |
|||
|
y |
|
|
|
dx |
2 |
y |
2 |
y |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
||
Последнее уравнение преобразуется к виду |
|
|
|
|
||||||
|
|
dy |
|
1 |
. |
|
|
|
|
|
|
|
dx |
|
y |
2 |
y |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
Это однородное уравнение. Полагая |
y z, dy dz x z, получим |
|||||||||
|
|
|
|
|
x |
dx dx |
|
|
|
|
|
dz x z |
1 |
dz x 1 z2 . |
|
|
|
|
|||
|
dx |
|
2 |
z |
|
dx |
|
|
|
|
|
|
1 z |
|
|
|
|
|
|
||

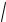





 3
3 
 3. Тогда решение уравнения имеет
3. Тогда решение уравнения имеет


 3
3