Лекции по дифференциальным уравнениям (Абрамов А.А

Теорема: Пусть '~(t) и ~(t) решения (1). Пусть '~(t1) = ~(t2). Тогда '~(t) = ~(t + t2 t1) для всех t, для которых обе части равенства определены.

Доказательство: !~(t) = ~(t+t2 t1). Тогда !~(t) решение (1), !~(t) = ~(t+t2 t1) = ~(t2) =

'~(t1).

в силу единственности решения задачи Коши.

Определение: Область G называется фазовым пространством системы дифференциальных

~

уравнений (1), графики (в G) решений фазовыми траекториями, векторы f(~y) фазовыми

скоростями. Фазовое пространство вместе с фазовыми траекториями и фазовыми скоростями, называется фазовым портретом системы дифференциальных уравнений (1).

2.Положение равновесия автономной системы дифференциальных уравнений (1)

Определение: Точка A называется положением равновесия автономной системы дифференциальных уравнений (1), если ~y(t) ~a решение (1).

84ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

3.1; 2 не вещественные, с вещественной частью, отличной от 0.

Поскольку мы хотим рисовать вещественным мелом на вещественной доске, делаем следующее: составляем вектор

1(t) = C1et sin( t + C2)2(t) = C1et cos( t + C2);

C1; C2 const.

Выкладки предлагается проделать в качестве упражнения.

Далее для определ¼нности > 0. Если оно отрицательное, поменяем местами 1; 2.

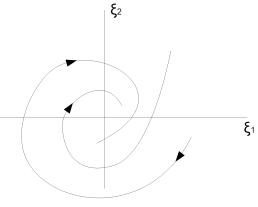
(a) < 0

Устойчивый фокус.

(b) < 0

86 ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Замечание: В книге Понтрягина детально разобраны все случаи.

2.Дополнительные замечания

1.Мы рисовали все картинки в том базисе, к которому мы перешли. В исходном базисе ~y1; ~y2, с уч¼том того, что была сделана замена переменной t, картники будут выглядеть так:

Рисуя вс¼ в исходной системе координат, надо тонко уч¼ть вс¼. что связано с переходом

в другую систему координат.

2.Мы провели классификацию, основываясь на предположениях о собственных значениях матрицы. Вопрос что называется неустойчивым узлом? Ответ в духе эти штучки касаются и расходятся , является неверным, так как это всего лишь картинка. Основой классификации является предположение о собственных значениях.

Эта классификация называется классификацией Пуанкаре линейных однородных систем дифференциальных уравнений второго порядка.

3.Все эти случаи разбиваются на два класса: 1)-3) так называемые невырожденные положения равновесия, и 4)-6) так называемые вырожденные положения равновесия.

В ч¼м смысл этого разбиения? Казалось бы, в случае 4) было получено вс¼, и выкладки являлись частным случаем случая 3). Дело в том, что каджое из невырожденных положений равновесия выделяется какими-либо условиями типа неравенства. А в определении каждого из вырожденных положений равновесия фигугирует какое-нибудь условие типа равенства.

Это важно потому что если положение равновеися невырожденное, и мы достоаточно мало меняем исходные данные, то тип положения равновесия не меняется, потому что при достаточно малом изменении исходных параметров эти значения меняются мало (непрерывные функции), а все ограничения в виде неравенств. Значит, тип невырожденного положения равновесия не меняется при достаточно малом изменении исходных параметров.

С другой стороны, для вырожденного положения равновесия это не выполняется. Центр может остаться центром, а может превратиться в фокус.

3. О нелинейных автономных системах дифференциальных уравнений

1.Мы рассматриваем общую нелинейную систему

~

A = @@~fy (~a); j~g(~z)j = o(j~zj).

(1) , (2).

Определение: (3) получено из (1) линеаризацией в окрестности положения равновесия ~a.

Один из основных при¼мов исследования поведения решений: прежде всего изучаем уравнение

(3), и выясняем нужные нам свойства на этом уравнении, затем стараемся перенести эти результаты на уравнение (2).

2.Пусть n = 2. (Линейная автономная система второго порядка).

Имеет место следующий нетривиально доказываемый факт:

Траектории уравнения (1) в окрестности положения равновесия ведут себя , если положения равновесия системы (3) невырожденное, качественно так же, как и траектории уравнения (3).

90 ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Выберем так, чтобы ~ + Q < 0. (Чтобы отрицательное число ~ мало сдвинулось вправо.) Для этого надо взять соответствующее . Теперь взяли ~, обладающее таким свойством:

Q~ < , ~ < .

Начальные значения подчиняются условию:

Если для 0 6 6 t решение ~z(t) определено, имеет место j~zj 6 и выполняется условие (4), то

Сейчас мы докажем, что решение действительно определено, прич¼м для всех t, и для всех решений ~z не выходит за указанные пределы. (Иначе говоря, эти предположения выполняются).

Возьм¼м цилиндр S, такой, что

S : f0 6 t < +1; j~zj 6 g

Задача Коши с такими начальными данными имеет решение. Теперь докажем, что оно не выходит за пределы цилиндра.

Теорема доказана.

Замечание: Докажите, что если хотя бы одно собственное значение матрицы лежит в правой полуплоскости, то решение не является устойчивым по Ляпунову. Подсказка: ограничиться случаем уравнения (3).